Most
of the observable universe consists of plasma, or partially ionized
gas. The processes of ionization and their sources of energy are
regarded as one of the important open questions in astrophysics.
According to Newton’s theory, the gravitational force between a
proton and an electron is weaker than the electromagnetic force
between them by a factor of about
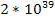 .
For this reason, the influence of gravitation on the atomic scale,
specifically its ability to ionize an atom, is assumed to be
non-existent. Furthermore, according to Newtonian dynamics, the
gravitational acceleration of a particle is independent of its mass,
a belief that led to Einstein’s principle of equivalence.
Consequently, under Newton’s theory of gravitation and general
relativity, free falling protons, electrons and neutrons are expected
to accelerate at the exact same rate. Therefore, the ionization of
atoms is extremely unlikely to be caused by the gravitational force.1
Rather, current theories attribute ionization to either a thermal
process or to strong electromagnetic fields. .
For this reason, the influence of gravitation on the atomic scale,
specifically its ability to ionize an atom, is assumed to be
non-existent. Furthermore, according to Newtonian dynamics, the
gravitational acceleration of a particle is independent of its mass,
a belief that led to Einstein’s principle of equivalence.
Consequently, under Newton’s theory of gravitation and general
relativity, free falling protons, electrons and neutrons are expected
to accelerate at the exact same rate. Therefore, the ionization of
atoms is extremely unlikely to be caused by the gravitational force.1
Rather, current theories attribute ionization to either a thermal
process or to strong electromagnetic fields.
However, massive
ionization by the gravitational force alone is predicted and
explained by the UG theory, even at distances of
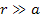 ,
where the exponent ,
where the exponent
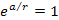 .
According to equation 2-1-2, at distances of .
According to equation 2-1-2, at distances of
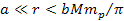 ,
the UG gravitational force between a superheavy particle of mass ,
the UG gravitational force between a superheavy particle of mass
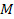 and a nucleon of mass
and a nucleon of mass
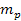 is greater than the equivalent Newtonian force by an order of
is greater than the equivalent Newtonian force by an order of
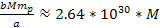 ,
and is thus capable of exceeding the electromagnetic force between an
electron and a proton, given a sufficiently large SHP mass. 23
In addition, the acceleration of a proton by a superheavy particle
of mass ,
and is thus capable of exceeding the electromagnetic force between an
electron and a proton, given a sufficiently large SHP mass. 23
In addition, the acceleration of a proton by a superheavy particle
of mass
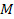 from a distance
from a distance
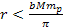 is expected to vary from the acceleration of an electron from the
same distance.
is expected to vary from the acceleration of an electron from the
same distance. Consider the
simpler case of a hydrogen atom
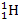 encircling the center of a star or galaxy dominated by a single SHP
type of mass M surrounded by ordinary matter. To simplify the
analysis, the velocity
encircling the center of a star or galaxy dominated by a single SHP
type of mass M surrounded by ordinary matter. To simplify the
analysis, the velocity
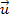 of the atom relative to the superheavy particle is assumed to be
non-relativistic. The energy of the atom is thus given by
of the atom relative to the superheavy particle is assumed to be
non-relativistic. The energy of the atom is thus given by Equation
8-1 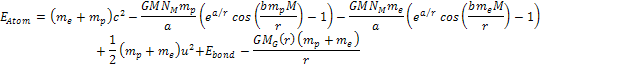
where
the atom is assumed to rotate in a circular orbit of radius
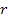 around a group of
around a group of
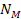 SHPs of particle mass
SHPs of particle mass
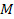 concentrated in a small sphere of a radius that is negligible
relative to
concentrated in a small sphere of a radius that is negligible
relative to
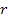 .
The sphere of superheavy particles is assumed to be surrounded by a
spherically symmetric distribution of ordinary matter of mass .
The sphere of superheavy particles is assumed to be surrounded by a
spherically symmetric distribution of ordinary matter of mass
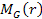 .
The electron-proton bonding energy of a free atom .
The electron-proton bonding energy of a free atom
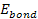 must be negative, where at the ground state of the hydrogen atom,
must be negative, where at the ground state of the hydrogen atom,
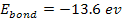 .4
Note that only the terms .4
Note that only the terms
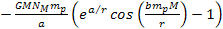 and
and
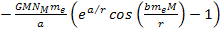 in equation 8-1 are non-linear functions of the proton and electron
masses, and are therefore the only terms capable of generating a
differential force that can separate the electron from the proton to
ionize the atom.
in equation 8-1 are non-linear functions of the proton and electron
masses, and are therefore the only terms capable of generating a
differential force that can separate the electron from the proton to
ionize the atom.
The orbiting atom gravitates toward the potential energy minima
generated by its interaction with the galactic superheavy particles
and ordinary matter. The magnitudes and locations of the zonal
oscillation maxima and minima of both the proton and the electron due
to the dominant
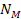 SHPs of mass
SHPs of mass
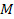 can be derived via equations 2-1-1 and 2-1-42 respectively. Since
the proton and the electron are independent particles of vastly
different masses, their interactions with the superheavy particles
generate distinct sets of potential energy minima. As the zonal
oscillation range of the SHP-proton pair is proportional to
can be derived via equations 2-1-1 and 2-1-42 respectively. Since
the proton and the electron are independent particles of vastly
different masses, their interactions with the superheavy particles
generate distinct sets of potential energy minima. As the zonal
oscillation range of the SHP-proton pair is proportional to
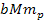 ,
and the zonal oscillation range of the SHP-electron pair is
proportional to ,
and the zonal oscillation range of the SHP-electron pair is
proportional to
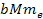 ,
the radius of the proton’s zonal oscillation range is about
1,836 times greater than that of the electron. ,
the radius of the proton’s zonal oscillation range is about
1,836 times greater than that of the electron.
The characteristics of the interaction between the atom and the
central superheavy particles can be viewed at three different
distance ranges. At distances
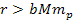 ,
the UG potential energy of the proton and the electron approach their
Newtonian form, and the differential gravitational force (as well as
the total gravitational force) applied on the proton and the
electron is negligible relative to the electromagnetic force between
them. Therefore, the hydrogen atom remains intact. ,
the UG potential energy of the proton and the electron approach their
Newtonian form, and the differential gravitational force (as well as
the total gravitational force) applied on the proton and the
electron is negligible relative to the electromagnetic force between
them. Therefore, the hydrogen atom remains intact.
At distances
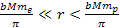 ,
the UG force applied on the electron is still Newtonian, and
therefore negligible. However, the protons (as well as neutrons) are
within their zonal oscillation range with the SHPs and are attracted
toward their nearest minimum ,
the UG force applied on the electron is still Newtonian, and
therefore negligible. However, the protons (as well as neutrons) are
within their zonal oscillation range with the SHPs and are attracted
toward their nearest minimum
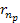 .5
Consequently, free protons, atoms, molecules and ions are drawn
toward the nearest .5
Consequently, free protons, atoms, molecules and ions are drawn
toward the nearest
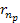 minimum. As the UG force applied on the electron at this range of
distances is negligible, the electron will remain bonded to the
proton by the electromagnetic force.
minimum. As the UG force applied on the electron at this range of
distances is negligible, the electron will remain bonded to the
proton by the electromagnetic force.
Note that since
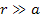 ,
the potential energy of the proton is given by ,
the potential energy of the proton is given by
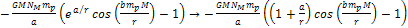 ,
and the minima occur where ,
and the minima occur where
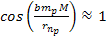 .
At these minima the potential energy is approximately .
At these minima the potential energy is approximately
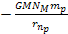 ,
which is equal to Newton’s gravitational potential energy.
Consequently, the atoms will assume circular Newtonian orbits.
However, in contrast to Newton’s theory, only a discreet (or
quantized) set of orbits at close proximity to the minima are
allowed. ,
which is equal to Newton’s gravitational potential energy.
Consequently, the atoms will assume circular Newtonian orbits.
However, in contrast to Newton’s theory, only a discreet (or
quantized) set of orbits at close proximity to the minima are
allowed.
At distances
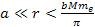 ,
the electrons, as well as the protons and neutrons, are situated
within their SHP zonal oscillation range. As the electron mass is
about 1,836 times lighter than the mass of the protons (or
neutrons), all protons, atoms, ions and molecules are attracted
toward the nearest minimum of the proton’s set of minima ,
the electrons, as well as the protons and neutrons, are situated
within their SHP zonal oscillation range. As the electron mass is
about 1,836 times lighter than the mass of the protons (or
neutrons), all protons, atoms, ions and molecules are attracted
toward the nearest minimum of the proton’s set of minima
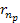 .
As long as the differential UG force between the hydrogen’s
proton and electron is smaller than the electromagnetic force which
bonds them, the atom is likely to remain intact, and the electron is
forced to follow the heavier proton and to gravitate toward the
potential energy minima of the proton. The locations of these minima
can be derived using equation 2-1-42. For the case where .
As long as the differential UG force between the hydrogen’s
proton and electron is smaller than the electromagnetic force which
bonds them, the atom is likely to remain intact, and the electron is
forced to follow the heavier proton and to gravitate toward the
potential energy minima of the proton. The locations of these minima
can be derived using equation 2-1-42. For the case where
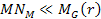 and
and
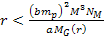 ,
the energy minima of the proton and the electron occur at ,
the energy minima of the proton and the electron occur at Equation
8-2a 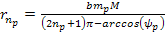
where
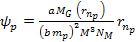 and
and
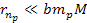 ,
or ,
or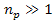 .
Thus, .
Thus,
Equation
8-2b
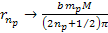 as
as
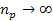
where
minima occur at any integer 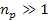 ,
and where ,
and where 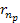 of equation 8-2b fulfills
of equation 8-2b fulfills 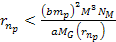 and
and 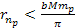 .
Similarly, the electrons are drawn by the UG force toward their own
minima at approximately .
Similarly, the electrons are drawn by the UG force toward their own
minima at approximately Equation
8-2c
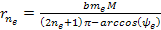
where
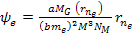 and
and
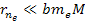 ,
or ,
or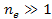 ,
or ,
or
Equation
8-2d 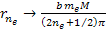 as
as
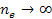
where minima occur at any integer
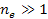 . .
Since
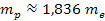 ,
there are ,
there are
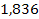 proton potential energy minima at distances greater than the first
minimum of the SHP-electron UG interaction, and there are 1,836
proton potential energy minima between any two successive minimum
contours of the electron.
proton potential energy minima at distances greater than the first
minimum of the SHP-electron UG interaction, and there are 1,836
proton potential energy minima between any two successive minimum
contours of the electron.
According to equation 2-1-2, the UG force steering the electron
toward its closest potential energy minimum is approximately
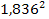 times
smaller than the force acting on the proton. Therefore, the atom
settles in the immediate vicinity of the proton’s potential
energy minimum, and in the case of a weak local UG gravitational
influence, the electron is prevented from approaching its own
potential energy minimum by the electromagnetic force that bonds it
to the proton. Since there are approximately 1,836 proton potential
energy minima between any two successive electron potential energy
minima, most of the electrons that are bonded to orbiting hydrogen
atoms demonstrate orbital radii that deviate significantly from the
radii of their UG minima. It will be shown that at some of these
minima, the overall stability of the proton-electron system may
increase due to the ionization of the hydrogen atom, while the
barrier threshold of the ionization is either too small or
non-existent, and therefore cannot prevent massive ionization. An
atom is likely to be ionized at a given location if its overall
energy is higher than the total sum of the energies of the ion and
its displaced electron, where the electron’s amount of
displacement times
smaller than the force acting on the proton. Therefore, the atom
settles in the immediate vicinity of the proton’s potential
energy minimum, and in the case of a weak local UG gravitational
influence, the electron is prevented from approaching its own
potential energy minimum by the electromagnetic force that bonds it
to the proton. Since there are approximately 1,836 proton potential
energy minima between any two successive electron potential energy
minima, most of the electrons that are bonded to orbiting hydrogen
atoms demonstrate orbital radii that deviate significantly from the
radii of their UG minima. It will be shown that at some of these
minima, the overall stability of the proton-electron system may
increase due to the ionization of the hydrogen atom, while the
barrier threshold of the ionization is either too small or
non-existent, and therefore cannot prevent massive ionization. An
atom is likely to be ionized at a given location if its overall
energy is higher than the total sum of the energies of the ion and
its displaced electron, where the electron’s amount of
displacement
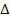 is larger than, but of the same order of magnitude as the Bohr
radius. For massive ionization to occur, the following equation must
hold true at the radius where ionization takes place:6
is larger than, but of the same order of magnitude as the Bohr
radius. For massive ionization to occur, the following equation must
hold true at the radius where ionization takes place:6 Equation
8-3 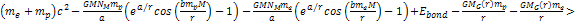
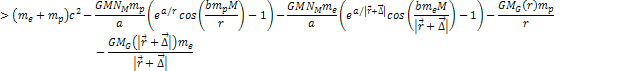
where
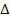 is of the order of the radius of the hydrogen atom.
Note that the loss of the electron
has virtually no significant effect on the location of the ion (in
this case, a proton), as
is of the order of the radius of the hydrogen atom.
Note that the loss of the electron
has virtually no significant effect on the location of the ion (in
this case, a proton), as 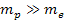 .
Also note that since .
Also note that since 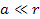 , ,
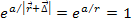 .
Therefore, massive ionization
will take place when .
Therefore, massive ionization
will take place when Equation
8-4
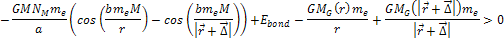
With
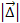 of the order of the Bohr radius, the term
of the order of the Bohr radius, the term
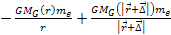 is negligible relative to
is negligible relative to
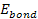 .
Using the trigonometric equation .
Using the trigonometric equation 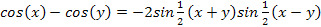 , ,
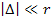 ,
and ,
and
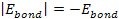 results in massive ionization occurring when
results in massive ionization occurring when
Equation
8-5
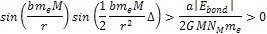
As
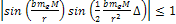 ,
massive ionization can happen only if ,
massive ionization can happen only if
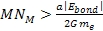 .
Therefore, massive ionization of hydrogen atoms at their ground
state, where .
Therefore, massive ionization of hydrogen atoms at their ground
state, where
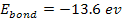 ,
can occur only when ,
can occur only when
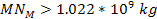 . .
The gravitational ionization of other atoms or molecules can be
treated similarly. Atomic ionization energy ranges between
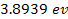 (for cesium) and
(for cesium) and
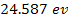 (for helium). Therefore, massive atomic ionization at
(for helium). Therefore, massive atomic ionization at
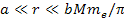 requires the total mass of the dominant SHP in the present
scenario to be at least requires the total mass of the dominant SHP in the present
scenario to be at least
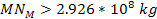 .7
Note that via equation 8-5, the removal of the last electron from
the ground state of an atom with .7
Note that via equation 8-5, the removal of the last electron from
the ground state of an atom with
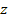 protons will require approximately
protons will require approximately
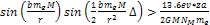 . . The
above discussion reveals two key concepts. First, a substantial
portion of the massive amount of plasma detected in the universe may
be produced via gravitational ionization. Second, the electrons
freed by ionization settle into entirely different orbits than the
orbits of ions or atoms.8
In the following chapter, this phenomenon will be shown to explain
the generation of the magnetic fields created by planets, stars and
galaxies, and may be instrumental in understanding the observed
phenomena of jets and pulsars.
1 An exception to this statement
is when extremely strong tidal forces exist. For sufficiently
strong tidal forces to occur over distances of the order of the
diameter of an atom, the gradients of Newton’s
gravitational force must
be enormous. Such gradients are theoretically possible within black
holes. However, in order to experience such enormous gravitational
tidal forces in the general relativity scenario, the atom must cross
the black hole event horizon.
In such a case, the ejected electrons
must remain trapped within the black
hole and cannot be detected by an outside observer, as even light
cannot escape. Therefore, this process cannot produce any
observable ionization. 2
This value was calculated using 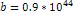 , ,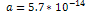 and and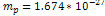 . . 3
Following the non-relativistic force equation 2-1-2, 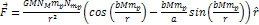 ,
the oscillation amplitude of the cosine term is negligible relative
to the amplitude of the term ,
the oscillation amplitude of the cosine term is negligible relative
to the amplitude of the term 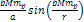 .
Therefore, at the maxima the UG force becomes larger than the
Newtonian force by a factor of .
Therefore, at the maxima the UG force becomes larger than the
Newtonian force by a factor of 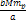 . . 4
The ionization energies
of the other energy states of the hydrogen atom,
are roughly equal to 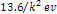 ,
where ,
where 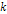 is an integer greater than zero.
is an integer greater than zero. 5
For simplicity, the small difference between the mass of the proton
and the neutron can be neglected. 6
Note that due to a quantum tunneling effect, ionization
may also occur when the overall energy is increased due to
ionization. However, in such a case the ionization rate would be
low, and massive ionization would not occur. 7
Lower 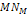 values may be sufficient to ionize some large molecules, which may
lower ionization energy.
values may be sufficient to ionize some large molecules, which may
lower ionization energy. 8
Note that in the first order of approximation, where the masses of
the protons and neutrons
are assumed to be equal and the mass of the bonded electrons
is assumed to be negligible relative to the mass of protons,
all ions, atoms and molecules share the same orbits. For a
sufficiently large 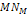 ,
these orbits may split into a series of nearby sub-orbits. For
example, different isotopes of the same atom may demonstrate
slightly different radii of orbit, or the orbital radius of an ion
of a given element may differ slightly from the orbital radius of an
atom of the same element. ,
these orbits may split into a series of nearby sub-orbits. For
example, different isotopes of the same atom may demonstrate
slightly different radii of orbit, or the orbital radius of an ion
of a given element may differ slightly from the orbital radius of an
atom of the same element.
|



