It
has been nearly four hundred years since Galileo first observed
Saturnís extensive ring system, and about 20 to 30 years since
smaller ring systems were discovered around Jupiter, Uranus and
Neptune. Despite the extensive study of planetary rings and major
improvements in theory, as more detailed measurements become
available, observations reveal increasingly complex systems, and many
features within the rings have not yet been adequately explained.1
Current theories explaining the observed planetary ring structures
for the most part describe gravitational interactions between ring
material, nearby satellites and the parent planet. As the mass of
each of the four solar gas planets exceeds the mass of their
respective satellites by several orders of magnitude, the planetary
influence on the behavior of ring particles is likely to be far
greater than that of the satellites. When applied to an isolated
planet-ring system (without the influence of nearby satellites),
Newtonís theory of gravitation allows a rotating object to
occupy one of an infinite number of possible Keplarian orbits,
however does not maintain any intrinsic preference for one orbit over
another. Hence, an elaborate ring structure, as observed in the
Saturnian system, is unlikely to be explained simply by Newtonís
predicted gravitational interaction between ring particles and their
parent planet. Such structure, even if formed, would be expected to
decay over time. Current theories thus mainly center on orbital
resonances between ring particles and satellites as the possible
underlying cause for the planetary ring structure.
Large bodies cannot form spontaneously at orbital radii below the
Roche limit of a planet, where the tidal forces acting on different
portions of the bodies become stronger than the gravitational force
that acts between them to keep them intact. Therefore, satellites
may form spontaneously only at radii exceeding their planetís
Roche limit. In all four gas planets, the number of satellites
decreases outside of the Roche limit, while their size and the space
between them increase with distance from the planet. As the orbits
of the planetary satellites and ring matter are Keplerian, their
orbital periods change continuously with distance from the planet,
and their speeds reduce proportionally to
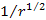 .
Therefore, there are a large yet countable number of radii where the
orbital period of the ring particles is a simple integer fraction of
a given satelliteís orbital period, referred to as an orbital
resonance. At ring distances at which orbital resonances do not
occur, the location of the closest encounter between the satellite
and the ring particle varies and the average satelliteís
influence on the ring particle tends to cancel out over time.
However, as a result of orbital resonances, periodic close encounters
occur at fixed locations and the small gravitational forces from the
satellite repeatedly act on the same ring material. After some number
of orbits this may cause a notable disturbance.2
The migration of material away from the radii of the resonances is
believed to explain some of the gaps within the rings. In certain
cases, a gap may be produced by an embedded satellite that is large
enough to clear a space in the ring, as in the case of the moons,
Pan and Daphnis, respectively located within the Encke and Keeler
gaps in Saturnís ring system. A mechanism by which the gravity
of a local moonlet, or shepherd moon, pushes ring material away was
also thought to explain how narrow ringlets are confined and
prevented from spreading out.3 .
Therefore, there are a large yet countable number of radii where the
orbital period of the ring particles is a simple integer fraction of
a given satelliteís orbital period, referred to as an orbital
resonance. At ring distances at which orbital resonances do not
occur, the location of the closest encounter between the satellite
and the ring particle varies and the average satelliteís
influence on the ring particle tends to cancel out over time.
However, as a result of orbital resonances, periodic close encounters
occur at fixed locations and the small gravitational forces from the
satellite repeatedly act on the same ring material. After some number
of orbits this may cause a notable disturbance.2
The migration of material away from the radii of the resonances is
believed to explain some of the gaps within the rings. In certain
cases, a gap may be produced by an embedded satellite that is large
enough to clear a space in the ring, as in the case of the moons,
Pan and Daphnis, respectively located within the Encke and Keeler
gaps in Saturnís ring system. A mechanism by which the gravity
of a local moonlet, or shepherd moon, pushes ring material away was
also thought to explain how narrow ringlets are confined and
prevented from spreading out.3
Although the current Newtonian-based theories have been successful in
accounting for a small number of planetary rings and gaps, a broad
and conclusive theory has not yet been developed to explain the
structure and vastness of the known ring systems, or their specific
patterns. The relatively simpler ring systems of Jupiter, Uranus and
Neptune are far from being understood, however they present far less
of a challenge than the A and B rings of Saturn, where the origin of
the rings and their unique properties are still unknown. Explanation
of certain A and B ring characteristics via orbital resonances
requires an enormous amount of embedded satellites, all less than a
kilometer in diameter.4
Even then, the cause of the irregular structure of the inner half of
the B ring remains unaccounted for. In the case of Uranusís
less extensive ring system, none of the known satellites provide the
gravitational forces needed to confine its ring particles. A
thorough search to locate satellites closer to the planet than
Cordelia restricts the possible size of satellites to be too small to
effectively shape and confine the Uranian rings via gravitational
shepherding.5
Further questions address the mechanisms that determine the
sharpness and ellipticity of planetary rings. It is unclear why some
rings are sharp and narrow while others are wide and diffused, or why
some of the rings are more elliptical than others, or what causes the
formation of arcs. There are also questions as to how the planetary
ring and satellite systems were created, their ages, and how they
persist and change over time. According to current theories, rings
can essentially form in two ways: (1) Planetary rings may be a
remnant of material from the distant past of a planet that was
prevented from coalescing into individual satellites, or (2) ring
material may be comprised of the remaining debris of former
satellites that wandered too close to the planet and were torn apart
by its gravitational tides, or of satellites shattered by collision
with an interplanetary object. Certain rings may also be replenished
by meteoroid bombardment, or by eruptions from a nearby satellite.6
When applied to the estimated timescale of the rings, data from
NASAís Voyager Spacecraft in the 1970s, and later from NASAís
Hubble Space Telescope, led scientists to infer that Saturnís
present rings could not have existed for more than tens of millions
of years, a small fraction of the age of the Solar System. Planetary
rings were thus believed to be a temporary feature created by some
cataclysmic event(s) and expected to dissipate over time. However, it
is very difficult to understand how such a massive ring system as
Saturnís could be so finely divided by those same processes
over time periods lasting only tens, or at most hundreds of millions
of years, especially when an interplanetary meteoroid flux is thought
to have been almost depleted for a much longer period of time.
Features observed by NASAís Cassini mission indicate that
Saturnís finely divided rings could not have resulted from a
single cataclysmic event, and instead may persist through a recycling
of material. Observations show that even when ring objects fragment
into groups of smaller particles, they tend to re-clump together to
sustain the overall ring structure. Support is subsequently
escalating for the theory that the Saturnian ring system formed with
the creation of the planet and Solar System, in contradiction to many
existing theories.7
Finally, current theories that explain the structure of ring
systems via interactions between their ring particles and satellites
do not address questions as to why gas planets have a large number of
satellites, or why those satellites rotate at their specific orbital
locations. Careful analysis of the orbital periods of satellites
reveals that the resonances that occur between rings are of the same
kinds that occur between satellites and rings, or between different
satellites. This strongly suggests that satellites and rings were
formed from the same material via the same mechanism. It is proposed
by the UG theory that planetary satellites follow the same orbits
previously occupied by former rings. This view is further
strengthened by the observation that both Saturn and Uranus have
rings and satellites that share the same orbits. Therefore, we are
left with the classic chicken and egg question: which came first, the
rings which formed the satellites or the satellites which formed the
rings?
Although Newtonís theory of gravitation (as well as general
relativity) has been repeatedly tested and proven to work well in our
Solar System, a four hundred year old question, which is older than
the Newtonian theory itself, regarding the origin and the mechanisms
underlying Saturnís ring structure remains unsolved. This
query will be evaluated via a UG analysis of the Saturnian ring
system. The present goal, however, is to demonstrate the power of
the UG theory and its ability to provide the general morphology and
characteristics of complex systems on all distance scales. Therefore,
the current UG analysis of planetary rings will be limited to
Saturnís main body of rings, specifically rings D, C, B, A and
the Cassini Division. Nevertheless, the same methods and techniques
used here may be applied to the remaining planetary ring systems.
Section
V-2: The D, C, B, A, and F Rings and the Cassini Division
of Saturn
Following equation 3-3-1 developed in chapter III-3, the velocity of
the SHP groups in orbit around the center of an astronomical body is
given by Equation
5-1 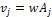
where
the following rules must be fulfilled: Rule 1: In a steady state condition, all orbiting SHP groups with a
zonal oscillation range exceeding their orbital radius
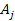 around the center of an astronomical body share the same angular
velocity
around the center of an astronomical body share the same angular
velocity
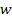 ,
where ,
where
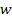 is the angular velocity of the central core of the astronomical body.
is the angular velocity of the central core of the astronomical body.
Rule 2: As a consequence of equation 5-1, and the requirement that
the velocity of a superheavy particle cannot surpass the speed of
light, all superheavy particles with a zonal oscillation range
greater than
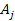 must reside within the distance
must reside within the distance
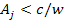 from the center.
from the center. A
direct consequence of equation 5-1 is that the velocity of a
superheavy particle of mass
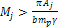 is relativistic when
is relativistic when
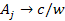 .8
According to the theory developed in Chapter III (and demonstrated
for galaxies in chapter IV), the existence of wide rings and
extensive spiral structure requires some SHP groups to orbit at
relativistic speeds.9
Hence, achieving the vast and almost continuous spread of Saturnís
main body of rings requires that some of its SHP groups rotate at
relativistic velocities. However, the surface matter of the planet
rotates at far below relativistic speeds. This leads to the
conclusion that Saturnís central core must rotate at a far
greater angular velocity than the planetary surface. In the contrary
case, if Saturnís central core, and therefore its relativistic
SHP groups, travel at an angular velocity lower than or equal to the
angular velocity of the planetís surface, the orbital radii of
the relativistic SHP groups would need to exceed the radius of the
planet by several orders of magnitude, resulting in an entirely
different structure than observed. As discussed in Chapter IV,
ordinary matter accumulates to form rings or spirals in the vicinity
of the deep minima contours created by the interaction between the
dominant, centrally located SHP groups and ordinary matter.10
In the case of stationary superheavy particles (or low SHP
velocities), the density of the ordinary matter is expected to
increase in the vicinity of the resultant stationary (or low
velocity) zonal minima. For the case where the angular velocity of
the SHP groups exceeds the angular velocity of the orbiting object,
the SHP-generated minima move faster than the ability of the object
to follow. Thus, a higher density of ordinary matter can be expected
at the minima of the average potential energy, where the average
potential energy is calculated over a period of time equal to .8
According to the theory developed in Chapter III (and demonstrated
for galaxies in chapter IV), the existence of wide rings and
extensive spiral structure requires some SHP groups to orbit at
relativistic speeds.9
Hence, achieving the vast and almost continuous spread of Saturnís
main body of rings requires that some of its SHP groups rotate at
relativistic velocities. However, the surface matter of the planet
rotates at far below relativistic speeds. This leads to the
conclusion that Saturnís central core must rotate at a far
greater angular velocity than the planetary surface. In the contrary
case, if Saturnís central core, and therefore its relativistic
SHP groups, travel at an angular velocity lower than or equal to the
angular velocity of the planetís surface, the orbital radii of
the relativistic SHP groups would need to exceed the radius of the
planet by several orders of magnitude, resulting in an entirely
different structure than observed. As discussed in Chapter IV,
ordinary matter accumulates to form rings or spirals in the vicinity
of the deep minima contours created by the interaction between the
dominant, centrally located SHP groups and ordinary matter.10
In the case of stationary superheavy particles (or low SHP
velocities), the density of the ordinary matter is expected to
increase in the vicinity of the resultant stationary (or low
velocity) zonal minima. For the case where the angular velocity of
the SHP groups exceeds the angular velocity of the orbiting object,
the SHP-generated minima move faster than the ability of the object
to follow. Thus, a higher density of ordinary matter can be expected
at the minima of the average potential energy, where the average
potential energy is calculated over a period of time equal to
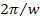 seconds. In areas where the density of ordinary matter is
sufficiently high and the gravitational tidal forces are not too
strong, ring matter will begin to coalesce into satellites or other
relatively large objects. As the UG equations of motion have a
linear dependency on the number of particles involved, and the
process of coalescence is assumed to simply ďglueĒ
particles together while conserving their types and their numbers,
the orbit of a newly constructed object should be approximately equal
to the average of the prior orbits of its individual particles.
Furthermore, as the velocities of Saturnís satellites and ring
matter are observed to obey Keplerian dynamics, the angular velocity
of the newly created object is expected to be slightly higher than
the angular velocities of adjacent particles at larger orbital radii,
and lower than the angular velocities of adjacent particles at
smaller orbital radii. In either case, the rotating object will
periodically encounter nearby orbiting matter. Over time the
gravitational pull of the object, which is magnified by the
accumulating effect of many synchronized periodic encounters, causes
a disturbance and a shift in the orbits of surrounding matter.
Adjacent orbiting matter may consequently be absorbed into the
forming object, or expelled away from their initial orbital
locations, creating a small gap around the objectís orbit. As
the mass of the object increases, its gravitational reach expands,
allowing for the consumption or ejection of material from a larger
range of distances, consequently widening the gap. The mass of the
object and the size of the gap continue to grow as long as there is
an available supply of matter in the vicinity of the object, and as
long as the entire object is located beyond the planetís Roche
limit.11
seconds. In areas where the density of ordinary matter is
sufficiently high and the gravitational tidal forces are not too
strong, ring matter will begin to coalesce into satellites or other
relatively large objects. As the UG equations of motion have a
linear dependency on the number of particles involved, and the
process of coalescence is assumed to simply ďglueĒ
particles together while conserving their types and their numbers,
the orbit of a newly constructed object should be approximately equal
to the average of the prior orbits of its individual particles.
Furthermore, as the velocities of Saturnís satellites and ring
matter are observed to obey Keplerian dynamics, the angular velocity
of the newly created object is expected to be slightly higher than
the angular velocities of adjacent particles at larger orbital radii,
and lower than the angular velocities of adjacent particles at
smaller orbital radii. In either case, the rotating object will
periodically encounter nearby orbiting matter. Over time the
gravitational pull of the object, which is magnified by the
accumulating effect of many synchronized periodic encounters, causes
a disturbance and a shift in the orbits of surrounding matter.
Adjacent orbiting matter may consequently be absorbed into the
forming object, or expelled away from their initial orbital
locations, creating a small gap around the objectís orbit. As
the mass of the object increases, its gravitational reach expands,
allowing for the consumption or ejection of material from a larger
range of distances, consequently widening the gap. The mass of the
object and the size of the gap continue to grow as long as there is
an available supply of matter in the vicinity of the object, and as
long as the entire object is located beyond the planetís Roche
limit.11 The
strength of a theory is determined by its ability to explain all
observed phenomena using a minimal number of variables and
assumptions, as well as its ability to correctly predict the outcome
of new experiments. The goal of the current exercise is to
demonstrate the ability of the UG theory to explain the observed
structure of Saturnís main body of rings, specifically rings D,
C, B, A, F and the Cassini Division, using a simple model of very few
variables. As discussed, a UG-based model that is capable of
explaining a vast and complicated structure such as Saturnís
ring system requires superheavy particles orbiting at relativistic
velocities. The simplest possible UG model that fulfills this
requirement consists of a single SHP group with
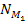 superheavy particles of particle mass
superheavy particles of particle mass
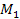 rotating at a speed of
rotating at a speed of
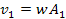 in a circular orbit of radius
in a circular orbit of radius
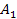 around the planetary center (using a total of five independent
parameters
around the planetary center (using a total of five independent
parameters
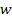 , ,
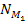 , ,
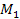 , ,
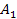 ,
and ,
and
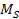 ,
where ,
where
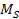 denotes the overall mass of Saturnís ordinary matter). This
simple model will be demonstrated to successfully explain the general
structure of the Saturnian ring system, as well as a number of
principal ring characteristics. In particular, the model will address
the origin and stability of the current ring structure, spiral wave
patterns within the rings,12
the observed dynamic changes in structure occurring over time, and
the phenomenon of spokes.
denotes the overall mass of Saturnís ordinary matter). This
simple model will be demonstrated to successfully explain the general
structure of the Saturnian ring system, as well as a number of
principal ring characteristics. In particular, the model will address
the origin and stability of the current ring structure, spiral wave
patterns within the rings,12
the observed dynamic changes in structure occurring over time, and
the phenomenon of spokes.
While successful in explaining the general ring structure down to a
scale of a few hundred kilometers, the simplified model does not
produce the observed fine structure of Saturnís rings.
Resolving this issue thus requires the addition of at least one more
SHP group. To keep the complexity of the model to a minimum, a
second group of
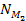 SHPs of the same mass
SHPs of the same mass
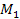 rotating at a velocity of
rotating at a velocity of
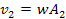 around the center of the planet in a circular orbit of radius
around the center of the planet in a circular orbit of radius
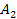 can be added, increasing the total number of independent variables to
seven. In this example the variables
can be added, increasing the total number of independent variables to
seven. In this example the variables
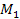 , ,
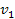 , ,
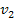 , ,
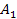 , ,
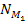 , ,
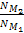 and
and
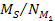 were selected. For simplicity,
were selected. For simplicity,
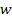 was replaced by
was replaced by
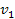 ,
where ,
where
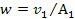 ,
and ,
and
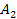 was replaced by
was replaced by
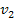 ,
where ,
where
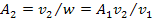 .13
The above analysis will be shown to produce a fairly accurate model
of the general structure as well as the underlying fine-scale
structure of Saturnís main body of rings. .13
The above analysis will be shown to produce a fairly accurate model
of the general structure as well as the underlying fine-scale
structure of Saturnís main body of rings.
An initial rough estimation of the mass of the superheavy particle
that dominates the structure of Saturnís ring system can be
deduced from the characteristics of the outermost E ring, extending
from about
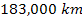 to beyond
to beyond
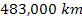 from the planetary center. As the E ring provides the observed
external boundary of Saturnís rings, it can be assumed to
reside in the vicinity of the outermost maximum contour of the SHP
group that dominates within the range of
from the planetary center. As the E ring provides the observed
external boundary of Saturnís rings, it can be assumed to
reside in the vicinity of the outermost maximum contour of the SHP
group that dominates within the range of
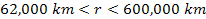 .
Consequently, it is reasonable to assume that the outer maximum
associated with the dominant SHP occurs somewhere between about .
Consequently, it is reasonable to assume that the outer maximum
associated with the dominant SHP occurs somewhere between about
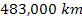 and
and
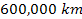 from the planetary center. Using the non-relativistic equation
2-1-42, the external maximum is given by
from the planetary center. Using the non-relativistic equation
2-1-42, the external maximum is given by
Equation
5-2 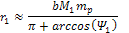
where
Saturnís entire collection of ordinary matter and remaining
superheavy particles (other than those of group
 )
influences the location of this maximum exclusively through the term )
influences the location of this maximum exclusively through the term
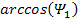 ,
where ,
where
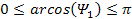 and
and
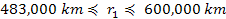 .
Substituting these inequalities into equation 5-2, where the
denominator of the equation is between .
Substituting these inequalities into equation 5-2, where the
denominator of the equation is between
 and and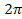 ,
yields ,
yields
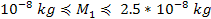 .
To further narrow down the values of the dominant SHP group
responsible for the general structure of Saturnís ring system,
equation 3-1-20 for the case of a single SHP group (or .
To further narrow down the values of the dominant SHP group
responsible for the general structure of Saturnís ring system,
equation 3-1-20 for the case of a single SHP group (or
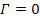 )
reduces to )
reduces to
Equation
5-3a 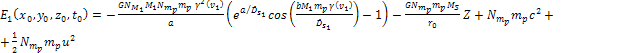
The
term
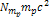 is independent of the locations of the minima, and thus bears
no influence on the morphology of the rings. Consequently, this term
may be dropped. As the ring particles reside above the surface of
Saturn, is independent of the locations of the minima, and thus bears
no influence on the morphology of the rings. Consequently, this term
may be dropped. As the ring particles reside above the surface of
Saturn,
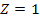 .
Furthermore, since the orbits of Saturnís rings and
satellites are in compliance with Keplerís laws of motion, the
following approximation can be made:14 .
Furthermore, since the orbits of Saturnís rings and
satellites are in compliance with Keplerís laws of motion, the
following approximation can be made:14 Equation
5-3b 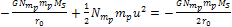
Therefore,
the maxima and minima of equation 5-3a are, for all practical
purposes, identical to the maxima and minima of Equation
5-3c 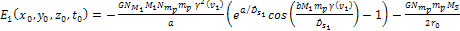
The
morphology
of planetary rings
is determined mainly by the locations of the potential energy minima,
rather than by the local magnitude of the potential energy level.
Although substantial (or even dominant), the contribution of
Saturnís
ordinary matter term 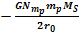 to the overall energy level of the object changes very gradually with
distance relative to the rate of change of the rapidly oscillating
contribution of the superheavy particles.
Therefore, the influence of Saturnís ordinary matter on the
local frequency and general shape of the potential energy
oscillations, as well as on the locations of the local minima, is
small. Consequently, the locations of the minima of
to the overall energy level of the object changes very gradually with
distance relative to the rate of change of the rapidly oscillating
contribution of the superheavy particles.
Therefore, the influence of Saturnís ordinary matter on the
local frequency and general shape of the potential energy
oscillations, as well as on the locations of the local minima, is
small. Consequently, the locations of the minima of 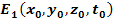 can be approximated by finding the locations of the minima of
can be approximated by finding the locations of the minima of Equation
5-3d 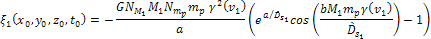
where
the contribution of Saturnís ordinary matter is absent.15
Equation 5-3d was employed to construct two dimensional color-coded
maps of the resultant calculated energies as functions of the SHP
mass
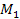 ,
the velocity of the SHP group ,
the velocity of the SHP group
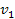 and its radius of orbit
and its radius of orbit
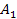 .16
The constructed maps were then compared with published images of
Saturnís main body of rings, which comprise of rings D, C, B, A
and the Cassini Division. .16
The constructed maps were then compared with published images of
Saturnís main body of rings, which comprise of rings D, C, B, A
and the Cassini Division.
Figure 5-1 provides a UG calculated map in comparison to an observed
image of Saturnís ring system generated using RSS 3-wavelength
occultation data recorded by NASAís Cassini satellite, which
samples a single trace radially through the rings. A reasonably good
fit was found using a single group of SHP mass
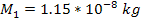 rotating at a speed of
rotating at a speed of
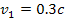 in a circular orbit of radius
in a circular orbit of radius
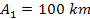 around the center of Saturn. The calculated map of Saturnís
ring plane, drawn between the planet and the edge of the A ring at
around the center of Saturn. The calculated map of Saturnís
ring plane, drawn between the planet and the edge of the A ring at
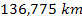 ,
reveals large spiral structures encircling the planet. A low level
of potential energy, and therefore a high density of matter, can be
observed in the lighter areas of the UG map (demonstrated in the
vicinity of ,
reveals large spiral structures encircling the planet. A low level
of potential energy, and therefore a high density of matter, can be
observed in the lighter areas of the UG map (demonstrated in the
vicinity of
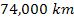 and
and
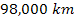 ),
and a high level of potential energy, and therefore a low density of
matter, or even gaps are observed in darker regions (viewed in the
vicinity of ),
and a high level of potential energy, and therefore a low density of
matter, or even gaps are observed in darker regions (viewed in the
vicinity of
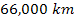 , ,
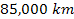 and
and
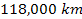 from the planetary center). At a display resolution of lower than
approximately
from the planetary center). At a display resolution of lower than
approximately
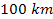 ,
the calculated map bears a significant resemblance to the observed
large-scale structure of Saturnís ring system. However, figure
5-1a, as well as other observed images recorded by Cassini and
Voyager, reveals additional fine structure that is not present in the
simple calculated model of a single SHP group. As discussed, in
order to provide for the general large-scale as well as the
fine-scale structure of Saturnís rings (while keeping the
complexity of the model to a minimum), a second orbiting SHP group of
the same SHP type was added. ,
the calculated map bears a significant resemblance to the observed
large-scale structure of Saturnís ring system. However, figure
5-1a, as well as other observed images recorded by Cassini and
Voyager, reveals additional fine structure that is not present in the
simple calculated model of a single SHP group. As discussed, in
order to provide for the general large-scale as well as the
fine-scale structure of Saturnís rings (while keeping the
complexity of the model to a minimum), a second orbiting SHP group of
the same SHP type was added.
Following equation 5-1, the velocity
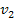 and the orbital radius
and the orbital radius
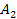 of the second group are related via
of the second group are related via
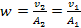 . The velocity
. The velocity
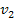 and the radius of orbit
and the radius of orbit
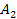 were calculated using the fine structure observed in the D ring.
were calculated using the fine structure observed in the D ring.
Closest to Saturn, the D ring consists of a number of faint, narrow
ringlets. The inner edge of the D ring is indistinct, and the forces
that sustain this part of the ring are poorly understood.
Furthermore, as shown in figure 5-2a, a new type of regular pattern,
yet unexplained, was detected in the gap between the D73 ringlet and
the C ring. This pattern was found to consist of a fine structure of
a wavelength of approximately
 (Hedman, Burns & Showalter, 2007). (Hedman, Burns & Showalter, 2007).
In order to calculate the parameters of the second SHP group,
equation 5-3d must be modified to include its contribution to the
potential energy of the object, leading to Equation
5-4 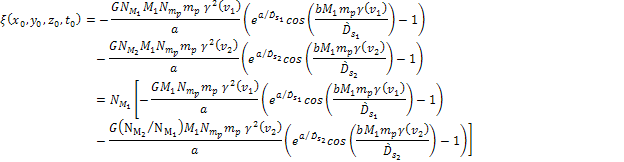
where
again, the exponent values can be replaced by
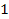 .
The same values of .
The same values of
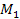 , ,
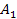 and
and
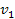 used in figure 5-1b were applied in conjunction with a new set of
independent parameters,
used in figure 5-1b were applied in conjunction with a new set of
independent parameters,
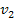 and
and
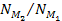 ,17
to calculate two dimensional maps based on equation 5-4. A
relatively good fit, which retained the large-scale pattern while
successfully producing the ,17
to calculate two dimensional maps based on equation 5-4. A
relatively good fit, which retained the large-scale pattern while
successfully producing the
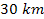 wavelength of the fine structure along the outer edge of the D ring
and into the C ring, was achieved with the addition of a group of
superheavy particles of the same particle mass
wavelength of the fine structure along the outer edge of the D ring
and into the C ring, was achieved with the addition of a group of
superheavy particles of the same particle mass
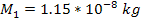 ,
rotating in a circular orbit around the center of Saturn at a
relativistic speed of about ,
rotating in a circular orbit around the center of Saturn at a
relativistic speed of about
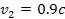 (the value of
(the value of
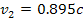 was used). The corresponding radius of the second group is therefore
equal to
was used). The corresponding radius of the second group is therefore
equal to
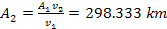 .
According to observations, Saturnís main body of rings
contains areas of abundant ultra-fine structure separated by areas
with little or no fine structure. This restricts the value of the
ratio .
According to observations, Saturnís main body of rings
contains areas of abundant ultra-fine structure separated by areas
with little or no fine structure. This restricts the value of the
ratio
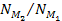 to the order of
to the order of
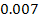 .
In the following discussion the value of .
In the following discussion the value of
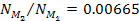 will be used.18
will be used.18
Although application of
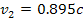 provided reasonable agreement with observations, the range of
possible velocities is not narrow, and in some of the following
images a higher value, somewhere in the range between
provided reasonable agreement with observations, the range of
possible velocities is not narrow, and in some of the following
images a higher value, somewhere in the range between
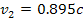 and
and
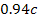 ,19
may provide better results. Figure 5-2 displays a calculated section
of Saturnís D ring, compared with a view of the fine structure
between the D73 ringlet and the C ring taken with the Cassini
Spacecraft narrow-angle camera. In figure 5-2b, the UG pattern
calculated with ,19
may provide better results. Figure 5-2 displays a calculated section
of Saturnís D ring, compared with a view of the fine structure
between the D73 ringlet and the C ring taken with the Cassini
Spacecraft narrow-angle camera. In figure 5-2b, the UG pattern
calculated with
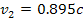 provides for the faint features of the D ring, as well as the inner
region of the C ring, visible at the upper left corner of the images.
The pattern further produces a regular pattern with a wavelength of
provides for the faint features of the D ring, as well as the inner
region of the C ring, visible at the upper left corner of the images.
The pattern further produces a regular pattern with a wavelength of
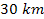 .
However, the calculated figure notably demonstrates fewer waves than
observed by Cassini in figure 5-2a. Increasing the velocity to .
However, the calculated figure notably demonstrates fewer waves than
observed by Cassini in figure 5-2a. Increasing the velocity to
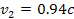 in figure 5-2c resulted in improved agreement, but reduced the
wavelength of the fine structure to a range of about
in figure 5-2c resulted in improved agreement, but reduced the
wavelength of the fine structure to a range of about
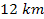 to
to
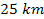 ,
which is less than the reported ,
which is less than the reported
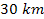 wavelength (Hedman, Burns & Showalter, 2007).
Therefore, the precise velocity is expected to fall somewhere between
wavelength (Hedman, Burns & Showalter, 2007).
Therefore, the precise velocity is expected to fall somewhere between
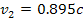 and
and
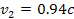 .20 .20

5-1b:
UG
calculated image of Saturnís
main rings.

Figures
5-1a and 5-1b:Displays a
comparison between the UG calculated zones providing rings D,C,B, A
and the Cassini Division
(figure 5-1b) and Saturnís
observed ring profile (figure 5-1a). In figure 5-1a areas depicted
in green and blue are dominated by small particles, and areas
indicated in violet consist mainly of large particles. White areas
indicate regions that were so opaque that the size of particle
could not be determined. Image
credit for figure 5-1a: NASA/JPL;
http://photojournal.jpl.nasa.gov/catalogue/PIA07872.

Figure
5-2a: Image
obtained from NASA/JPL/Space
Science Institute. http://photojournal.jpl.nasa.gov/catalog/?IDNumber=PIA08990.
Figure
5-2b:
Calculated using 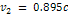

Figure
5-2c:
Calculated using 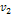 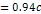
Figure 5-3 displays the calculated narrow radial section of the D
ring in the range of
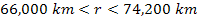 ,
providing a number of faint, narrow ringlets, in agreement with
observations. ,
providing a number of faint, narrow ringlets, in agreement with
observations. The C ring displays several empty
gaps containing sharp, eccentric ringlets.
While according to current theory, a few of the gaps may be
identified with satellite resonances, a number of observed gaps
remain unexplained. The ring pattern consists of spiral waves, as
well as bright regions of high particle density informally referred
to as ďplateaus.Ē The density of
particles is relatively uniform within the boundaries of the
plateaus, and their sharp structure is maintained despite the
expected spreading or diffusion of material. A view of the outer C
ring and the surrounding Maxwell gap is
displayed in figure 5-4, providing the
comparison between a calculated section (figure 5-4a) and an observed
view of the ring obtained by Cassini (figure
5-4b). Both images reveal a series of regularly
spaced plateau structures of about
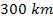 wide, nearly symmetrically placed around the Maxwell Gap. Note that
there is no known satellite or resonant structure to explain this
symmetrical placement.
wide, nearly symmetrically placed around the Maxwell Gap. Note that
there is no known satellite or resonant structure to explain this
symmetrical placement.
The B ring is dense, bright, massive and radially
extensive, demonstrating successive regions of abundant fine-scale
structure as well as irregular regions with little or no fine
structure occuring on a scale of
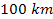 or more. There are no clear gaps in the ring,
however the Huygens gap, which contains an eccentric ringlet, resides
at its outer edge. Whereas the confining mechanism of the B ringís
inner boundary is unknown, its outer boundary is currently thought to
be caused by a 2:1 resonance with the satellite Mimas.
or more. There are no clear gaps in the ring,
however the Huygens gap, which contains an eccentric ringlet, resides
at its outer edge. Whereas the confining mechanism of the B ringís
inner boundary is unknown, its outer boundary is currently thought to
be caused by a 2:1 resonance with the satellite Mimas.
 
Figure
5-3:
Display of the
calculated structure of narrow ringlets
within the D ring using
the parameters 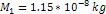 , ,
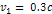 , ,
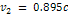 , ,
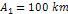 ,
and ,
and 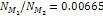 . .

Figure
5-4a:21
UG calculated
Figure
5-4b: Image credit:
NASA/JPL/Space Science
Institute; http://photojournal.jpl.nasa.gov/catalog/PIA06540.
Figure 5-5 displays a calculated section of the B ring (figure 5-5a)22
compared with an image shuttered by NASAís Cassini satellite of
the lit face of its middle region (figure 5-5b). Both figures
demonstrate abundant structure with a scale of a few hundred
kilometers and very little ultrafine-scale structure.
Very-fine-scale structure is observed in the outer B ring, shown in
figure 5-6c.

Figure
5-5a: UG calculated B
ring section.
Figure
5-5b: Image credit:
NASA/JPL/Space Science
Institute;
http://photojournal.jpl.nasa.gov/catalog/PIA06535.
Figure 5-6a provides the calculated two dimensional map of the outer
B ring, the Cassini Division and the lower A ring. Areas of abundant
ultra-fine structure can be noted within this region. Figures 5-6b
and c provide a comparison between the calculated region of the
Cassini division external to the bright outer B ring (figure 5-6b)23
and an observed image obtained by Cassini (figure 5-6c).
The calculated zonal structure provides the general regular pattern
observed in the rings of the Cassini division.

Figure 5-6a: A UG
calculated two dimensional map of the outer B ring, the Cassini
Division and the lower A ring.

Figure 5-6b:
UG Calculated B ring section.
Figure
5-6c:
Outer B ring, image credit: NASA/JPL/Space
Science Institute;
http://photojournal.jpl.nasa.gov/catalogue/PIAA06535.
Figure 5-7a displays a detail of Saturnís A ring interior to
the Encke gap taken by the Cassini ISS instrument. On the right the
image reveals spiral bending waves, where the wavelength decreases
inwards, and on the left a succession of spiral density waves, where
the wavelength decreases outwards. As the image is viewed from the
unlit side of the rings, opaque regions appear darker. In the
calculated UG model similar patterns of spiral density and bending
waves were found in several rings. A section of spiral waves in the A
ring is demonstrated in figures 5-7b, 5-7c and 5-7d. Note that in
figure 5-7b, drawn with
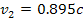 ,
the calculation provides fewer waves than observed. Elevating the
velocity of the second SHP group to ,
the calculation provides fewer waves than observed. Elevating the
velocity of the second SHP group to
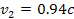 increases the number of waves, and in the case of the D ring, results
in better agreement with observation, as displayed in low resolution
in figure 5-7c and in higher resolution in figure 5-7d. In addition,
both the calculated and observed images of figure 5-7 reveal regions
of abundant fine-scale structure adjacent to smooth regions of little
or no fine-scale structure. Note that figure 5-7c, where the velocity
of the second of SHP group
increases the number of waves, and in the case of the D ring, results
in better agreement with observation, as displayed in low resolution
in figure 5-7c and in higher resolution in figure 5-7d. In addition,
both the calculated and observed images of figure 5-7 reveal regions
of abundant fine-scale structure adjacent to smooth regions of little
or no fine-scale structure. Note that figure 5-7c, where the velocity
of the second of SHP group
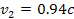 ,bears a particularly close resemblance to the observed
A ring. ,bears a particularly close resemblance to the observed
A ring.
The spiral that produces the F ring is likely to be a continuation of
the spiral which forms the D,C, B, and A rings and the Cassini
division. Following the discussion in footnote 91 of this chapter,
the Roche midsection, where rings and satellites coexist, starts at
about the radius of the satellite Pan. The gaps observed between the
A ring and the F ring and beyond the F ring may be located at the UG
sub-zones where the cosine terms either enhance coalescence, or are
too small to prevent the ring particles from coalescing into
satellites. These gaps may also be cleared by the gravitational
effect of nearby satellites, such as Atlas, Prometheus, Pandora or
Mimas, via resonances or the mechanism summarized in section V-1.
Therefore, the F ring is likely to be a narrow ring that is contained
within a zone in which matter cannot coalesce, surrounded from both
sides by areas where matter is swept away. Recall that the value of
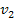 between
between
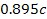 and
and
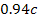 was derived from the observed wavelength of the ringlets in the D
ring, and seems to be confirmed by the agreement between the
calculated and the observed ring sections provided in figures 5-1 to
5-7. This range of velocity provides for fine structure in the range
of
was derived from the observed wavelength of the ringlets in the D
ring, and seems to be confirmed by the agreement between the
calculated and the observed ring sections provided in figures 5-1 to
5-7. This range of velocity provides for fine structure in the range
of
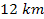 to
to
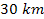 in wavelength. However, Saturnís rings appear to contain some
ultra-fine structure in the range of few kilometers or less.
Consequently, for stronger agreement between theory and observation,
three or more SHP groups may be required.
in wavelength. However, Saturnís rings appear to contain some
ultra-fine structure in the range of few kilometers or less.
Consequently, for stronger agreement between theory and observation,
three or more SHP groups may be required.
There is still the question of what provides for the stability of
these wide rings. In the Newtonian scenario, during each orbital
rotation a ring object must lose a minute amount of energy in the
form of gravitational radiation. As the objectís energy is
reduced continuously, its orbit is expected to draw closer and closer
to the planet, until eventually becoming consumed by it. This
process may last for at most few tens of millions of years before the
ring system dissipates completely. Within this timeline, Saturnís
rings would be expected to have existed for 100 million years at
most, a period which is too short to allow for the presence of the
elaborate fine structure observed. For Saturnís ring system to
remain stable over the length of time required for the formation of
its fine structure, there must be a continuous source of new energy
or new matter to replenish the ring system.
The answer to this question is much simpler in the case of
non-relativistic SHP velocities, as is probably the case with
Uranus, where a majority of the potential energy minima (and
therefore a majority of the rings) are very narrow. In cases of
non-relativistic SHP groups, the minima within the ring plane are
arranged in sets of stationary concentric circular contours. To
escape from any of these stationary minima, the energy of the ring
particle must be elevated; thus, the most stable state of the matter
within the ring is to remain at its given minimum. However, the
situation is slightly more complicated in the case of relativistic
SHP groups, as in the case of Saturn, where the density waves
produced by the SHP groups rotate at a much faster rate than the ring
matter. Hence, the minima locations are not stationary, and the
orbiting object moves too slowly to keep pace with its minimum.
Therefore, the object crosses paths with both the
local minimum and the local maximum on a periodic basis.24
In this case, the rotating zonal pattern driven by the rotating SHP
groups can provide a mechanism to replenish any energy losses due to
radiation, or attributed to other bodies interacting with the ring
matter. As previously discussed, due to the finite propagation speed
of gravitation, the relativistic rotation of SHP groups around the
planetary center generates rapidly rotating potential energy spiral
structures. Consequently, an orbiting ring particle in the path of
the rapidly rotating spiral structure encounters an endless series of
rapid oscillations that, along with their maxima and minima,
propagate outward at relativistic speeds.25

Figure
5-7a: Spiral bending
waves (right) and density waves in
Saturnís A ring
interior to the Encke Gap.
Image credit:
NASA/JPL/Space Science
Institute; http://photojournal.jpl.nasa.gov/catalogue/PIA06093.
Figure
5-7b:
Calculated using 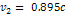 . .

Figure
5-7c: Calculated
using 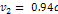 . .
Figure 5-7d:Calculated
at higher resolution using 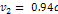 . .
As
the observed orbital period of the ring matter is Keplerian, the
overall force exerted on the ring particles is very close to
Newtonís gravitational force (see section V-6), and
consequently, the particles cannot be accelerated to the high
velocities needed to keep up with the high propagation speed of the
minima of the rotating pattern of the potential energy. Therefore,
the rapid, outward moving maxima and minima contours will encounter
the orbiting object on a periodic basis, where the time between two
successive respective encounters is less than or approximately equal
to
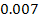 seconds, the approximate time it takes the SHP groups to complete one
full rotation.26
As the object must encounter an oscillation maximum every
seconds, the approximate time it takes the SHP groups to complete one
full rotation.26
As the object must encounter an oscillation maximum every
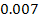 seconds or less, the minute amount of energy lost during one orbital
period will be replenished by the next encounter with the following
maximum. These periodic encounters create a barrier that prevents
the object from gradually losing energy and falling towards the
planet. Hence, the orbiting object behaves as a driven harmonic
oscillator, where the force applied on the object by the rotating
spiral pattern of the SHP groups provides a periodic driving force.
As the overall motion of the object is in accordance with Keplerís
laws, this driving force is substantially smaller, yet not negligible
relative to the force applied by Saturnís ordinary matter.
Thus, the force exerted by the orbiting SHP groups provides a small
perturbation to the overall force exerted by the planetary ordinary
matter, causing the rotating object to oscillate slightly around its
Keplerian orbit.
seconds or less, the minute amount of energy lost during one orbital
period will be replenished by the next encounter with the following
maximum. These periodic encounters create a barrier that prevents
the object from gradually losing energy and falling towards the
planet. Hence, the orbiting object behaves as a driven harmonic
oscillator, where the force applied on the object by the rotating
spiral pattern of the SHP groups provides a periodic driving force.
As the overall motion of the object is in accordance with Keplerís
laws, this driving force is substantially smaller, yet not negligible
relative to the force applied by Saturnís ordinary matter.
Thus, the force exerted by the orbiting SHP groups provides a small
perturbation to the overall force exerted by the planetary ordinary
matter, causing the rotating object to oscillate slightly around its
Keplerian orbit.
Consequently, the force generated by the rapidly rotating SHP groups
is demonstrated to provide a mechanism by which the energy lost by
orbiting material is replenished to maintain the ring structure over
time, thus allowing for the long-term stability of planetary ring
systems. The oscillating waves created by the rotating spiral are
calculated to propagate outwards at relativistic speeds, and are
certainly not stationary. Conversely, images of Saturnís rings
reveal relatively little fluctuation in the orbital locations of
certain rings or gaps over time. The rapid movement of the calculated
oscillating patterns, however, does not contradict observations of
stable ring orbits and gaps, since our perception of the ring
characteristics at a given location is driven by the amplitude and
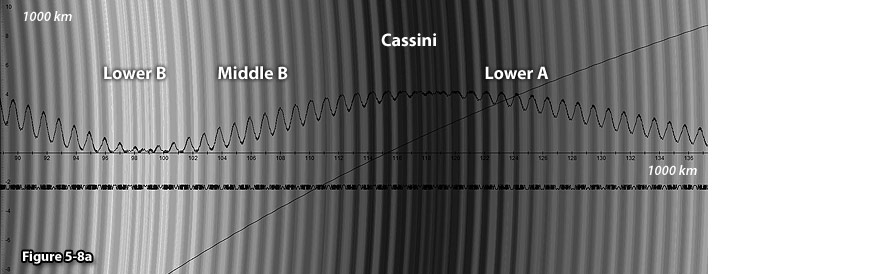
frequency of the oscillating waves, rather than by their phase.27 In figure 5-8 three waveforms are
overlayed with two dimensional calculated images of the potential
energy of the given object.28
The oscillating waveform displayed entirely above the
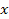 axis provides the total contribution of both SHP
groups, without the contribution of Saturnís
ordinary matter. The second waveform, characterized by distinct
trains of rapid oscillations, is displayed entirely below the
axis provides the total contribution of both SHP
groups, without the contribution of Saturnís
ordinary matter. The second waveform, characterized by distinct
trains of rapid oscillations, is displayed entirely below the
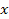 axis and provides the exclusive contribution of the second SHP
group (with
axis and provides the exclusive contribution of the second SHP
group (with
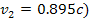 .
The third smooth waveform crossing the .
The third smooth waveform crossing the
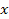 axis provides the overall contribution of Saturnís ordinary
matter and the significantly smaller contribution of both SHP
groups (given by the first waveforms).29
As demonstrated in the figure, the potential energy of the SHP
contribution is highest within the area covered by the Cassini
Division (between approximately
axis provides the overall contribution of Saturnís ordinary
matter and the significantly smaller contribution of both SHP
groups (given by the first waveforms).29
As demonstrated in the figure, the potential energy of the SHP
contribution is highest within the area covered by the Cassini
Division (between approximately
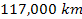 and
and
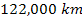 )
where the oscillations of the upper waveform appear to almost
flatten, with significant reduction in amplitude and wavelength. This
process further accounts for low particle density in the Cassini
Division. The Cassini Division is located in the vicinity of a zonal
maximum of the first SHP group with a velocity of )
where the oscillations of the upper waveform appear to almost
flatten, with significant reduction in amplitude and wavelength. This
process further accounts for low particle density in the Cassini
Division. The Cassini Division is located in the vicinity of a zonal
maximum of the first SHP group with a velocity of
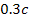 (see figures 5-8a and b), where the amplitude of the local
oscillations nearly diminishes. In areas where the oscillation
amplitude diminishes completely, the periodic driving force will
reduce to zero, and the ring material will dissipate over time to
produce a gap. In the remaining areas of the Cassini Division, where
the oscillation amplitude is significantly reduced but not entirely
eliminated, a very faint ring structure may be observed. Based
on the above discussion, strong rings should be observed in regions
where the amplitude of the outward moving oscillations is
substantial. Looking at the same image, the relatively large
amplitude of the oscillations produced by the upper waveform between
(see figures 5-8a and b), where the amplitude of the local
oscillations nearly diminishes. In areas where the oscillation
amplitude diminishes completely, the periodic driving force will
reduce to zero, and the ring material will dissipate over time to
produce a gap. In the remaining areas of the Cassini Division, where
the oscillation amplitude is significantly reduced but not entirely
eliminated, a very faint ring structure may be observed. Based
on the above discussion, strong rings should be observed in regions
where the amplitude of the outward moving oscillations is
substantial. Looking at the same image, the relatively large
amplitude of the oscillations produced by the upper waveform between
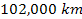 and the Cassini division (starting at about
and the Cassini division (starting at about
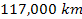 )
explains the absence of gaps, as well as the
relatively large optical depth of the B ring. An abundance of fine
structure in the outer B ring can also be noted. As demonstrated in
the figure, the oscillation amplitude of the contribution of the
first SHP group in the middle B ring is
significantly larger than the oscillation amplitude contributed by
the second SHP group, however both contributions
become comparable in size at the distance range of the upper B ring
and the Cassini Division. Therefore, the fine structure oscillations
contributed by the second group in the middle section of the B ring
are insignificant (see Figure 5-8a), while in the general area of the
Cassini Division the fine structure becomes relatively substantial.
An enlarged view of the Cassini Division surrounded by the outer B
ring and the inner A ring is provided in figure
5-8b. As expected, the ring structure in this area displays an
abundance of fine structure. )
explains the absence of gaps, as well as the
relatively large optical depth of the B ring. An abundance of fine
structure in the outer B ring can also be noted. As demonstrated in
the figure, the oscillation amplitude of the contribution of the
first SHP group in the middle B ring is
significantly larger than the oscillation amplitude contributed by
the second SHP group, however both contributions
become comparable in size at the distance range of the upper B ring
and the Cassini Division. Therefore, the fine structure oscillations
contributed by the second group in the middle section of the B ring
are insignificant (see Figure 5-8a), while in the general area of the
Cassini Division the fine structure becomes relatively substantial.
An enlarged view of the Cassini Division surrounded by the outer B
ring and the inner A ring is provided in figure
5-8b. As expected, the ring structure in this area displays an
abundance of fine structure.
Figure
5-8a:
UG calculated ring section.
Viewing
the fine structure presented by the upper curve in figure 5-8b, the
wavelengths of any two adjacent sections of rapidly oscillating waves
are shown to increase in opposite directions. This may explain the
observed occurrence of spiral density waves,
where the wavelength decreases outward, as well as spiral bending
waves, where the wavelength decreases inwards
(See figure 5-7). Note that according to current theory, spiral
density or bending waves are thought to be created by gravitational
interactions with Saturnís moons.
However, in many instances, no sufficiently large moons were found
in proper locations for creating them.
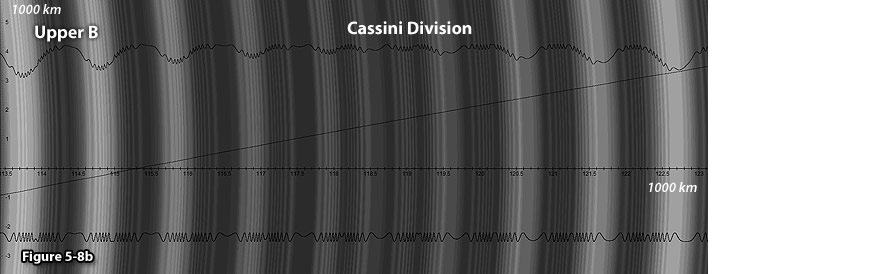
Figure 5-8b:
UG calculated ring section.
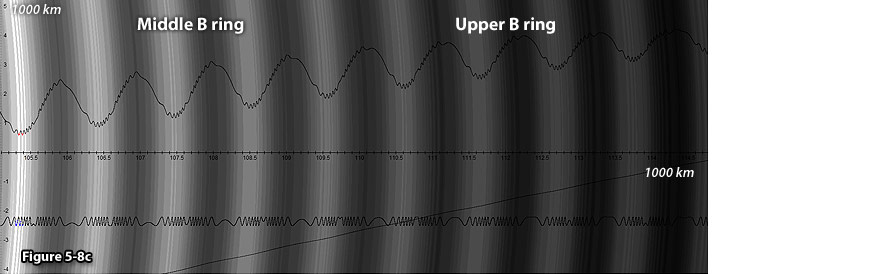
Figure 5-8c displays an enlarged view of the middle B
ring. The calculated waveforms overlayed on the two dimensional
image demonstrate long stretches of over one hundred kilometers of
little or no fine structure. In figure 5-8d, the calculated display
is extended to cover Saturnís D, C, B and
A rings and the Cassini division. Note the
similarities between the oscillation patterns extending from about
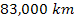 to
to
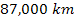 ,
and between those extending from about ,
and between those extending from about
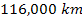 to
to
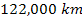 .
This may account for the structural similarities observed between the
C ring and the Cassini Division. .
This may account for the structural similarities observed between the
C ring and the Cassini Division.
Figure
5-8c: UG
calculated ring section.
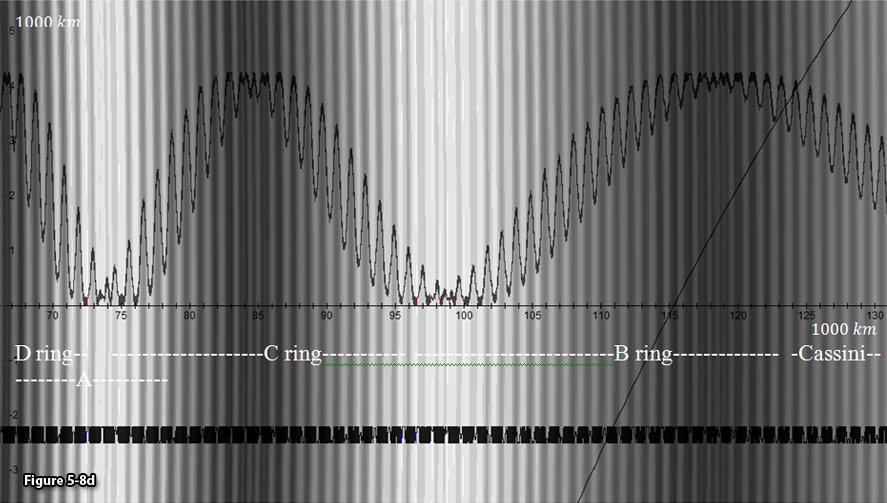
Figure
5-8d:
UG calculated ring section.
Section V-3: The
Phenomenon of Spokes
One
of the more peculiar phenomena observed in Saturnís rings are
the spokes, first observed by Voyager in 1980. Spokes are nearly
radial structures, observed to appear intermittently in the B ring.
Viewed from low phase angles (shown in figure 5-9c), they appear as
dark markings along a bright underlying B ring. Conversely, spokes
may appear brighter than the ring when viewed at high phase angles,
or against the ringís unilluminated side (see figure 5-9d). A
surprising property of the spokes is that they maintain their shape
in spite of the differential rotation that occurs in the underlying B
ring. This indifference to rotation is not consistent with orbital
mechanics, and cannot be explained by Newtonian gravitational forces.
As they are observed to rotate at approximately the same rate as the
rotation of Saturnís magnetic field, spokes are commonly
attributed to interactions of charged particles with Saturnís
magnetic field, however the origin and exact nature of these features
are not yet well understood.
According to the UG theory, the phenomenon of spokes can be explained
as a by-product of a relativistic effect, where a pattern is
generated as a consequence of the relativistic distortion of
spacetime by the rotating SHP groups, and captured by the cameraís
matrix of sensors. This calculated phenomenon is demonstrated in
figure 5-9a, where equation 5-3d was used in order to show that even
a single SHP group is capable of creating spoke structures. The
equation was applied using the parameters of the first SHP group (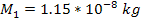 , ,
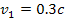 , ,
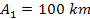 ,
and for simplicity, ,
and for simplicity,
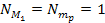 ).
The resultant figure displays a two dimensional image of the
rotation plane of Saturnís rings, drawn using a single
threshold level ).
The resultant figure displays a two dimensional image of the
rotation plane of Saturnís rings, drawn using a single
threshold level
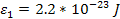 in order to maintain a high level of contrast. Consequently, any
position on the ring plane where
in order to maintain a high level of contrast. Consequently, any
position on the ring plane where
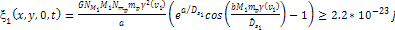 was layered in gray, while any position where
was layered in gray, while any position where
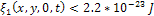 was indicated in white. The resultant set of rings
display features that fit the general description of spokes as
observed in figures 5-9c and 5-9d.30
Moreover, the locations of the calculated spokes remain stationary
over time relative to the frame of reference of the planetary center,
which implies that they rotate with Saturn while maintaining their
shape, as observed. It is further implied that these features are
fixed within the coordinate axes. As the rotation rate of Saturnís
magnetic field is very close to the overall rotation rate of the
planet around its axis, the calculated spokes appear to rotate at
approximately the same rate as Saturnís magnetic field. was indicated in white. The resultant set of rings
display features that fit the general description of spokes as
observed in figures 5-9c and 5-9d.30
Moreover, the locations of the calculated spokes remain stationary
over time relative to the frame of reference of the planetary center,
which implies that they rotate with Saturn while maintaining their
shape, as observed. It is further implied that these features are
fixed within the coordinate axes. As the rotation rate of Saturnís
magnetic field is very close to the overall rotation rate of the
planet around its axis, the calculated spokes appear to rotate at
approximately the same rate as Saturnís magnetic field.

Figure
5-9a: Displays spoke
features in the rings. The calculated figure was generated using
parameters of 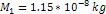 , ,
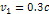 , ,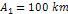 and
and 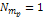 ,where the point ,where the point 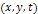 is layered only if
is layered only if 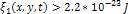 and
and 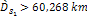 . .
The visibility of spokes and the clarity of their patterns may
depend on the angle between the Sun and the rotation plane of the
rings, or on the angle between the camera and the ringsí
rotation plane.31
This may account for the intermittent appearance of spokes in the B
ring, which is currently attributed to their being a seasonal effect.
In addition, although spokes are uniquely observed in the dense and
massive B ring, the calculated figure shows that spoke features can
appear in other rings as well, suggesting that the visibility of the
radial spokes may further depend on the density of ring matter or on
the size of the ring particles.
Figure
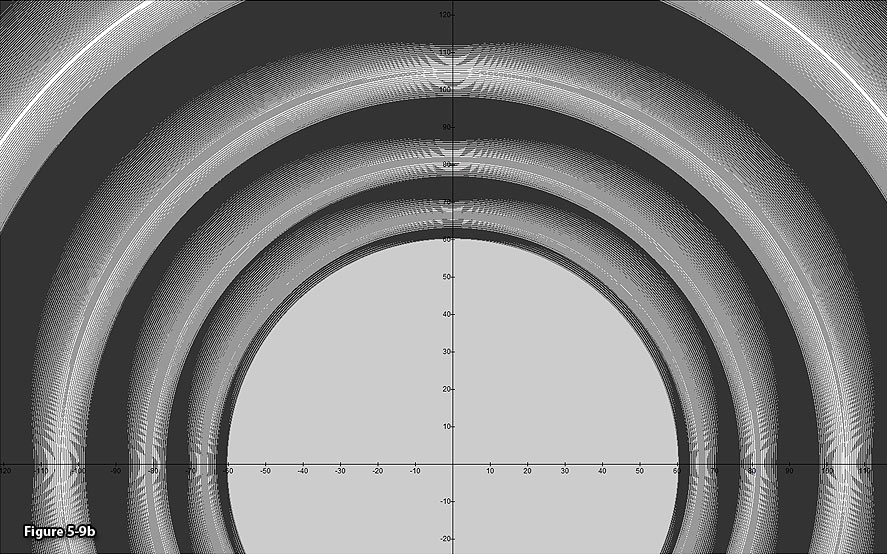
5-9b: In order to
provide a vivid image of spoke features, the parameters were modified
to 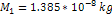 , ,
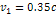 and
and 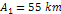 ,
where the point ,
where the point 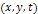 is layered only if
is layered only if 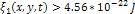 and
and 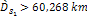 . .

Figures 5-9c and
5-9d: Voyager
images of radial spokes in Saturnís
B ring. Spokes appear
dark against the B ring at low phase angles (5-9c) and bright against
the B ring at high phase angles (5-9d). Credit
for figure 5-9c: image obtained by Voyager
2; NASA/JPL;
http://photojournal.jpl.nasa.gov/catalogue/PIA02275. Credit
for image 5-9d: image obtained by Voyager
1; NASA/JPL;
http://photojournal.jpl.nasa.gov/catalogue/PIA02269.
Section V-4: The
Non-Circular Shape of the B Ring
Due
to the effects of special relativity, superheavy particles rotating
at relativistic velocities create a distortion of spacetime. As a
result of this distortion, and of the finite speed of gravitation,
the otherwise circular zonal minima are replaced by a distorted
rotating spiral. Hence, the width of the ring will vary with
azimuth, and its orbit will depart from a pure circular shape. This
effect becomes stronger as the orbital speeds of the SHP groups
increase and their radii of orbit are reduced. As demonstrated in
figures 5-9a and 5-9b, the calculated zonal structure and its minima
expand outwards, where the level of expansion varies with the azimuth
of the ring section, resulting in a non-circular outer boundary of
the rings, while the inner boundary retains a circular morphology.
The non-circular structure of the outer edge of the rings resembles
the boxiness observed in galaxies (see Chapter VII), as both
phenomena are created by the same relativistic effect. Similar to
the dynamics of the calculated radial spokes in Saturnís B
ring, the calculated ring boundaries maintain their shape in spite of
the differential rotation that occurs in the underlying B ring. In
figures 5-9a and b, all of the calculated rings demonstrate some
degree of boxiness.
Section
V-5: The Dynamics of Ring Variability Over Time and Azimuth
Data obtained by Voyager and Cassini reveals that ring structure
varies with time and azimuth. Figure 5-10a provides a composite
image of four views of the outer edge of the B ring, assembled from
images shuttered by Voyager 2 at two different times and at two
different azimuths (Miner, Wessen & Cuzzi, 2007).
An offset of about
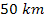 in the radius of the outer edge of the B ring as well as significant
mismatch in its fine structure can be noted.32
These findings can be explained by two different phenomena.
Boxiness, explained above, may account for a large part of the
in the radius of the outer edge of the B ring as well as significant
mismatch in its fine structure can be noted.32
These findings can be explained by two different phenomena.
Boxiness, explained above, may account for a large part of the
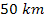 offset of the outer edge of ring B between the two azimuths. In
addition, as the zonal structure is driven by a rapidly rotating
spiral that changes over time and azimuth, the ring pattern is also
expected to shift over time and to change between different azimuths.
Both SHP groups are calculated to complete a full rotation in about
offset of the outer edge of ring B between the two azimuths. In
addition, as the zonal structure is driven by a rapidly rotating
spiral that changes over time and azimuth, the ring pattern is also
expected to shift over time and to change between different azimuths.
Both SHP groups are calculated to complete a full rotation in about
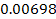 seconds, suggesting that some features of the fine structure of the
rings must change at a rapid rate.
seconds, suggesting that some features of the fine structure of the
rings must change at a rapid rate.
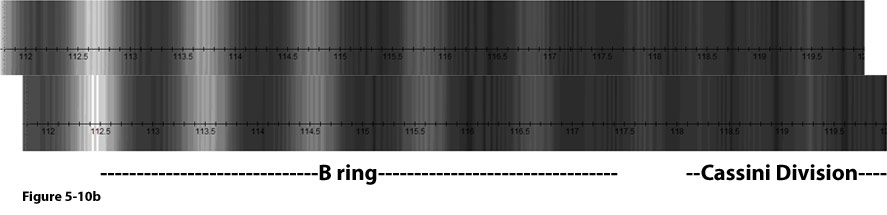
Figure 5-10b displays two calculated radial sections of the same
region covering the outer edge of the B ring and the inner Cassini
Division at two different times
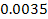 seconds apart. The images are positioned so that their large-scale
pattern is aligned. Note that similar to observations, the fine
structure in the outer B ring does not match between the calculated
images. Mismatch is also observed, but to a lesser degree, in the
Cassini Division.
seconds apart. The images are positioned so that their large-scale
pattern is aligned. Note that similar to observations, the fine
structure in the outer B ring does not match between the calculated
images. Mismatch is also observed, but to a lesser degree, in the
Cassini Division.

Figure
5-10a: The composite
image of four views of the outer edge of the B ring assembled from
images collected by the Voyager
2 Spacecraft. Displayed on the left is the bright B ring, at the
center is the dark Huygens gap (of variable width) containing a
narrow elliptical ringlet, and on the right is the Cassini
Division (Voyager 2 image
260-1473, obtained from Miner, Wessen & Cuzzi, 2007).
Section
V-6:
Estimating the Overall Mass and Abundance of Superheavy Particles
of Mass 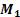 Thus
far, the following parameters of the two SHP groups were estimated:
the SHP mass
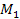 ,
the orbital radii ,
the orbital radii
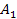 and
and
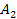 ,
the velocities ,
the velocities
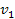 and
and
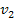 ,
and the approximate ratio of ,
and the approximate ratio of
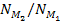 ,
where ,
where
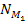 and
and
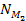 respectively denote the number of superheavy particles in the first
and second SHP groups. In addition, the mass of the Saturnís
ordinary matter
respectively denote the number of superheavy particles in the first
and second SHP groups. In addition, the mass of the Saturnís
ordinary matter
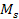 is already known. Still missing, however, is an assessment of the
approximate values of
is already known. Still missing, however, is an assessment of the
approximate values of
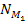 and
and
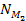 .33
Using Keplerís third law, the calculated orbital periods of
each of the known satellites internal to the orbit of Lapetus (at
about .33
Using Keplerís third law, the calculated orbital periods of
each of the known satellites internal to the orbit of Lapetus (at
about
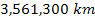 )34
were compared with their observed values. The calculated orbits were
found to fall between )34
were compared with their observed values. The calculated orbits were
found to fall between
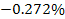 and
and
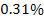 of the measured values (see table 5-1). As the effect exerted by
Saturnís superheavy particles is expected to cause the orbital
periods of the satellites to deviate from their Keplerian predicted
orbital periods, the measured deviations limit the possible number of
SHPs of mass
of the measured values (see table 5-1). As the effect exerted by
Saturnís superheavy particles is expected to cause the orbital
periods of the satellites to deviate from their Keplerian predicted
orbital periods, the measured deviations limit the possible number of
SHPs of mass
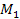 . .
Assuming a circular orbit of radius
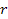 ,
the speed of a satellite ,
the speed of a satellite
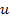 is related to its orbital period
is related to its orbital period
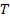 via the equation
via the equation
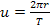 .
Therefore, as the deviation of the satelliteís orbital period
from its predicted value, denoted .
Therefore, as the deviation of the satelliteís orbital period
from its predicted value, denoted
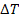 ,
is small relative to ,
is small relative to
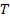 ,
the deviation of the square of the speed ,
the deviation of the square of the speed
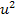 from the square of its Keplerian speed
from the square of its Keplerian speed
 (where
(where
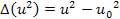 )
can be expressed as )
can be expressed as Equation
5-5 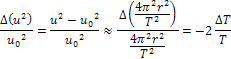
Keplerís
law is fulfilled if and only if
Equation
5-6
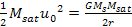 ,
or ,
or
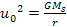
where
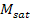 provides the mass of any one of the Saturian satellites and
provides the mass of any one of the Saturian satellites and
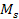 is the total mass of Saturn. Therefore, the deviation from Keplerís
predicted orbital period is given by
is the total mass of Saturn. Therefore, the deviation from Keplerís
predicted orbital period is given by Equation
5-7
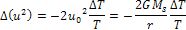
However,
the centrifugal force applied to the satellite is given by
Equation
5-8
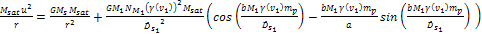
where
the exponent term was replaced by
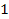 ,
as ,
as
 .
Also note that the contribution of the second SHP group to the
centrifugal force was dropped since .
Also note that the contribution of the second SHP group to the
centrifugal force was dropped since
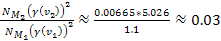 .3536
Consequently, the overall influence of the second SHP group on the
calculated velocity of the object is small relative to the influence
of the first group, and can thereby be neglected. Since .3536
Consequently, the overall influence of the second SHP group on the
calculated velocity of the object is small relative to the influence
of the first group, and can thereby be neglected. Since
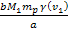 is of the order of
is of the order of
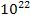 ,
the cosine term is negligible and can be omitted. Thus, ,
the cosine term is negligible and can be omitted. Thus, Equation
5-9
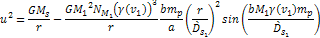
Combining equations
5-6, 5-7 and 5-8, under the assumption that the entire deviation is
due to the SHP effect, yields 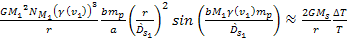
or Equation
5-10
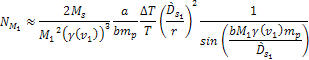
According
to table 5-1, the maximum deviation of an orbital period of a
satellite is within
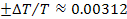 (see the satellite Anthe at
(see the satellite Anthe at
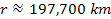 ).
Substituting ).
Substituting
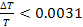 , ,
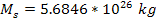 , ,
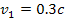 (therefore,
(therefore,
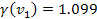 ),
and using the approximation of ),
and using the approximation of
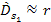 ,
equation 5-10 yields ,
equation 5-10 yields
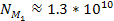 .
The earlier estimate of .
The earlier estimate of
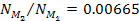 thus provides
thus provides
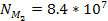 ,
which translates to a total of ,
which translates to a total of
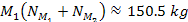 of SHPs of mass
of SHPs of mass
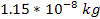 . .
Hence, the overall SHP mass is negligible compared with the overall
mass of Saturnís ordinary matter, and bears no influence on
objects dominated by the ordinary matter external to the zonal
oscillation range of the SHPs with ordinary matter.
Note, however, that the current published mass of Saturn was
calculated from the orbital periods of its satellites, under the
assumption that their motions are governed purely by Newtonian
dynamics. If the SHP contribution is taken into account, the mass of
Saturn may be altered by less than 0.3% (according to table 5-1), or
by an amount of the order of
 . .
Table
5-1: A comparison between the Keplerian calculated and the measured
orbital periods of Saturnís Satellites (the calculation uses
Keplerís third law, while arbitrarily assuming a perfect match
for Mimas). Satellite | semimajor axis | calculated
orbital period | measured
orbital period | |
| (*1000  ) ) | (Days) | (Days) | % change | | | | | | Mimas | 185.52 | 0.9424218 | 0.9424218 | 0 | Enceladus | 238.02 | 1.369554744 | 1.370218 | 0.048405179 | Tethys | 294.66 | 1.886431314 | 1.887802 | 0.072607505
| Dione | 377.4 | 2.734400117 | 2.736915 | 0.091887519 | Rhea | 527.04 | 4.512576593 | 4.5175 | 0.108985203 | Titan | 1221.83 | 15.92851895 | 15.945421 | 0.105999375 | Hyperion | 1481.1 | 21.25865545 | 21.276609 | 0.08438165 | Iapetus | 3561.3 | 79.26328361 | 79.330183 | 0.08433031 | Pan | 133.583 | 0.575819024 | 0.575 | -0.142438957 | Daphnis | 136.50 | 0.594782521 | 0.594 | -0.131737519 | Atlas | 137.67 | 0.602446088 | 0.6019 | -0.090727402 | Prometheus | 139.353 | 0.613527034 | 0.613 | -0.085976242 | Pandora | 141.70 | 0.629091758 | 0.6285 | -0.094154062 | Epimetheus | 151.422 | 0.694932603 | 0.6942 | -0.105531999 | Janus | 151.472 | 0.695276835 | 0.6945 | -0.111855264 | Methone | 194 | 1.007770903 | 1.01 | 0.220702653 | Anthe | 197.70 | 1.036738494 | 1.04 | 0.313606348 | Pallene | 211 | 1.143096521 | 1.14 | -0.271624679 | Calypso | 294.66 | 1.886431314 | 1.8878 | 0.072501638 | Telesto | 294.66 | 1.886431314 | 1.8878 | 0.072501638 | Helene | 377.40 | 2.734400117 | 2.7369 | 0.091339958 | Polydeuces | 377.40 | 2.734400117 | 2.74 | 0.204375303 |
Section V-7: Summary
A very simple model providing the interaction between two orbiting
SHP groups composed of a single superheavy particle type and a
spherically symmetric distribution of ordinary matter around the
center of Saturn produces a zonal pattern that bears a close
resemblance to the observed structure of Saturnís main body of
rings, and can further account for a number of ring characteristics,
including the appearance of spokes, gaps, ringlets, the appearance of
spiral density and bending waves, and the general fine structure
distribution. Note that the goal at this stage is limited to
demonstrating the power of the UG theory and its ability to provide
the general morphology and characteristics of complex systems on all
distance scales via the use of the simplest model possible. No
effort was made here to explain the remaining outer rings, such as
the G and E rings, or to extend the discussion to model the formation
and orbital locations of the Saturnian satellites. Saturnís
main rings were selected for a UG analysis as they are the most
complicated and the least understood rings observed to date. The same
tools used for the analysis of the Saturnian system can be used for
modeling the simpler rings and satellite systems of Jupiter, Uranus
and Neptune.
The success achieved by this simple model in explaining the complex
structure of Saturnís D, C, B, and A rings and the Cassini
Division, coupled with the success of an even simpler model (using a
single or binary SHP groups with as little as four parameters) in
explaining various morphologies observed in galaxies and nebulae (in
Chapter IV) provides a strong testament to the power of the UG
theory, and further suggests that the addition of few more SHP
groups, and additional fine-tuning of their parameters, may explain
these complex systems down to very fine details. The UG approach
suggests that the rings are generated by orbiting SHP groups, and
provides a mechanism to keep them stable over a long period of time.
As superheavy particles are most likely to be created by the collapse
of the cloud of gas that formed the planet (see Chapter VII),
planetary rings may be as old as their parent planets, and almost as
old as the Solar System itself. This resolves the current
contradiction, where according to the Newtonian scenario, the
observed planetary rings could not have existed for more than a few
tens of millions of years, while the Saturnian rings require a
significantly longer period of time for developing their complex fine
structure.
1A summary of what is known about
the planetary ring systems,
the current leading theories, and which features within the rings
have not yet been adequately explained is provided in Planetary
Ring Systems
by Miner et. al (Miner,
Wessen and
Cuzzi, 2007). 2
Another mechanism, known as a Lorentz resonance,
is theorized to be capable of creating planetary rings
with dust-size particles, by which small particles located slightly
inward to or outward from the Lorentz resonance radius experience
small forces that push them away from the resonance radius. Over
time, the region around the ring may become depleted of dust-size
particles. This process, however, cannot explain the existence of
rings consisting of larger objects. 3
Saturnís F ring
and the dense, narrow rings of Uranus
rings were initially thought to have formed via gravitational
shepherding. However, new discoveries have challenged this theory. 4
With the current available observation resolution, any satellites
with a diameter larger than one kilometer should have already been
detected. 5
An alternative theory suggests that the Uranian rings were formed by
the trapping of outward drifting particles between resonances of the
planetís inner satellites(Fridman &
Gorkavyi, 1994).
After their formation, the rings left the resonances that produced
them and drifted hundreds of kilometers toward their current
positions. 6It is current belief that
eruptions from the moon Enceladus
are the main source of material replenishment for Saturnís
E ring. 7NASA
(December 12, 2007). ďSaturnís
Rings May be Old Timers.Ē Press release.
Retrieved 2007-12-27. Archive
copy at
the Internet
Archive http://www.nasa.gov/mission_pages/cassini/media/cassini20071212.html. 8
The zonal oscillation range
of a superheavy particle of mass 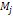 and an ordinary particle of mass
and an ordinary particle of mass 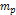 is given by
is given by 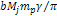 .
The planetary center is within the oscillation range
of the SHP, which orbits
at a radius .
The planetary center is within the oscillation range
of the SHP, which orbits
at a radius 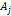 when
when 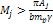 . . 9
In contrast, a superheavy particle group in orbit around the central
core moving at a speed of
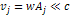 creates a narrow circular ring of the type demonstrated by Uranus.
creates a narrow circular ring of the type demonstrated by Uranus. 10
Planetary ring particles or objects are assumed to be too small to
support superheavy particles
of their own, thus they contain only ordinary matter. 11
Based on Newtonian gravitation,
a planetís Roche limit
resides at about 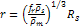 ,
where ,
where 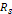 is the radius of the planet,
is the radius of the planet, 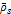 and
and 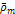 provide the average densities of the planet and the object
respectively, and
provide the average densities of the planet and the object
respectively, and 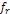 is a constant, where
is a constant, where 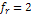 for the case of a rigid satellite and
for the case of a rigid satellite and 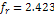 for the case of a fluid satellite. Relying only on Newtonian
gravitation, it is
difficult to explain the range of radii where both rings and
satellites are observed
to coexist (for example, in the range starting with the Encke gap,
which contains the satellite Pan,
up to Pandoraís
radius of orbit between the A ring
and the F ring). The
intermingling of rings and satellites
can be explained relatively easily via the UG theory, as the
potential energy of the object due to the contribution of SHP
groups contains cosine terms that oscillate as a function of the
inverse of their distance from the object. In
the range of radii in the vicinity of the classical Roche limit, or
for the case of a fluid satellite. Relying only on Newtonian
gravitation, it is
difficult to explain the range of radii where both rings and
satellites are observed
to coexist (for example, in the range starting with the Encke gap,
which contains the satellite Pan,
up to Pandoraís
radius of orbit between the A ring
and the F ring). The
intermingling of rings and satellites
can be explained relatively easily via the UG theory, as the
potential energy of the object due to the contribution of SHP
groups contains cosine terms that oscillate as a function of the
inverse of their distance from the object. In
the range of radii in the vicinity of the classical Roche limit, or
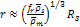 ,
the additional oscillating terms create sub-zones in which the tidal
forces of Saturn prevent
additional coalescence, where planetary rings
can consequently be retained. These sub-zones are separated by a
second set of sub-zones in which the tidal forces enhance
coalescence, or are simply too weak to prevent it, possibly
resulting in the formation of a satellite and in the consumption
and/or ejection of the enclosed ring material. Therefore, in this
range of radii, a series of narrow rings and small satellites
can coexist. However, the amplitudes of the SHP-generated
oscillations are relatively small compared with the amplitude of the
potential energy contributed by the planetís ordinary matter.
Consequently, the oscillations affect the process by which matter
coalesces to form a satellite mainly in the vicinity of the
classical Roche limit. Outside this range of radii, the UG-based
model becomes consistent with the results of the classical Roche
model. Hence, in
agreement with the Newtonian theory,
no satellites can formbelow the vicinity of ,
the additional oscillating terms create sub-zones in which the tidal
forces of Saturn prevent
additional coalescence, where planetary rings
can consequently be retained. These sub-zones are separated by a
second set of sub-zones in which the tidal forces enhance
coalescence, or are simply too weak to prevent it, possibly
resulting in the formation of a satellite and in the consumption
and/or ejection of the enclosed ring material. Therefore, in this
range of radii, a series of narrow rings and small satellites
can coexist. However, the amplitudes of the SHP-generated
oscillations are relatively small compared with the amplitude of the
potential energy contributed by the planetís ordinary matter.
Consequently, the oscillations affect the process by which matter
coalesces to form a satellite mainly in the vicinity of the
classical Roche limit. Outside this range of radii, the UG-based
model becomes consistent with the results of the classical Roche
model. Hence, in
agreement with the Newtonian theory,
no satellites can formbelow the vicinity of 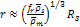 ,
while beyond this range,
planetary rings coalesce into satellites
over time. However, contrary to the prediction of Newtonís
theory, in the vicinity
of ,
while beyond this range,
planetary rings coalesce into satellites
over time. However, contrary to the prediction of Newtonís
theory, in the vicinity
of 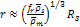 ,
rings and small satellites
may coexist. ,
rings and small satellites
may coexist. 12
As matter of fact, the UG theory leads to the conclusion that the
rings are composed almost entirely of tight spirals. 13As will be shown, the effect of
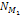 and
and 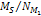 on the morphology is
relatively small, therefore reducing the minimum number of
independent variables required to explain and emulate the rings of
Saturn to five.
on the morphology is
relatively small, therefore reducing the minimum number of
independent variables required to explain and emulate the rings of
Saturn to five. 14
Equation 5-3b can be proven with the aid of the centrifugal force
equation 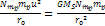 ,
leading to ,
leading to 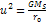 .
Subsequently, substituting .
Subsequently, substituting 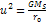 in the kinetic energy term on the left side of equation 5-3b proves
this equation. Note that the orbiting object velocity
in the kinetic energy term on the left side of equation 5-3b proves
this equation. Note that the orbiting object velocity 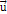 is non relativistic, and that observations have established that the
deviations of the motion of Saturnís
rings objects and satellites
from Keplerís laws
are minimal, thus the contribution of the SHPs to the overall force
must be very small. Therefore, the non-relativistic centrifugal
force, which neglects the contribution of the SHPs to the overall
amplitude of the force, should provide a good approximation.
is non relativistic, and that observations have established that the
deviations of the motion of Saturnís
rings objects and satellites
from Keplerís laws
are minimal, thus the contribution of the SHPs to the overall force
must be very small. Therefore, the non-relativistic centrifugal
force, which neglects the contribution of the SHPs to the overall
amplitude of the force, should provide a good approximation. 15
In mathematical terms, ordinary matter affects the location of the
minima through the  term in the denominator of equation 2-1-42. As
term in the denominator of equation 2-1-42. As ,
the ordinary matter effect is significantly smaller than ,
the ordinary matter effect is significantly smaller than 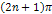 for any case where
for any case where 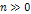 ,
and diminishes as ,
and diminishes as  increases. At low
increases. At low  indices, the influence of ordinary matter is limited to shifting the
minima locations, causing a relatively mild distortion to the
overall ring structure. Inclusion of the ordinary matter
contribution in the UG calculations requires the use of a wide range
of energy scales in the two dimensional maps, which would overwhelm
the SHP contribution,
flattening the oscillations contributed by the SHP
groups to the point where the local maxima and minima become almost
indistinguishable. Therefore, the term
indices, the influence of ordinary matter is limited to shifting the
minima locations, causing a relatively mild distortion to the
overall ring structure. Inclusion of the ordinary matter
contribution in the UG calculations requires the use of a wide range
of energy scales in the two dimensional maps, which would overwhelm
the SHP contribution,
flattening the oscillations contributed by the SHP
groups to the point where the local maxima and minima become almost
indistinguishable. Therefore, the term 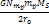 was left out.
was left out. 16
Grayscale was applied to indicate the energy level at any given
display point, where darker shades represent higher potential energy
levels. 17
Note that the multiplication by 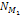 in equation 5-4 does not affect the morphology
of the ring system,
reducing the number of independent parameters needed to five.
in equation 5-4 does not affect the morphology
of the ring system,
reducing the number of independent parameters needed to five. 18
This approximate value was obtained via trial and error, by simply
calculating the map of the various rings to determine the range of
values that correctly provided areas of abundant fine structure and
areas of little or no fine structure. 19
Note that Cassini
reported the existence of ultra-fine structure with kilometer scale
in the inner A ring,
which may require an additional third SHP
group with a velocity 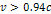 .
An extremely rapid SHP
group may also explain the structure of Saturnís
dusty rings, such as the G and E rings. .
An extremely rapid SHP
group may also explain the structure of Saturnís
dusty rings, such as the G and E rings. 20
Note that it is possible that the mass of the superheavy particles
in the second group may differ slightly from 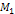 . . 21
A tilting effect was achieved by reducing the scale of the  axis.
axis. 22
The resolution of the  axis was reduced by a factor of ten relative to the
axis was reduced by a factor of ten relative to the 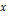 axis in order to mimic the tilting of the ring plane relative to the
viewing angle of the telescope in figure 5-5b.
axis in order to mimic the tilting of the ring plane relative to the
viewing angle of the telescope in figure 5-5b. 23Figure 5-6b is displayed in
lower resolution relative to figure 5-6a, in order to fit with the
resolution of the observed ring. 24
For a more detailed analysis, see Chapter VI. 25A
good analogy to this process is the Archimedes screw pump, which
consists of a screw rotating inside a hollow pipe, historically used
to transfer water from a low-lying body of water into irrigation
ditches. As the screw rotates endlessly around its axis without any
forward motion, it elevates a volume of water by pushing it forward
along its axis of rotation. In the present case of the orbiting
ring object, the SHP
contribution to the force acting on the object is small relative to
the Newtonian contribution of the planetís ordinary matter.
Therefore, the rotating spiral is powerful enough to replenish the
minute amount of energy lost by the ring particles in less than 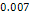 seconds it takes the SHP
groups to complete a full rotation around the center of Saturn,
but not sufficiently powerful to advance the particles outwards. A
more complete analogy will be provided in Chapter VI for the case of
galaxies, where the
rotating spirals demonstrate
sufficient strength to pump out ordinary matter in the form of
galactic wind.
seconds it takes the SHP
groups to complete a full rotation around the center of Saturn,
but not sufficiently powerful to advance the particles outwards. A
more complete analogy will be provided in Chapter VI for the case of
galaxies, where the
rotating spirals demonstrate
sufficient strength to pump out ordinary matter in the form of
galactic wind. 26
The time 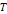 it takes the SHP groups
to complete a full rotation around Saturn
center is approximately
it takes the SHP groups
to complete a full rotation around Saturn
center is approximately 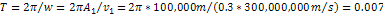 seconds.
seconds. 27
A good analogy can be found in sound waves, where the amplitude and
frequency of the sound, rather than the exact phase at a given
moment, determine our perception of its loudness and pitch. 28The two dimensional images do
not contain the term 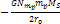 for the reasons discussed above.
for the reasons discussed above.
29In order to
demonstrate how the spirals are related to the potential energy
waveforms, the three waveforms are overlayed with two dimensional
calculated images of the potential energy of the given object. This
requires displaying the waveforms and the images of the calculated
potential energy using the same 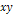 coordinates. Therefore, the equations of the waveforms were
multiplied by respective factors of
coordinates. Therefore, the equations of the waveforms were
multiplied by respective factors of 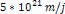 , ,
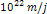 and
and 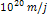 ,
and shifted down by ,
and shifted down by  , ,
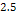 and
and 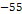 units (units of
units (units of 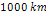 )
respectively. The
method used to calculate the approximate number of SHPs in each
group ( )
respectively. The
method used to calculate the approximate number of SHPs in each
group (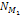 and
and 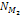 )
will be described later in the chapter. )
will be described later in the chapter. 30A clear demonstration,
displayed in Figure 5-9b, was created using increased values of 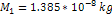 , ,
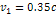 and a reduced radius of
and a reduced radius of 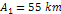 ,
where the point ,
where the point  was layered only when
was layered only when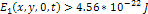 .
These values do not fit the Saturian ring structure and are only
intended to provide a more vivid display of spoke features. .
These values do not fit the Saturian ring structure and are only
intended to provide a more vivid display of spoke features. 31
It is often the case with optical patterns that to be observed they
must adhere to certain optimal geometrical conditions. For example,
holograms may require a relatively narrow range of viewing and
illumination angles, as well as a narrow range of wavelengths for
the illuminating light. The quality of holograms also depends on
the density as well as other properties of the filmís
emulsion. Slight variations in any of these parameters may make the
difference between a sharp image and no image at all. 32
Similar dynamics have been observed
in the D ring, where D72
was reported to have transformed from a bright, narrow ringlet of
less than 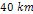 to a broad and diffuse structure which extends over
to a broad and diffuse structure which extends over 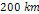 during the 25 years that passed between NASAís Voyager
and Cassini missions. In
addition, the F ring is
reported to be dynamic, and has changed significantly since the
Voyager mission.
during the 25 years that passed between NASAís Voyager
and Cassini missions. In
addition, the F ring is
reported to be dynamic, and has changed significantly since the
Voyager mission. 33Note that if either one of  or
or  is known, the other can be easily derived via the known ratio of
is known, the other can be easily derived via the known ratio of 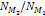 34
As the influence of superheavy particles
reduces drastically above the SHP
oscillation range (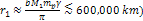 ,
the SHP effect on
satellites farther than
Lapetus is not significant. ,
the SHP effect on
satellites farther than
Lapetus is not significant. 35
Since the purpose of the present discussion is to estimate the
number of superheavy particles,
a quasi-relativistic, rather than a complete relativistic
correction, was made by the inclusion of 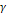 in the force equation.
in the force equation. 36
The calculations in this section use the following values: 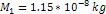 , ,
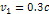 , ,
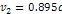 , ,
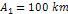 , ,
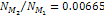 . .
|



