Section III-1: The
UG Morphology Model- The Non-Relativistic Approach
The goal of this chapter is to develop the equations and tools
required for the application of the UG theory to the quantitative
analysis of large astronomical objects, such as galaxies and
nebulae. For convenience, the reader should keep in mind that
throughout this chapter, the term ďgalaxyĒ will be
broadened to refer to galaxies as well as all types of nebulae, and
that the tools and equations developed here are general, and are not
limited to galaxies and nebulae. The same tools and equations will
be applied in later chapters for the analysis of cosmic voids,
planetary rings, as well as to additional astronomical phenomena.
The UG theory is rooted in the assumption that the dominant
superheavy particles in a galaxy are produced in areas of extremely
high pressure and temperature, and are therefore most likely to be
situated at the center, or in orbits at close proximity to the center
of the galactic bulge. Each of these superheavy particles can be
viewed as part of a point-like group, where a ďgroupĒ is
defined as either a single SHP, or a tight group of SHPs of the same
mass that share the same orbit, location and velocity.1
Note that the superheavy particles within a single group, or within
different SHP groups, are prevented from collapsing into each other
by the UG rejection zones generated between them.2
Although there is no reason to assume that a galaxy center should
contain only a single type of SHP, it will be demonstrated via the UG
theory that even simple configurations can explain a large portion of
the observed galactic morphologies. Figure 3-1 provides a schematic
of the two simplest interactions possible between an object composed
of ordinary particles located within the galaxy plane at time
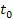 and superheavy particles arranged in either a single or binary
grouping. Figure 3-1a demonstrates the interaction between the
object and a single SHP group orbiting in circular motion of radius
and superheavy particles arranged in either a single or binary
grouping. Figure 3-1a demonstrates the interaction between the
object and a single SHP group orbiting in circular motion of radius
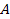 and constant angular velocity
and constant angular velocity
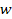 around the center of the galaxy. Figure 3-1b presents the
interaction between the object and a binary grouping of identical
superheavy particles in circular orbit of radius
around the center of the galaxy. Figure 3-1b presents the
interaction between the object and a binary grouping of identical
superheavy particles in circular orbit of radius
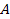 around the center of the galaxy.3
It will be demonstrated that the morphology of a galaxy is
determined mainly by the velocities and orbital radii of the dominant
SHP groups, while the size of the galaxy is determined mainly by the
mass of the dominant SHP type, and to a lesser degree by their
velocity.4
around the center of the galaxy.3
It will be demonstrated that the morphology of a galaxy is
determined mainly by the velocities and orbital radii of the dominant
SHP groups, while the size of the galaxy is determined mainly by the
mass of the dominant SHP type, and to a lesser degree by their
velocity.4

Figure
3-1: Provides a
schematic of the two simplest interactions possible between an object
composed of ordinary particles located within the galaxy plane at
time
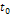 (represented by the red point) and SHPs arranged in either a single
or binary grouping. Figure 3-1a demonstrates the interaction between
the object and a single group orbiting in circular motion of radius
(represented by the red point) and SHPs arranged in either a single
or binary grouping. Figure 3-1a demonstrates the interaction between
the object and a single group orbiting in circular motion of radius
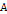 and constant speed around the center of the galaxy. Figure 3-1b
presents the interaction between the object and binary SHP
groups in circular motion of radius A around the galactic center. The
small open circles (cyan) denote the locations of the SHP
groups at time
and constant speed around the center of the galaxy. Figure 3-1b
presents the interaction between the object and binary SHP
groups in circular motion of radius A around the galactic center. The
small open circles (cyan) denote the locations of the SHP
groups at time
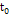 ,
while the full circles (blue) provide the given SHP
locations at time ,
while the full circles (blue) provide the given SHP
locations at time
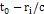 ,
where ,
where
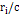 provides the time required for the gravitational signal to travel
from the
provides the time required for the gravitational signal to travel
from the
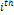 SHP group to the remote
particle at distance
SHP group to the remote
particle at distance
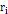 .
This delay will be demonstrated to play an important role in
creating the spiral structure. .
This delay will be demonstrated to play an important role in
creating the spiral structure.
For simplicity, the provided analysis of galactic morphology will be
guided by the following assumptions:
The unified
gravitational formula of the UG potential energy between two
interacting fundamental particles moving at non-relativistic speeds
relative to the center of the galaxy is given by equation 2-1-1,
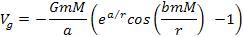
A
free-falling frame of reference that covers the entire spacetime of
a galaxy during the local time of the entire period of observation5
can be regarded as an inertial frame of reference. This assumption
is in line with the conclusion of the currently accepted
cosmological model, which states that the effects of general
relativity are negligible on the scale of galaxies and galactic
clusters.6
7
A convenient choice for an inertial frame is to set the origin of
the frame at the center of the galaxy. For the case of a flat
galactic disk, the
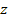 axis of the frame can be chosen to be perpendicular to the galactic
plane. This specific inertial frame of reference will be referred
to as frame
axis of the frame can be chosen to be perpendicular to the galactic
plane. This specific inertial frame of reference will be referred
to as frame
 . .
On their
journey from the galaxy to the observer on Earth, photons pass
through the gravitational fields of other galaxies. Therefore, the
trajectories of the photons may be bent by gravitation, causing a
distortion in the perceived morphology of the galaxy via
gravitational lensing. The present discussion will be limited to
cases where gravitational lensing is too small to significantly
affect the perceived morphology of the galaxy.
Radiation redshift, due either to the speed of the observed galaxy
relative to the observer, or due to gravitation, affects the
wavelength and frequency of galactic radiation, but not the perceived
morphology of the galaxy. In addition, the second and third
assumptions allow the analysis of galactic morphology to ignore
possible distortions due to external gravitational effects on the
galaxy, on the observer, or on the spacetime anywhere along the path
of the radiation emitted by the galaxy and intercepted by the
observer, and to instead rely exclusively on the UG theory and on
special relativity within the limits of the given galaxy.8
To further simplify the analysis, the discussion will be restricted
to galaxies with the following properties:
The galaxy center contains either a single SHP group or a binary
grouping in circular orbit of radius
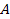 around the galaxy center, where the group(s) consist of a single
type of superheavy particles of identical mass.
around the galaxy center, where the group(s) consist of a single
type of superheavy particles of identical mass.
The observer views the galaxy face-on.
Due to its rotation, the galaxy is confined to a flat disk with
negligible depth, designated as the
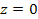 plane of the inertial frame
plane of the inertial frame
 . .
Tidal forces and other external influences of nearby galaxies are
relatively small and can be ignored.
The diameter of the galaxy is very small relative to its distance
from the observer.
The orbiting objects are composed of ordinary matter, and their size
is negligible relative to their radius of orbit around the galaxy
center.
The orbital radii of the objects are significantly greater than the
distance between the SHP group(s) and the center of the galaxy.
The above limitations serve to reduce mathematical complexity, and to
focus the discussion on the most important factors that influence
galaxy morphology. There is nothing preventing the use of the same
tools developed here for the case of more complex galaxies that may
involve multiple SHP types contained in a number of groups, or for
galaxies that are viewed at different orientations (other than
face-on observation), or for cases where the galaxies are influenced
by external galaxies, or where the orbiting matter is composed of
SHPs as well as ordinary particles. The same types of tools can also
be used for the analysis of stellar and planetary systems, and will
be applied in Chapter V for the more complex analysis of Saturnís
rings.
In principle, the effective distance photons travel on their way from
the emitting atom within the galaxy toward the observer depends on
the location of the galaxy and on its relative velocity compared to
the observer as well as on the velocity and the location of the
emitting atom within the galaxy.9
Given assumptions 5, 6 and 8 we are assured that the velocity of the
particle that emitted an observed photon is perpendicular to the
photonís path. Therefore, regardless of the position or the
velocity of the emitting atoms within the galaxy disk at the time of
the photon emission, the effective distance between the emitting
atoms and the observer and the time it take the photons to reach the
observer are virtually identical and depend only on the distance and
velocity of the galaxy relative to the observer.10
Furthermore, assumptions 5 and 8 and the observation that the object
within the galactic disk move at non-relativistic velocities relative
to the galactic center, assure us that for all practical purposes,
any two photons that are detected simultaneously by the observer have
traveled the same distance and the same amount of time regardless of
the location from which they were emitted within the given galaxy.11
Galaxy morphology is typically determined by the spatial
distribution of the radiation emitted by ordinary matter within the
galaxy that is detected by the observer. The observerís
perception of galactic shape is strongly affected by the contrast
between areas of high radiation (and therefore, high brightness) and
areas of low radiation. The amount of radiation emitted by any given
region of a galaxy is related to the density of ordinary matter
within this region. The density of ordinary matter, and thus the
radiation level, is expected to be higher at locations where the
overall energy of orbiting ordinary matter has a local minimum.
Thus, identifying the local minima, predominantly those that produce
sharp brightness contrast to their background, will provide the
theoretical morphology of the galaxy.
The task at hand is to use the UG equation to analyze the energy
patterns formed by the combined effect of superheavy particles
(either stationary or rotating) at the central core of a galaxy and
the surrounding ordinary matter; In particular, to identify the
minimum points, contours and arcs, and how they change over time.
Establishing this task will facilitate in confirming the initial
hypothesis, that in all or most cases, the observed shape and
properties of a galaxy can be explained by the configuration of its
dominant superheavy particles.
The following equations, developed to identify
the local minima, will initially use the symbols
 for the speed of light and
for the speed of light and
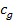 for the speed of gravitation. The
assumption that the propagation speed of gravity is equal to the
speed of light will only be made at a later stage. As gravity
propagates at a finite speed
for the speed of gravitation. The
assumption that the propagation speed of gravity is equal to the
speed of light will only be made at a later stage. As gravity
propagates at a finite speed
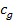 ,
the gravitational signal requires time to reach the orbiting object.
Consider an object with an orbital radius of ,
the gravitational signal requires time to reach the orbiting object.
Consider an object with an orbital radius of
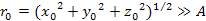 .
The gravitational signal (or graviton) detected by the orbiting
object at .
The gravitational signal (or graviton) detected by the orbiting
object at
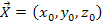 at time
at time
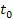 in frame S
was actually emitted by a superheavy particle at the S
position
in frame S
was actually emitted by a superheavy particle at the S
position
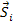 at an earlier time
at an earlier time
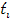 ,
where the emittance time ,
where the emittance time
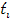 and location
and location
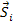 are related by
are related by
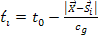 .
The period .
The period
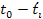 presents a delay that increases with the distance
presents a delay that increases with the distance
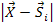 . .
The velocity of matter located in the galaxy
halo is typically non-relativistic at
about a few hundred
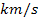 .
For non-relativistic SHP groups with
velocities .
For non-relativistic SHP groups with
velocities
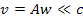 ,
the entire calculation can take place in the rest frame of the center
of the galaxy. In this frame, the potential energy of an object
composed of ,
the entire calculation can take place in the rest frame of the center
of the galaxy. In this frame, the potential energy of an object
composed of
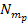 ordinary particles located in the galaxy halo
is given approximately by
ordinary particles located in the galaxy halo
is given approximately by
Equation
3-1-1
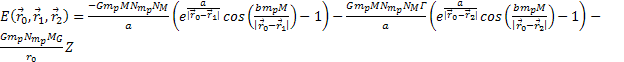
where
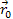 denotes the location of the object at time
denotes the location of the object at time
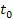 ,
and ,
and
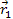 and
and
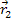 represent the locations of the two groups of superheavy particles
at the time they emitted the gravitational signals intercepted by the
object at time
represent the locations of the two groups of superheavy particles
at the time they emitted the gravitational signals intercepted by the
object at time
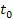 .
For simplicty, the total mass of ordinary matter in the galaxy,
given by .
For simplicty, the total mass of ordinary matter in the galaxy,
given by
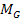 ,
is assumed to be homogeneously distributed around the galaxy center
within a radius ,
is assumed to be homogeneously distributed around the galaxy center
within a radius
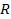 .
The value .
The value
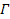 is a positive number defined as the ratio between the number of SHPs
in group 2 and group 1. Setting
is a positive number defined as the ratio between the number of SHPs
in group 2 and group 1. Setting
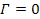 for the case of a single SHP group rotating
around the center of the galaxy, and
for the case of a single SHP group rotating
around the center of the galaxy, and
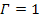 for the case of identical binary groups, will allow the same set of
equations to cover both scenarios. In the case of binary groups
where
for the case of identical binary groups, will allow the same set of
equations to cover both scenarios. In the case of binary groups
where
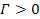 ,
both groups are assumed to follow a circular orbit of radius ,
both groups are assumed to follow a circular orbit of radius
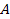 around the galaxy center with the same constant speed
around the galaxy center with the same constant speed
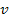 .
It is further assumed that the two SHP groups
and the galaxy center are co-linear,12
The last term of 3-1-1, which represents the interaction between the
ordinary matter of the galaxy and the ordinary matter of the orbiting
object includes the variable .
It is further assumed that the two SHP groups
and the galaxy center are co-linear,12
The last term of 3-1-1, which represents the interaction between the
ordinary matter of the galaxy and the ordinary matter of the orbiting
object includes the variable
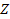 ,
defined as ,
defined as
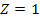 when
when
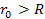 ,
and as ,
and as
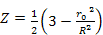 when
when
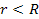 . .
The orbiting stars and interstellar gas in a galaxy are expected to
gravitate strongly toward regions of lower potential energy, creating
areas of increased density in their vicinity. As
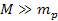 ,
the interaction between the galaxyís ordinary matter and the
object provides a relatively smooth and slow-changing potential
energy curve compared with the rapid oscillations of the potential
energy of the object due to its interaction with the galaxyís
SHPs. Therefore, as demonstrated in figure 3-2, it is likely that
even if the contribution of a galaxyís ordinary matter to the
potential energy of an object is significantly larger than the
overall contribution of the galaxyís superheavy particles, the
locations of the potential energy minima of the interaction are
determined almost entirely by the SHP masses, velocities and
locations, while the influence of the galaxyís ordinary matter
on the minima locations is almost negligible.13 ,
the interaction between the galaxyís ordinary matter and the
object provides a relatively smooth and slow-changing potential
energy curve compared with the rapid oscillations of the potential
energy of the object due to its interaction with the galaxyís
SHPs. Therefore, as demonstrated in figure 3-2, it is likely that
even if the contribution of a galaxyís ordinary matter to the
potential energy of an object is significantly larger than the
overall contribution of the galaxyís superheavy particles, the
locations of the potential energy minima of the interaction are
determined almost entirely by the SHP masses, velocities and
locations, while the influence of the galaxyís ordinary matter
on the minima locations is almost negligible.13
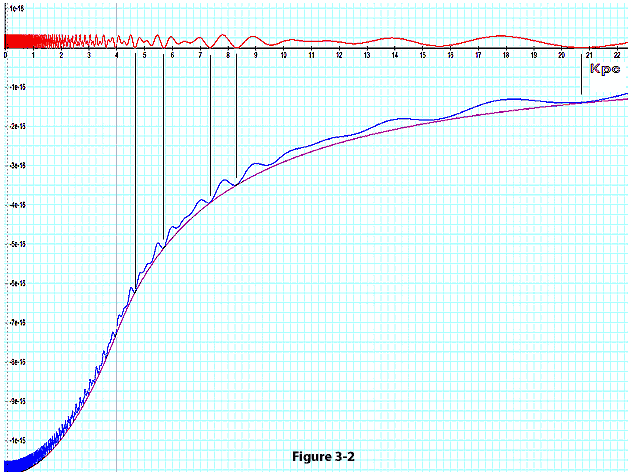
Figure
3-2: Presents the
potential energy of a single ordinary particle of mass
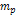 as a function of its distance from the galaxy center. The red curve
provides the potential energy due to the influence of two stationary
SHP groups, each
containing 54 SHPs of mass
as a function of its distance from the galaxy center. The red curve
provides the potential energy due to the influence of two stationary
SHP groups, each
containing 54 SHPs of mass
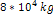 ,
located at a distance of ,
located at a distance of
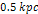 from the galaxy center. The two groups are assumed to be positioned
in a linear alignment with the galactic center, on either side of the
center. The purple curve provides the potential energy of the
particle due to
from the galaxy center. The two groups are assumed to be positioned
in a linear alignment with the galactic center, on either side of the
center. The purple curve provides the potential energy of the
particle due to
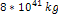 of ordinary matter distributed homogeneously within a sphere of
of ordinary matter distributed homogeneously within a sphere of
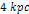 centered around the galaxy center. The combined effect of both SHP
groups and of the galaxyís ordinary matter is demonstrated by
the blue curve. The black vertical lines indicate the deepest minima
contours between
centered around the galaxy center. The combined effect of both SHP
groups and of the galaxyís ordinary matter is demonstrated by
the blue curve. The black vertical lines indicate the deepest minima
contours between
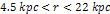 ,
demonstrating that the minima occur almost precisely at the same
distances, whether or not the effect of the ordinary matter is
included. Ordinary matter is expected to be concentrated in the
vicinity of the local minima, with higher densities at the deeper
minima. Although the potential energy in this example is dominated
by the objectís interaction with ordinary matter (at least at ,
demonstrating that the minima occur almost precisely at the same
distances, whether or not the effect of the ordinary matter is
included. Ordinary matter is expected to be concentrated in the
vicinity of the local minima, with higher densities at the deeper
minima. Although the potential energy in this example is dominated
by the objectís interaction with ordinary matter (at least at
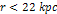 ),
the galactic ordinary matter is demonstrated to have little influence
on the positions of substantial minima. Note, however, that shallow
minima contributed by the two SHP
groups may become washed out by the contribution of the galactic
ordinary matter. For example, the two shallow minima between ),
the galactic ordinary matter is demonstrated to have little influence
on the positions of substantial minima. Note, however, that shallow
minima contributed by the two SHP
groups may become washed out by the contribution of the galactic
ordinary matter. For example, the two shallow minima between
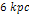 and
and
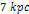 , and the two minima between
, and the two minima between
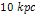 and 14
and 14
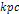 in the red curve do not remain minima after the inclusion of the
ordinary matter contribution, as shown by the blue curve.
in the red curve do not remain minima after the inclusion of the
ordinary matter contribution, as shown by the blue curve.
Therefore, locations of high density matter would not be notably
affected by the Newtonian term in equation 3-1-1, and can
consequently be found in the minima of the following equation:
Equation
3 - 1 - 2
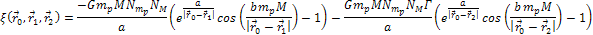
First, the locations at which the gravitational signal was emitted
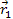 and
and
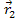 must be calculated. Due to the finite speed of gravitation, the
object located at
must be calculated. Due to the finite speed of gravitation, the
object located at
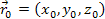 at time
at time
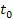 in the inertial frame
in the inertial frame
 simultaneously receives the UG gravitational signals that were
emitted by the two respective groups at earlier
simultaneously receives the UG gravitational signals that were
emitted by the two respective groups at earlier
 times
times
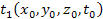 and
and
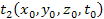 by the two respective groups, which were located at
by the two respective groups, which were located at
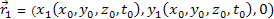 and
and
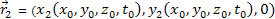 at the time of the signal emissions. Therefore,
at the time of the signal emissions. Therefore,
Equation
3 -1Ė3a
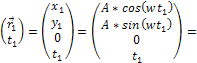
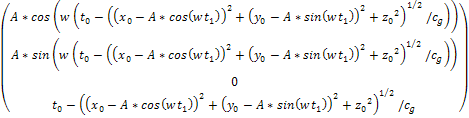
and
Equation
3Ė1-3b
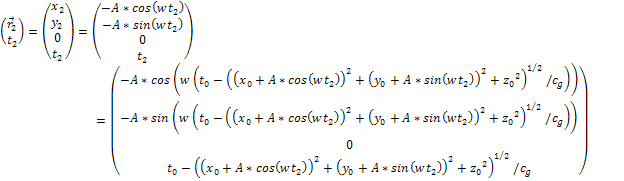
Therefore
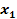 and
and
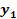 are explicit functions of
are explicit functions of
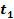 ,
and their dependency on ,
and their dependency on
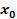 , ,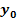 , ,
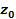 and
and
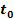 is only through
is only through
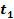 .
Similarly, .
Similarly,
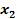 and
and
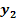 are explicit functions of
are explicit functions of
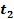 ,
and thus are indirectly dependent on ,
and thus are indirectly dependent on
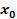 , ,
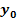 , ,
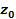 and
and
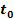 . .
The minus signs preceding the terms
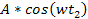 and
and
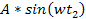 in the equation for the second group are due to the requirement that
at any given
in the equation for the second group are due to the requirement that
at any given
 time, the two groups and their common center of mass are drawn along
a straight line, and are thus half a cycle apart. Since the
distances between the orbiting object and the two groups in the
inertial frame
time, the two groups and their common center of mass are drawn along
a straight line, and are thus half a cycle apart. Since the
distances between the orbiting object and the two groups in the
inertial frame
 are usually different, the amount of time required for the
gravitational signal to propagate from each group to the object will
vary, and frequently
are usually different, the amount of time required for the
gravitational signal to propagate from each group to the object will
vary, and frequently
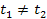 .
However, as the maximum difference between the two groups is .
However, as the maximum difference between the two groups is
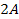 , ,
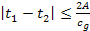 . .
The
values
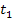 and
and
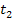 are essential for conducting successful calculations of galactic
shapes and properties. Unfortunately, finding a direct analytical
solution for equations 3-1-3a and 3-1-3b is not that simple. Instead,
it is more practical to use an iterative approach, where the first
order of titration is given by
are essential for conducting successful calculations of galactic
shapes and properties. Unfortunately, finding a direct analytical
solution for equations 3-1-3a and 3-1-3b is not that simple. Instead,
it is more practical to use an iterative approach, where the first
order of titration is given by
Equation
3-1-4
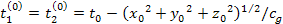
Followed
by
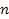 additional titrations,
additional titrations,
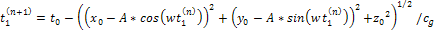
and for the second group,
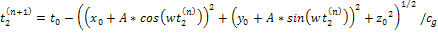
At
the final stage, the emission times in frame
 are assigned the values
are assigned the values
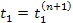 and
and
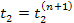 .
For the following examples, it is assumed that in the case of .
For the following examples, it is assumed that in the case of
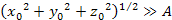 ,
a single iteration can provide sufficiently accurate results.
Therefore, ,
a single iteration can provide sufficiently accurate results.
Therefore,
Equation
3 -1Ė5
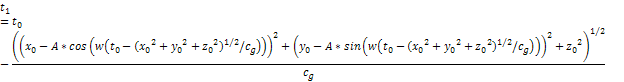
and
Equation
3-1-6
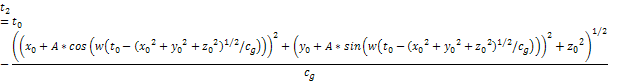
Given the small value of the constant
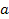 (
(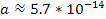 ),
at galactic distance ranges the exponent terms ),
at galactic distance ranges the exponent terms
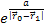 and
and
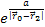 can be replaced by
can be replaced by
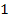 .
As we are looking for the minima of equation 3-1-1, the highest
density of matter is expected to be concentrated in the vicinity of
the deepest minima, which occur at the lowest points of the following
equation: .
As we are looking for the minima of equation 3-1-1, the highest
density of matter is expected to be concentrated in the vicinity of
the deepest minima, which occur at the lowest points of the following
equation:
Equation
3-1-7
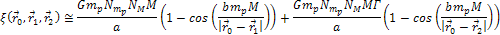
Note
that at the limit
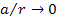 , ,
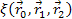 is always greater than or equal to zero. With
is always greater than or equal to zero. With
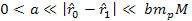 and and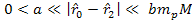 ,
the lowest minima, and therefore the highest density distribution,
will occur in the vicinity of the locations ,
the lowest minima, and therefore the highest density distribution,
will occur in the vicinity of the locations
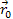 that comply with
that comply with
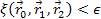 ,
where ,
where
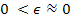 .
This will happen at locations where both cosine terms are
simultaneously equal to .
This will happen at locations where both cosine terms are
simultaneously equal to
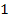 .
Note that at higher levels of potential energy, the discussion can
be extended to areas of lower density by simply allowing a range of
higher values for .
Note that at higher levels of potential energy, the discussion can
be extended to areas of lower density by simply allowing a range of
higher values for
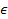 .
This method of dividing the range of possible potential energies
into slices of .
This method of dividing the range of possible potential energies
into slices of
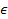 values will be used in the next few chapters to provide the two
dimensional contour maps (or isophotes) of the
potential energy profile of a galaxy, and to demonstrate the
resulting features, such as rings or spiral arms.
values will be used in the next few chapters to provide the two
dimensional contour maps (or isophotes) of the
potential energy profile of a galaxy, and to demonstrate the
resulting features, such as rings or spiral arms.
III-2: The UG
Morphology Model- The Relativistic Approach
The dynamic calculations required for the case of a
group of superheavy particles moving at
relativistic velocity relative to the inertial frame
of reference are somewhat more complex. Force and potential
energy are not invariant under Lorentz transformations, and may
change form when viewed in different inertial frames moving at
relativistic velocities relative to each other. Therefore, a force
law must be defined in a specific inertial frame. Prior to
Einsteinís special theory of relativity, Coulombís law
was known to accurately provide the electromagnetic force applied on
a test charge moving at any constant velocity only when the source
charge is at rest. When the source charge is not stationary relative
to the observer, it generates a magnetic field that applies an
additional force on the test particle, resulting in an overall force
which may or may not be a central force. Einstein showed that on the
basis of Coulombís force and special relativity alone, one can
generate a quantitative description of electric and magnetic
interactions between charges moving with arbitrary constant
velocities, and that what appears as a purely magnetic field, or as a
combination of an electric and a magnetic field, when viewed in one
coordinate system may be simply an electric (Coulomb) field when
viewed in another coordinate system. The key to developing all of
the electromagnetic kinematic and dynamic quantities is to use
Coulombís law only when the calculations are performed in the
inertial rest frame of the source charge. Thus, when the source
charge moves in respect to a given
 frame, the procedure entails the following three steps:
frame, the procedure entails the following three steps:
Step 1: The kinematic and dynamic parameters of the test particle
must first be transformed to frame
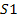 ,
in which the source charge is at rest. ,
in which the source charge is at rest.
Step 2: Apply the Coulomb force (or potential energy) equation to the
test particle.
Step 3: Transform the particlesí parameters back from frame
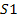 to frame
to frame
 . .
All
transformations are done via the Lorentz transformations (French,
1968). The realization that a force is not invariant under
Lorentz transformations, and that the same force that appears as a
central force from the point of view of one inertial frame may appear
as a non-central force and may be described by a different equation
form when viewed in a different inertial frame, led to the language
used in the second UG postulate given in Chapter II and repeated
below:
UG
Postulate II:
The
Unified Gravitational force is a force between a pair of particles.
When viewed at an inertial rest frame of one of the interacting
particles (the source particle), the unified gravitational force
applied on the second particle (the test particle) is predominantly a
central and conserving force that depends exclusively on the absolute
distance between the particles and on the product of their masses.
This
basic postulation further led, in conjunction with three additional
postulates (as well as the application of the principle of Occamís
Razor), to a family of possible gravitational equations, where
equation 2-1-1 was selected as the simplest potential energy equation
that complies with the given postulates. An additional assumption was made at the beginning of this
chapter, stating that a free-falling frame of reference that covers
the entire spacetime of a given galaxy during the local time of the
observation can be regarded as an inertial frame throughout the
galaxy, with the exception of the immediate vicinity of collapsing
stars.Under the
provided postulates and assumptions, the galaxy can be correctly
analyzed via equation 2-1-5 and special relativity. As this equation
is only valid in the rest frame of a source particle, calculating the
UG force applied to a moving test particle requires a procedure
similar to the three-step procedure described above for the case of
the Coulomb force. However, there is an important difference: the
Coulomb force depends on the particle charges, which are the same in
any frame of reference. The UG force equation, however, depends on
the particle masses, which are not invariant under the Lorentz
transformations.
Therefore, the mass of the test particle
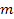 in equation 2-1-5 provides the mass as viewed by the source particle,
which is equal to
in equation 2-1-5 provides the mass as viewed by the source particle,
which is equal to
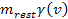 ,
where ,
where
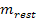 is the rest mass of the test particle and
is the rest mass of the test particle and
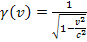 . The same procedure can be used to calculate the potential energy
of the test particle via equation 2-1-1.
. The same procedure can be used to calculate the potential energy
of the test particle via equation 2-1-1.
Therefore, in order to assess the UG effect applied by either SHP
group on the object, the calculation must take place in the inertial
frame where the group is momentarily at rest, denoted by
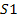 for the first group and
for the first group and
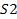 for the second group. The relativistic velocity of the object
relative to the SHP groups can theoretically result from either the
relativistic velocities of either one of the SHP groups
for the second group. The relativistic velocity of the object
relative to the SHP groups can theoretically result from either the
relativistic velocities of either one of the SHP groups
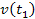 and
and
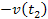 ,
or from the relativistic velocity of the object ,
or from the relativistic velocity of the object
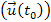 relative
to the center of the galaxy, or from both. However, matter in the
galaxy disk and halo has typically been observed to travel at
non-relativistic velocities between relative
to the center of the galaxy, or from both. However, matter in the
galaxy disk and halo has typically been observed to travel at
non-relativistic velocities between
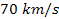 and
and
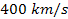 relative to the galactic center. Therefore, to the extent that
relativistic effects occur in galaxies, they must be attributed to
the relativistic velocities of their SHP groups. The speed of the
object thus becomes negligible compared with the relativistic speed
of the groups. In such cases, the relativistic velocity between a
given SHP group and a given objectcan be regarded as equal to the velocity of the group.
14
relative to the galactic center. Therefore, to the extent that
relativistic effects occur in galaxies, they must be attributed to
the relativistic velocities of their SHP groups. The speed of the
object thus becomes negligible compared with the relativistic speed
of the groups. In such cases, the relativistic velocity between a
given SHP group and a given objectcan be regarded as equal to the velocity of the group.
14
As
mentioned above, the UG force or potential energy equations 2-1-5 and
2-1-1 applied on an orbiting object are not invariant under Lorentz
transformation, and are assumed to be valid exclusively in the
inertial frame of the source at rest. For the relativistic case of a
galaxy consisting of two SHP groups, the UG equation of each group
must therefore be calculated in different inertial frames;
specifically, in inertial frame
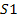 ,
where the first group is momentarily at rest at the ,
where the first group is momentarily at rest at the
 time
time
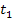 ,
and in inertial frame ,
and in inertial frame
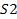 ,
where the second group is momentarily at rest at ,
where the second group is momentarily at rest at
 time
time
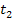 .
As a reminder, .
As a reminder,
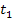 and
and
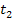 are the
are the
 time at which the respective groups emitted the gravitational
signals, which were simultaneously intercepted by the orbiting object
at
time at which the respective groups emitted the gravitational
signals, which were simultaneously intercepted by the orbiting object
at
 time
time
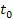 .
Time .
Time
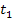 and
and
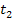 are given by equation 3-1-5 and 3-1-6 respectively.
are given by equation 3-1-5 and 3-1-6 respectively.
Calculating the potential energy at any arbitrary point
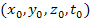 in the
in the
 inertial frame requires the Lorentz transformation of coordinates
from frame
inertial frame requires the Lorentz transformation of coordinates
from frame
 to frames
to frames
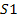 and
and
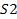 ,
where the UG equations 2-1-1 or 2-1-5 can be applied. The results
are then transformed back to the ,
where the UG equations 2-1-1 or 2-1-5 can be applied. The results
are then transformed back to the
 frame and combined to provide the overall potential energy or force.
frame and combined to provide the overall potential energy or force.
Starting with group 1, the first task is to calculate the magnitude
and direction of its velocity at
 time
time
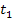 .
As assumed above, the coordinates of the first group within the .
As assumed above, the coordinates of the first group within the
 frame at the
frame at the
 emission time
emission time
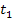 are given by
are given by
Equation
3-1-8
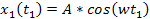 and
and
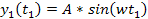 and
and
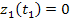
Consequently, the velocity of the SHP group within the
 frame is given by the derivative of equation 3-1-8,
frame is given by the derivative of equation 3-1-8,
Equation
3-1-9
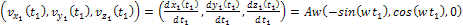
And
Equation
3-1-10
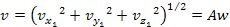
Note
that the angular velocity
 may be positive for counterclockwise rotation and negative for
clockwise rotation.
may be positive for counterclockwise rotation and negative for
clockwise rotation.
As discussed, applying the UG equation 2-1-1 requires the use of the
inertial frame where the source mass, in this case group 1, is
momentarily at rest. Note that as group 1 travels in circular motion
around the center of the galaxy, it is accelerating. Therefore, the
group will remain at rest in frame
 for only an infinitesimal period of time.
for only an infinitesimal period of time.
The distance
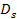 in frame
in frame
 between the frame
between the frame
 location of the orbiting object (
location of the orbiting object (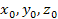 )
at the interception time )
at the interception time
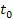 ,
and the frame ,
and the frame
 location of group 1
location of group 1
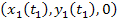 at the time of emission
at the time of emission
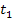 is given by
is given by
Equation
3-1-11
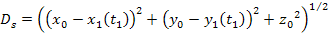
where
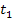 , ,
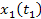 and
and
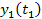 are given by equation 3-1-3a. Since group 1 is at rest in frame
are given by equation 3-1-3a. Since group 1 is at rest in frame
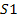 at
at
 time
time
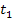 , ,
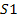 travels at a velocity given by equation 3-1-9 and 3-1-10 relative to
the inertial frame
travels at a velocity given by equation 3-1-9 and 3-1-10 relative to
the inertial frame
 .
Therefore, the distance .
Therefore, the distance
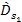 between the orbiting object and group 1 in the inertial frame
between the orbiting object and group 1 in the inertial frame
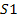 is almost always contracted. In calculating the distance
is almost always contracted. In calculating the distance
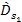 ,
it is more convenient to separately calculate the parallel and
vertical components of the velocity of group 1 within the rotation
plane ,
it is more convenient to separately calculate the parallel and
vertical components of the velocity of group 1 within the rotation
plane
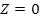 . .
The
component of the distance
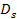 in the
in the
 frame that is parallel to the velocity of group 1 at time
frame that is parallel to the velocity of group 1 at time
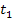 is given by
is given by
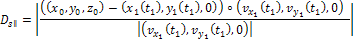
where
the value of
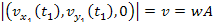 ,
as given by equation 3-1-10. Additionally, in circular motion the
velocity of the SHP group is perpendicular to the vector connecting
the rotating group to the center of the circle. Therefore, ,
as given by equation 3-1-10. Additionally, in circular motion the
velocity of the SHP group is perpendicular to the vector connecting
the rotating group to the center of the circle. Therefore,
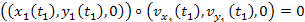 .
Consequently, .
Consequently,
Equation
3-1-12
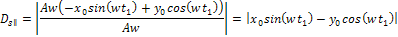
Since
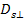 is defined to be perpendicular to
is defined to be perpendicular to
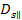 ,
and both are contained in the galaxy plane ,
and both are contained in the galaxy plane
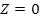 , ,
Equation
3-1-13
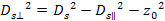
Since
the distance
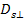 is perpendicular to the velocity of group 1, it is not altered by the
Lorentz transformation from the
is perpendicular to the velocity of group 1, it is not altered by the
Lorentz transformation from the
 frame to the
frame to the
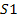 frame of reference. However, the parallel component
frame of reference. However, the parallel component
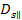 is contracted via division by
is contracted via division by
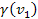 ,
where ,
where
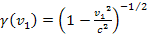 .
In addition, the velocity .
In addition, the velocity
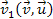 is the relative velocity between group 1 and the object, and
is the relative velocity between group 1 and the object, and
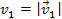 .
Therefore, .
Therefore,
Equation
3-1-14
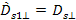 and
and
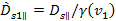
Using
equations 3-1-13 and 3-1-14
Equation
3-1-15
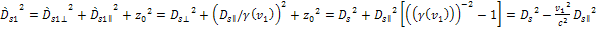
Substituting
equations 3-1-11 and 3-1-12 into equation 3-1-15,
Equation
3-1-16
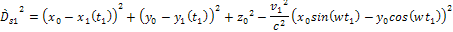
where
the
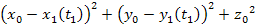 term is the same as in the non-relativistic case, and the term
term is the same as in the non-relativistic case, and the term
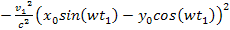 provides the relativistic distance contraction. Applying equation
3-1-8, and the fact that
provides the relativistic distance contraction. Applying equation
3-1-8, and the fact that
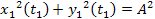 , ,
Equation
3-1-17a
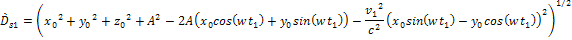
In
the case of a binary grouping, a phase shift of
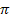 must be added to the operand of each cosine and sine term of the
second group and the time
must be added to the operand of each cosine and sine term of the
second group and the time
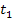 should be replaced by
should be replaced by
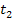 to provide
to provide
Equation
3-1-17b
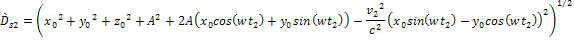
When
only the contribution of group 1 is taken into account, the objectís
energy as viewed at the
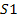 inertial frame (at a point denoted by the
inertial frame (at a point denoted by the
 coordinates
coordinates
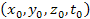 )
is given by )
is given by
Equation
3-1-18a
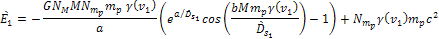
where
the mass of the objectís ordinary matter (in the
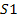 inertial frame) can be substituted by the product of its rest mass
inertial frame) can be substituted by the product of its rest mass
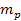 and
and
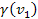 . .
At
 time
time
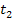 the second group travels at a velocity of
the second group travels at a velocity of
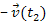 relative to the inertial frame
relative to the inertial frame
 .
Therefore, the objectís velocity relative to group 2 is .
Therefore, the objectís velocity relative to group 2 is
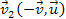 (and
(and
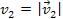 ).
When only the contribution of group 2 is taken into consideration, a
similar analysis of the energy of an object in the ).
When only the contribution of group 2 is taken into consideration, a
similar analysis of the energy of an object in the
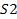 inertial frame of group 2 is provided by
inertial frame of group 2 is provided by
Equation
3-1-18b
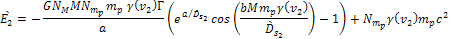
To
find the overall energy of the object in the
 frame, the energy due to group 1 in frame
frame, the energy due to group 1 in frame
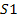 and the energy due to group 2 in frame
and the energy due to group 2 in frame
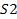 (including the objectís rest energy) must first be identified
and transformed via Lorentz transformations, i.e.
(including the objectís rest energy) must first be identified
and transformed via Lorentz transformations, i.e.
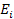 = =
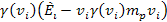 ,
where ,
where
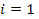 or or
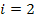 .
The total energy .
The total energy
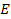 can then be derived by adding
can then be derived by adding
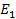 and
and
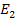 ,
and since the energy derived from the objectís rest mass was
counted twice (once in either inertial frame), it must also be
subtracted once. In addition, as stated above, the velocity ,
and since the energy derived from the objectís rest mass was
counted twice (once in either inertial frame), it must also be
subtracted once. In addition, as stated above, the velocity
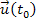 of the object in frame
of the object in frame
 (typically less than
(typically less than
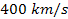 )
is non-relativistic, and therefore in the case of relativistic
superheavy particles, )
is non-relativistic, and therefore in the case of relativistic
superheavy particles,
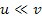 .
Consequently, .
Consequently,
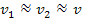 and
and
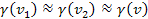 .15
This approximation serves to simplify the math, as it removes the
need to know the exact direction of the velocity .15
This approximation serves to simplify the math, as it removes the
need to know the exact direction of the velocity
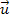 at the
at the
 time
time
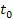 ;
however, it also eliminates the non-relativistic kinetic energy of
the object, which must therefore be added back into the equation.
Taking the above, as well as the contribution of the influence of
non-relativistic ordinary matter into consideration, the overall
energy of the object in the ;
however, it also eliminates the non-relativistic kinetic energy of
the object, which must therefore be added back into the equation.
Taking the above, as well as the contribution of the influence of
non-relativistic ordinary matter into consideration, the overall
energy of the object in the
 inertial frame is given by
inertial frame is given by
Equation
3-1-19
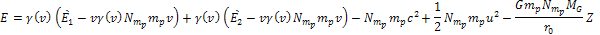
Using
the identity
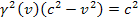 leads to
leads to
Equation
3-1-20
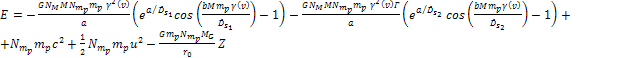
Recall
that the morphology of a galaxy is determined by the distribution of
the radiation detected by an observer. The observerís
perception of morphology is strongly affected by the areas of high
radiation (or brightness), and by their contrast with the background
level of brightness. The amount of radiation emitted by any given
area of the galaxy is largely related to its size and the density of
its ordinary matter. The density, however, is expected to be higher
at locations where the total energy of the object
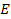 has a local minimum, particularly at the relatively deep minima,
which are significantly lower than their neighboring minima (as shown
in figure 3-2). Since the term
has a local minimum, particularly at the relatively deep minima,
which are significantly lower than their neighboring minima (as shown
in figure 3-2). Since the term
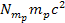 in equation 3-1-20 is independent of location (and time), it does not
have any effect on the location of the minima and can be removed.
The term
in equation 3-1-20 is independent of location (and time), it does not
have any effect on the location of the minima and can be removed.
The term
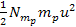 will cause the total energy minima to depart slightly from the
potential energy minima, and will shift the orbits of objects in the
outward direction, away from the potential energy minimum contours
(thus creating a force to balance the centrifugal force). Adhering
to the same logic used in equation 3-1-7, the Newtonian term
will cause the total energy minima to depart slightly from the
potential energy minima, and will shift the orbits of objects in the
outward direction, away from the potential energy minimum contours
(thus creating a force to balance the centrifugal force). Adhering
to the same logic used in equation 3-1-7, the Newtonian term
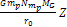 bears little influence on the location of the minima. Thus,
the high density concentrations should occur where bears little influence on the location of the minima. Thus,
the high density concentrations should occur where
Equation
3-1-21a
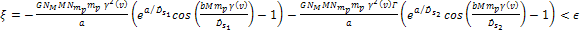
where
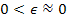 ,
and where ,
and where
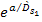 and
and
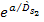 can
be replaced by 1, resulting in a non-negative
energy value for can
be replaced by 1, resulting in a non-negative
energy value for
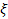 .
16 .
16
Equation
3-1-21b
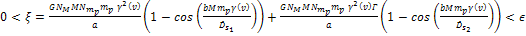
Equation
3-1-21b holds true in the immediate vicinity of the coordinates at
which both
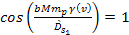 and
and
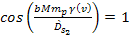 at the inertial frame
at the inertial frame
 ,
where ,
where
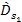 and
and
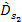 are given by equations 3-1-17a and 3-1-17b using
are given by equations 3-1-17a and 3-1-17b using
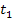 and
and
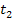 respectively. As expected, when applied to non-relativistic SHP
velocity
respectively. As expected, when applied to non-relativistic SHP
velocity
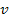 ,
the relativistic equation 3-1-21 provides identical results to the
non-relativistic equation 3-1-7, since at non-relativistic velocities ,
the relativistic equation 3-1-21 provides identical results to the
non-relativistic equation 3-1-7, since at non-relativistic velocities
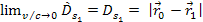 , ,
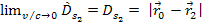 and
and . .
Section III-3: The
Creation and Motion of SHP groups
Current theories commonly attribute the creation of planets, stars
and galaxies to the gravitational collapse of clouds of gas.
According to UG Postulate IV, the extreme temperature and pressure
conditions that exist at the cores of large astronomical bodies
produce superheavy particles. As theorized here, the vast
amount of energy that is required for the creation of massive
superheavy particles is likely to originate from the energy released
by the collapse of ordinary matter towards the center of the
astronomical bodies, and by the high level of pressure and
temperature at their central core.17
By the time that an astronomical body reaches a steady state
condition, its center comprises of a dense core that contains a
significant portion of its ordinary matter, which rotates as a rigid
body with constant angular velocity
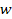 around its axis of rotation. The assumed circular orbits of the SHP
groups around the center of the astronomical body may or may not be
located within the central core. In either case, the interaction
between orbiting SHP groups and the core ordinary matter produces
rotating zones, with maxima and minima contours that intersect with
the volume of the core. When the angular velocity of any of the SHP
groups is equal to
around its axis of rotation. The assumed circular orbits of the SHP
groups around the center of the astronomical body may or may not be
located within the central core. In either case, the interaction
between orbiting SHP groups and the core ordinary matter produces
rotating zones, with maxima and minima contours that intersect with
the volume of the core. When the angular velocity of any of the SHP
groups is equal to
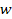 ,
these maxima and minima rotate in unison with the ordinary matter of
the central core, allowing both the core and the SHP groups to
maintain their angular velocity. Conversely, when the angular
velocity of any of the SHP groups orbiting the center of the
astronomical body varies from ,
these maxima and minima rotate in unison with the ordinary matter of
the central core, allowing both the core and the SHP groups to
maintain their angular velocity. Conversely, when the angular
velocity of any of the SHP groups orbiting the center of the
astronomical body varies from
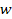 ,
the angular velocity of the resultant zonal pattern differs from the
angular velocity of the core ordinary matter. In such a scenario,
ordinary matter within the core will periodically either pass or be
overtaken by the maxima and minima of the rotating zone structure.
The forces that result from such encounters apply strong torques
which accelerate (or decelerate) the rotational velocity of the SHP
group, forcing it to converge to the angular velocity of the central
core. Therefore, a group composed of superheavy particles of mass ,
the angular velocity of the resultant zonal pattern differs from the
angular velocity of the core ordinary matter. In such a scenario,
ordinary matter within the core will periodically either pass or be
overtaken by the maxima and minima of the rotating zone structure.
The forces that result from such encounters apply strong torques
which accelerate (or decelerate) the rotational velocity of the SHP
group, forcing it to converge to the angular velocity of the central
core. Therefore, a group composed of superheavy particles of mass
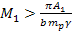 in a circular orbit of radius
in a circular orbit of radius
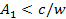 must rotate at the same angular velocity as the central core.18
Consequently, the speed of any SHP group
must rotate at the same angular velocity as the central core.18
Consequently, the speed of any SHP group
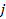 of SHP mass
of SHP mass
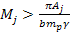 with an orbital radius of
with an orbital radius of
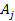 is given by 19
is given by 19
Equation
3-3-1
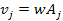
This
provides two very important rules that apply to superheavy particles
in circular orbit around the center of an astronomical body with a
massive rotating central core, where the zonal oscillation ranges of
these SHPs are longer than the radius of their orbit around the
center of the astronomical body:
Rule 1: In a steady state condition, all orbiting superheavy
particles fulfilling the above conditions share the same angular
momentum
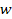 ,
where ,
where
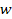 is the angular velocity of the central core of the astronomical body.
is the angular velocity of the central core of the astronomical body.
Rule 2: As a consequence of equation 3-3-1, and the requirement that
the velocity of a superheavy particle cannot surpass the speed of
light, the orbital radii of all superheavy particles that fulfill the
above conditions must be shorter than
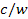 . .
There
are a few important questions regarding the nature and
characteristics of superheavy particles that must be addressed. What
is the mechanism that allows for and enables the generation of
superheavy particles? What mechanism forces superheavy particles
into nearly circular orbits around the center of the galaxy and
accelerates them to relativistic velocities? What prevents their
immediate annihilation or decay?
The process by which SHPs are created may be similar to the process
that generates a particle and an anti-particle of the same mass, such
as an electron and positron pair from photons. If that is the case,
the momentum and energy of the newly created SHP and anti-SHP are
determined by the energy and momentum of the high-energy photons from
which they originated. Newly created SHPs that do not have
sufficient kinetic energy to escape the (UG) gravitation of the
central core will enter an orbit around it. However, as the
superheavy particles settle into orbits, they are accelerated over a
relatively short period of time by the mechanisms described above,
and forced to move at an angular velocity equal to the angular
velocity
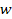 of the rotating central core. Therefore, according to equation
3-3-1, when the orbital radii of the SHPs are sufficiently large,
their velocities become relativistic. Note that complete stability
of a superheavy particle orbit can be achieved only if the orbit
becomes almost exactly circular (note that the orbit may become
slightly deformed by relativistic effects). A non-circular orbit
will create a wobbling effect of the zonal pattern relative to the
rotating ordinary particles within the planetís central core.
This wobbling effect will generate strong torques that force the SHP
into a circular orbit where its velocity is perpendicular to the
distance vector between the SHP location and the center of the core,
and where the angular velocity of the zonal maxima and minima that
cross the volume of the core is exactly the same as the angular
velocity of the core particles. Upon entering into orbit, the SHPís
velocity is still only a small fraction of its final speed when its
angular momentum becomes equal to
of the rotating central core. Therefore, according to equation
3-3-1, when the orbital radii of the SHPs are sufficiently large,
their velocities become relativistic. Note that complete stability
of a superheavy particle orbit can be achieved only if the orbit
becomes almost exactly circular (note that the orbit may become
slightly deformed by relativistic effects). A non-circular orbit
will create a wobbling effect of the zonal pattern relative to the
rotating ordinary particles within the planetís central core.
This wobbling effect will generate strong torques that force the SHP
into a circular orbit where its velocity is perpendicular to the
distance vector between the SHP location and the center of the core,
and where the angular velocity of the zonal maxima and minima that
cross the volume of the core is exactly the same as the angular
velocity of the core particles. Upon entering into orbit, the SHPís
velocity is still only a small fraction of its final speed when its
angular momentum becomes equal to
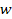 .
Consequently, when a superheavy particle enters an orbit with
relatively low velocity, other superheavy particles along the same
orbit with an angular velocity of .
Consequently, when a superheavy particle enters an orbit with
relatively low velocity, other superheavy particles along the same
orbit with an angular velocity of
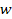 are moving at much higher speeds, and are therefore able to catch up
and bond20
with the new particle within a very short period of time, generating
a group of superheavy particles. This process may be repeated many
times as the SHP groups grow to include multiple superheavy
particles.
are moving at much higher speeds, and are therefore able to catch up
and bond20
with the new particle within a very short period of time, generating
a group of superheavy particles. This process may be repeated many
times as the SHP groups grow to include multiple superheavy
particles.
In
regard to the question of how superheavy particles remain stable,
avoiding either annihilation or decaying into smaller particles, all
known particles aside from protons and electrons (as well as their
anti-particles) are unstable when they are free or un-bonded.
However, the neutron, which is also unstable when free, is known to
become stable when it is bonded to a proton(s). The fact that SHPs
are bonded to the central core of the planet or to other SHPs (within
a group) may explain how they remain stable and avoid decay.
Moreover, the strong rejection zones between SHPs and anti-SHPs may
keep them apart and prevent their annihilation while in orbit around
the same center of rotation.
Section III-4: The
Issue of the Tail Wagging the Dog
At
first sight the UG theory seems to pose the inherent problem of the
ďtail wagging the dog.Ē As will be shown in the
following chapters, UG calculations suggest that SHP groups of a
total mass of the order of few hundreds of kilograms dictate the
overall structure of Saturnís ring and satellite system, which
amounts to an overall mass of approximately
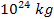 .
Similarly, SHP groups of a total mass of the order of .
Similarly, SHP groups of a total mass of the order of
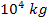 to
to
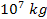 will be shown to determine the overall morphology of a galaxy of a
mass of about
will be shown to determine the overall morphology of a galaxy of a
mass of about
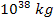 to
to
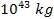 .
The force that a superheavy particle of a mass of .
The force that a superheavy particle of a mass of
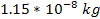 is capable of exerting on ordinary matter within its zonal
oscillation range at distances of
is capable of exerting on ordinary matter within its zonal
oscillation range at distances of
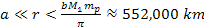 is about is about
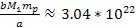 times larger than the Newtonian force applied by a point-like sphere
of ordinary matter of a total mass of
times larger than the Newtonian force applied by a point-like sphere
of ordinary matter of a total mass of
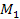 from the same distance. 21
from the same distance. 21
However, as the mass of the SHP groups is negligible in comparison
to the mass of ordinary matter within a galactic disk, or within a
system of planetary rings and satellites, the SHP orbits should be
profoundly affected by the gravitational influence of ordinary
matter. Furthermore, the overall SHP effect exerted on the heavier
ordinary matter should be minimal, as the overall mass of the
ordinary matter of a galactic or planetary system is larger by many
orders of magnitude. Yet, as will be seen, the model here assumes,
for example, that in the case of planetary systems, the orbits of
SHP groups are completely unaffected by the matter in the rings and
satellites, while the rings and the satellite orbits are curved by
the effect of the SHP groups.
The logic behind this assumption is quite simple. The SHP groups
are not free, and are held in circular orbit by the central rotating
core of the planet. As the superheavy particles transfer energy and
angular momentum to orbiting matter outside of the massive central
core, they may lose angular momentum and energy to the orbiting
objects, yet are prevented from slowing down or leaving their orbit
around the central core, which is few orders of magnitude heavier
than the overall mass of the planetís ring and satellite
system. Moreover, the same mechanism which led to equation 3-3-1 (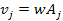 )
forces the SHPs to rotate around the center of the planet at the
exact same angular velocity )
forces the SHPs to rotate around the center of the planet at the
exact same angular velocity
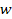 as the central core. In addition, the SHP group is prevented from
significantly reducing or increasing its radius of orbit by the
nearby maxima that confined its orbit. Therefore, the energy and
angular momentum lost (or gained) by the SHP to the ring and
satellite system must be replenished immediately by the far more
massive rotating central core. Consequently, the SHP group will
maintain the same angular velocity as that of the rotating center and
the same orbit and speed. An analogy to this concept is the image of
a free rigid rod of almost no mass pushing a small ship. As the mass
of the rod is negligible compared with the mass of the ship, the
force acting between the two objects will essentially influence the
momentum and velocity of the rod, bearing virtually no effect on the
momentum and velocity of the ship. However, if the rod is attached
to a much larger ship that is using the rod to push the small ship,
the opposite effect will occur, and there will be minimal change in
the momentum and speed of the rigid rod, which is now part of the
much larger ship, while the momentum and velocity of the small ship
will change significantly.
as the central core. In addition, the SHP group is prevented from
significantly reducing or increasing its radius of orbit by the
nearby maxima that confined its orbit. Therefore, the energy and
angular momentum lost (or gained) by the SHP to the ring and
satellite system must be replenished immediately by the far more
massive rotating central core. Consequently, the SHP group will
maintain the same angular velocity as that of the rotating center and
the same orbit and speed. An analogy to this concept is the image of
a free rigid rod of almost no mass pushing a small ship. As the mass
of the rod is negligible compared with the mass of the ship, the
force acting between the two objects will essentially influence the
momentum and velocity of the rod, bearing virtually no effect on the
momentum and velocity of the ship. However, if the rod is attached
to a much larger ship that is using the rod to push the small ship,
the opposite effect will occur, and there will be minimal change in
the momentum and speed of the rigid rod, which is now part of the
much larger ship, while the momentum and velocity of the small ship
will change significantly.
|



