Before proceeding further, it is important to address the oscillating
behavior of the UG potential energy demonstrated in figures 2-3 to
2-6.
Equation
2-1-1
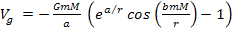
Whereas
the gravitational force described by Newton’s equation
increases monotonically with a reduction in the distance between a
pair of particles and is purely attractive, the UG potential equation
incorporates a cosine term. The cosine enables a cyclical function
to alternate between -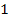 and
and
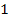 ,
and its inclusion in equation 2-1-1 implies that at short distances ,
and its inclusion in equation 2-1-1 implies that at short distances
 the UG equation alternates between zones of attraction and zones of
repulsion. The cosine term further implies that there are an infinite
number of distances at which the UG force or potential energy cross
zero, as well as an infinite number of distances at which they assume
local maxima or minima.
the UG equation alternates between zones of attraction and zones of
repulsion. The cosine term further implies that there are an infinite
number of distances at which the UG force or potential energy cross
zero, as well as an infinite number of distances at which they assume
local maxima or minima.
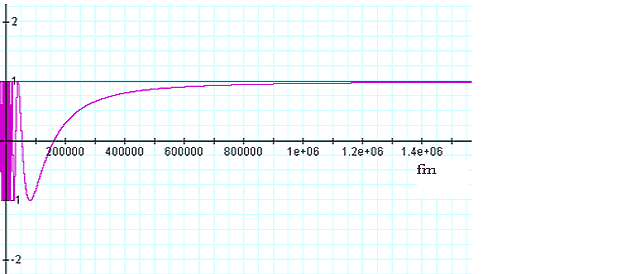
Figure 2-1 illustrates that the cyclical behavior of the UG equation
can be restricted to very short distances, well below the range of
distances where gravitation has been tested experimentally. The graph
uses an example of the general function
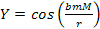 compared to unity. When
compared to unity. When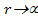 , ,
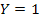 .
As the value of .
As the value of
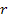 decreases,
decreases,
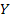 reduces monotonically, yet remains almost indistinguishable from 1
until a distance of about
reduces monotonically, yet remains almost indistinguishable from 1
until a distance of about
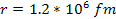 ,
which is slightly larger than the size of a typical atom or molecule.
As ,
which is slightly larger than the size of a typical atom or molecule.
As
 is further reduced,
is further reduced,
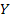 continues to drop monotonically until it becomes equal to zero at
continues to drop monotonically until it becomes equal to zero at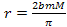 .
At .
At
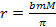 , ,
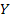 reaches its first minimum at
reaches its first minimum at
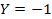 .
As .
As
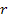 continues to decrease,
continues to decrease,
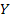 begins oscillating between
begins oscillating between
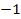 and
and
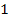 with growing frequency. Similarly, figure 2.2 compares the behavior
of
with growing frequency. Similarly, figure 2.2 compares the behavior
of
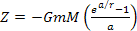 with the behavior of
with the behavior of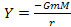 .
The two functions are indistinguishable from each other at distances
of .
The two functions are indistinguishable from each other at distances
of
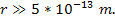 Therefore, using the set of numbers given in the previous example,
both terms,
Therefore, using the set of numbers given in the previous example,
both terms,
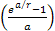 and
and
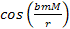 are, for all practical purposes, indistinguishable from
are, for all practical purposes, indistinguishable from
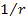 and
and
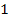 respectively at distances of
respectively at distances of
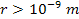 .1
In figures 2-3 to 2-6, the exponent and the cosine terms are
combined into the UG potential energy equation 2-1-1. Again, using
the same selected values and the given display scales, the UG
potential energy .1
In figures 2-3 to 2-6, the exponent and the cosine terms are
combined into the UG potential energy equation 2-1-1. Again, using
the same selected values and the given display scales, the UG
potential energy
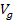 can hardly be distinguished from the Newtonian potential
can hardly be distinguished from the Newtonian potential
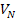 at distances of
at distances of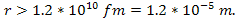 Under the assumption that the UG force is a conserving force, the UG
gravitational force
Under the assumption that the UG force is a conserving force, the UG
gravitational force
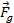 between two particles of respective mass
between two particles of respective mass
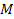 and
and
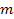 can be calculated by computing the gradient of
can be calculated by computing the gradient of
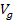 ,
given by equation 2-1-1. As the force is further assumed to be a
central force, equation 2-1-1 is dependent only on the distance ,
given by equation 2-1-1. As the force is further assumed to be a
central force, equation 2-1-1 is dependent only on the distance
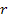 ,
and independent of any orientation angle.2
Therefore, only the radial derivative must be taken into account,
leading to ,
and independent of any orientation angle.2
Therefore, only the radial derivative must be taken into account,
leading to
Equation
2-1-2
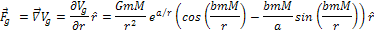
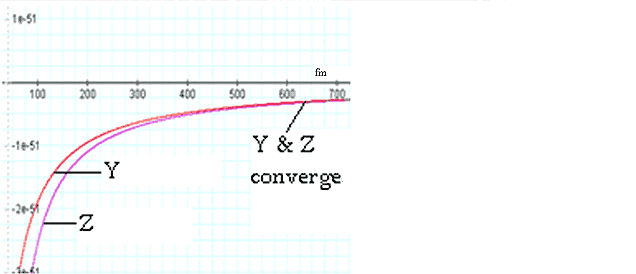
Figure
2-1: Comparison
between
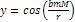 and
and
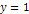 using
using
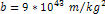 , ,
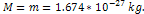 The x
axis provides the distance
The x
axis provides the distance
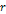 in
in
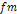 .
The two functions converge at about .
The two functions converge at about
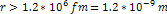 . .
Figure
2-2: Compares
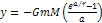 ,
denoted as ,
denoted as
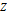 ,
to ,
to
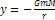 ,
denoted as Y, where ,
denoted as Y, where
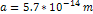 . .
In the general case
of two objects consisting of a variety of particles, where the first
object is composed of an ensemble of particles of particle mass
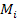 and the second object is composed of an ensemble of particles of
particle mass
and the second object is composed of an ensemble of particles of
particle mass
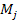 ,
the UG potential energy between the two objects ,
the UG potential energy between the two objects is given by
is given by
Equation
2-1-3
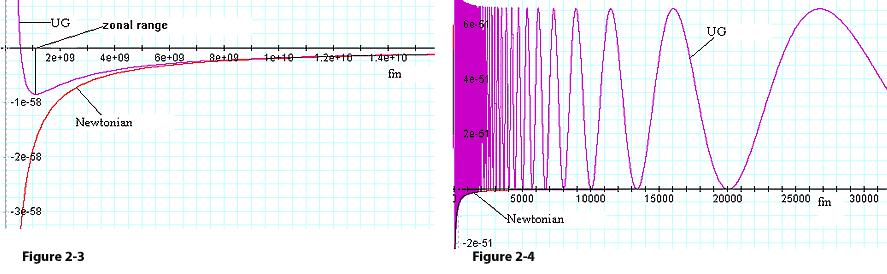
Figure
2-3: The UG and
Newtonian potential equations are compared in a display range of
 ,
using values of ,
using values of
 , ,
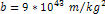 , ,
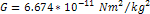 ,
and ,
and
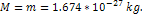 The two functions converge at about
The two functions converge at about
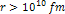 . .
Figure
2-4: Displays the
same comparison as figure 2.3, viewed in a display range of
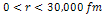 .
In this range, as long as .
In this range, as long as
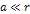 ,
the UG potential energy ,
the UG potential energy
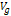 oscillates with a
large, almost constant amplitude (relative to the Newtonian
potential), and with increasing frequency as oscillates with a
large, almost constant amplitude (relative to the Newtonian
potential), and with increasing frequency as
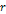 approaches zero. Note that
approaches zero. Note that
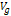 is essentially positive, and only briefly negative near its minima
that reside on the Newtonian curve.
is essentially positive, and only briefly negative near its minima
that reside on the Newtonian curve.
Figures
2-5 and 2-6:
Comparison between the UG and Newtonian potential equations, viewed
in display ranges of
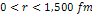 and
and
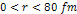 respectively. Note that at low
respectively. Note that at low
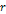 values (below about
values (below about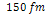 )
there is an explosive increase in amplitude, saturating the display
scale almost instantly. )
there is an explosive increase in amplitude, saturating the display
scale almost instantly.
The summations over
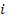 and
and
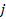 include all of the particles in objects 1 and 2 respectively, and
include all of the particles in objects 1 and 2 respectively, and
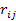 is the distance between the particle of mass
is the distance between the particle of mass
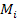 in the first object and the particle of mass
in the first object and the particle of mass
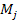 in the second object.
in the second object.
For simplicity, let it be assumed that the first object is composed
of
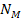 identical particles of particle mass
identical particles of particle mass
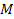 and the second object is composed of
and the second object is composed of
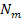 identical particles of particle mass
identical particles of particle mass
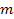 .
Furthermore, the distance .
Furthermore, the distance
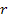 between the two objects is assumed to be substantially larger than
the size (or diameter) of either object. Consequently, the potential
energy equation is given by
between the two objects is assumed to be substantially larger than
the size (or diameter) of either object. Consequently, the potential
energy equation is given by
Equation 2-1-4
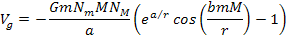
Similarly,
the unified gravitational force
 is provided by
is provided by
Equation
2-1-5
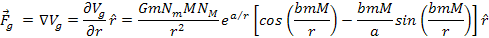
Therefore,
at distances , ,
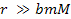 and
and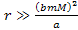 ,
where ,
where
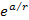 and
and
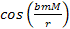 approach 1 and
approach 1 and
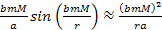 approaches zero, the UG force equation converges to
approaches zero, the UG force equation converges to
Equation
2-1-6
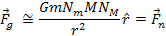
where
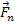 denotes the Newtonian force, thereby
denotes the Newtonian force, thereby demonstrating
that the UG and Newtonian forces converge at far distances.3
In general, at the limit demonstrating
that the UG and Newtonian forces converge at far distances.3
In general, at the limit
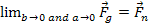 .
Thus, both theories provide the same results for any gravitational
system that is composed of ordinary particles, as long as the
constants .
Thus, both theories provide the same results for any gravitational
system that is composed of ordinary particles, as long as the
constants
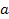 and
and
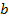 are sufficiently small, and the distance
are sufficiently small, and the distance
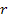 is not sub-microscopic.
is not sub-microscopic.
The underlying postulate that the unified gravitational force
equation can also be applied to the strong interaction suggests that
in the nucleus of an atom, where the distance between the nucleons is
about
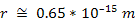 ,
the UG potential energy between two protons will be virtually equal
in amplitude to the Coulomb potential. Therefore,4
using equation 2-1-1 and Coulomb’s law, ,
the UG potential energy between two protons will be virtually equal
in amplitude to the Coulomb potential. Therefore,4
using equation 2-1-1 and Coulomb’s law,
Equation
2-1-7
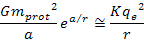
Multiplying by the
constant
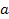 and taking the log of both sides provides
and taking the log of both sides provides
Equation
2-1-8
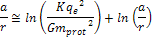
Substituting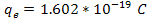 for the proton charge,
for the proton charge,
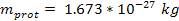 for the proton mass,
for the proton mass,
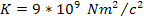 , ,
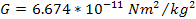 ,
and ,
and
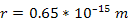 ,
and solving equation 2-1-8 via iterations provides the approximate
value of the constant ,
and solving equation 2-1-8 via iterations provides the approximate
value of the constant
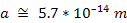 . .
Evaluating
the exponential values at distances of
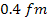 , ,
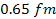 ,
and ,
and
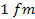 ,
with the assumption that ,
with the assumption that
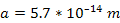 will increase the UG force by a factor of about
will increase the UG force by a factor of about
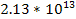 between 1
between 1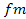 and
and
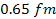 ,
and by a factor of about ,
and by a factor of about
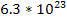 between
between
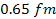 and
and
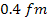 .
Therefore, equations 2-1-1 and 2-1-2 provide the necessary explosive
growth at approximately .
Therefore, equations 2-1-1 and 2-1-2 provide the necessary explosive
growth at approximately
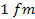 and below, while asymptotically converging to the Newtonian force for
ordinary particles at distances significantly larger than about
and below, while asymptotically converging to the Newtonian force for
ordinary particles at distances significantly larger than about
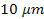 . .
Finding the value of the constant
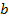 is more complicated, as the oscillations could have started at
distance ranges where the amplitude of the UG potential energy is
negligible compared with the electromagnetic potential energy, and
are thus difficult to detect.
is more complicated, as the oscillations could have started at
distance ranges where the amplitude of the UG potential energy is
negligible compared with the electromagnetic potential energy, and
are thus difficult to detect.
A
lower bound for the constant
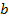 can be attained by taking into account the stability of the nucleus,
where the distances between the nucleons average about
can be attained by taking into account the stability of the nucleus,
where the distances between the nucleons average about
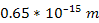 ,
requiring that a minimum occur at about this distance. For a minimum
to occur, the interaction between the nucleons at ,
requiring that a minimum occur at about this distance. For a minimum
to occur, the interaction between the nucleons at
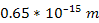 must be within the oscillation range of the cosine term, or
must be within the oscillation range of the cosine term, or
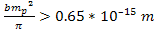 ,
leading to ,
leading to
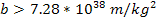 .5 .5
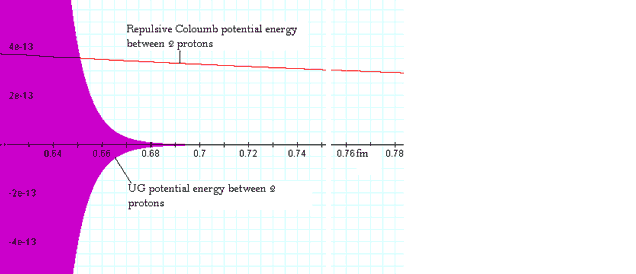
Figure
2-7: The graph
demonstrates the explosive growth of the UG potential energy at the
nuclear boundaries. As calculated in the case of two proton
interactions, the amplitude of the UG potential energy is equal in
magnitude to the Coulomb
potential energy at about
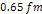 .
At distances below .
At distances below
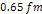 ,
the UG potential energy completely dominates over the electromagnetic
potential energy (with the exception of the UG zero crossings). At
just above ,
the UG potential energy completely dominates over the electromagnetic
potential energy (with the exception of the UG zero crossings). At
just above
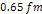 ,
however, the UG potential energy becomes negligible. ,
however, the UG potential energy becomes negligible.
The requirement that the UG force equation be consistent with the
Newtonian force equation within the level of measurement reliability
can be used for estimating an upper bound for the value of the
constant
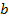 .
To date, all measurements of .
To date, all measurements of
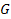 have been conducted at distances
have been conducted at distances
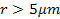 ,
where ,
where
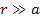 .
Therefore, the exponential term can be replaced by a value of .
Therefore, the exponential term can be replaced by a value of
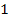 ,
leading to ,
leading to
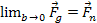 ,
assuring that the two forces are indistinguishable at the distance
range of interest when the value of ,
assuring that the two forces are indistinguishable at the distance
range of interest when the value of
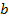 is sufficiently small. The variation in the measurement of the
gravitational constant (one part in
is sufficiently small. The variation in the measurement of the
gravitational constant (one part in
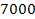 for
for
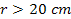 (Gillies, 1997)) can provide the upper bound of the
constant
(Gillies, 1997)) can provide the upper bound of the
constant
 by calculating the range of the acceptable deviation between the
forces calculated by the UG and the Newtonian equations. This level
of variation in
by calculating the range of the acceptable deviation between the
forces calculated by the UG and the Newtonian equations. This level
of variation in
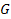 may be caused by the following:
may be caused by the following:
1. Measurement error- Since the gravitational force is
significantly weaker than the electromagnetic force, the
signal-to-noise ratio is low. In addition, as there is no negative
mass, the external gravitational fields cannot be masked out.
2. The presence of additional (relatively light) superheavy
particles that interact according to equations 2-1-1 and 2-1-2, but
do not dominate the interaction.
3. Variation between the gravitational force and Newton’s
equations when applied to ordinary matter.
The
failure to find an exact value of
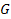 despite substantial improvements in measurement technology suggests
that measurement error alone cannot entirely account for the
deviation. As no stable SHP has ever been detected on the surface of
Earth, the second option seems unlikely. Therefore, the variability
of
despite substantial improvements in measurement technology suggests
that measurement error alone cannot entirely account for the
deviation. As no stable SHP has ever been detected on the surface of
Earth, the second option seems unlikely. Therefore, the variability
of
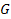 is presumably a consequence of the deviation of gravity from the
Newtonian equation. Finding the accurate value of
is presumably a consequence of the deviation of gravity from the
Newtonian equation. Finding the accurate value of
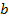 requires a detailed analysis that takes into account the geometry of
the specific experiment, as well as the fact that ordinary matter
molecules contain electrons, protons and neutrons of different
masses.
requires a detailed analysis that takes into account the geometry of
the specific experiment, as well as the fact that ordinary matter
molecules contain electrons, protons and neutrons of different
masses.
As
an example, assume that the experiment for measuring the
gravitational constant is conducted by measuring the force between
two identical homogeneous spheres of density
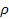 (in units of number of molecules per cubic meter) with radius
(in units of number of molecules per cubic meter) with radius
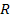 .
When measurements take place, the two centers of the spheres are .
When measurements take place, the two centers of the spheres are
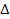 meters apart along the
meters apart along the
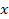 axis. Each molecule of the matter enclosed in the two spheres
contains
axis. Each molecule of the matter enclosed in the two spheres
contains
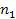 protons of mass
protons of mass
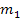 ,
an average of ,
an average of
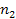 neutrons of mass
neutrons of mass
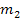 (the number of neutrons must be averaged from all stable isotopes),
and
(the number of neutrons must be averaged from all stable isotopes),
and
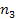 electrons of mass
electrons of mass
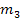 (due to molecular neutrality
(due to molecular neutrality
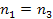 ). ).
According
to Newton’s law,
Equation
2-1-9a
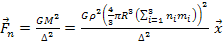
while
according to the UG theory,
Equation
2-1-9b
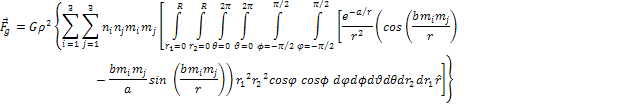
where
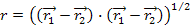 , ,
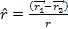 ,
and ,
and
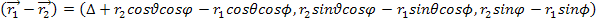 . .
The
terms
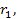
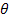 and
and
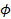 respectively provide the distance from the center, the azimuth and
the elevation angles of the volume point within the first sphere, and
respectively provide the distance from the center, the azimuth and
the elevation angles of the volume point within the first sphere, and
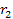 , ,
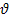 and
and
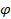 are their counterparts in the second sphere. As the two spheres are
not in contact,
are their counterparts in the second sphere. As the two spheres are
not in contact,
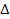 must be larger than
must be larger than
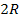 and all possible pairs of particles split between the two spheres
must be separated by a distance of at least
and all possible pairs of particles split between the two spheres
must be separated by a distance of at least
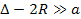 .
Therefore, the term .
Therefore, the term
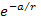 can
be replaced by can
be replaced by
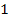 . .
Equation
2-1-9c
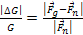
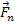 and
and
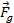 are given by equations 2-1-9a and 2-1-9b, and the calculated
are given by equations 2-1-9a and 2-1-9b, and the calculated
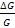 is consequently dependent on the value of the constant
is consequently dependent on the value of the constant
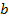 .
Therefore, the optimal value of .
Therefore, the optimal value of
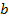 can then be estimated by finding the range of values that provide the
best fit between the calculated and measured
can then be estimated by finding the range of values that provide the
best fit between the calculated and measured
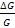 at different values of
at different values of
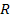 and
and
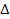 .
It is clear from the discussion above that .
It is clear from the discussion above that
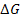 should approach zero as
should approach zero as
 approaches zero, as long as
approaches zero, as long as
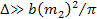 and
and
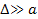 . .
In the absence of such an experiment, the value of
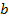 could be estimated from the reported range of variation of the value
of
could be estimated from the reported range of variation of the value
of
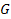 .
The gravitational contribution of an electron and the effect of the
small difference between the proton and neutron masses are relatively
small in comparison to the contribution of either a proton or a
neutron. Therefore, the contribution of the electrons to the
gravitational force is assumed to be negligible, while protons and
neutrons are assumed for simplicity to have an equal mass of .
The gravitational contribution of an electron and the effect of the
small difference between the proton and neutron masses are relatively
small in comparison to the contribution of either a proton or a
neutron. Therefore, the contribution of the electrons to the
gravitational force is assumed to be negligible, while protons and
neutrons are assumed for simplicity to have an equal mass of
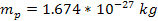 .
In addition, the distance .
In addition, the distance
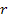 must be between
must be between
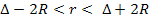 .
Using equations 2-1-9a, 2-1-9b and 2-1-9c for the case where .
Using equations 2-1-9a, 2-1-9b and 2-1-9c for the case where
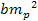 and
and
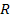 are significantly smaller, but not negligible compared with the
distance
are significantly smaller, but not negligible compared with the
distance
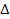 ,
provides ,
provides
Equation
2-1-9d
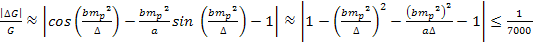
Given that
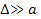 or or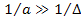 , ,
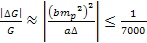 . .
Since the deviation
in
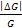 can reach the value of
can reach the value of
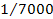 from time to time,
from time to time,
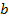 should be of the order of
should be of the order of
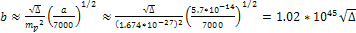 .
As typical high precision laboratory-based experiments were
conducted at distances of the order of .
As typical high precision laboratory-based experiments were
conducted at distances of the order of
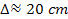 ,
the value of the constant ,
the value of the constant
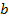 is likely to be in the general range of
is likely to be in the general range of
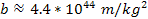 .
This estimated value is only an approximation, however, and may be
off by as much as one to two orders of magnitude. For the purpose of
discussion, as the exact values of the constants .
This estimated value is only an approximation, however, and may be
off by as much as one to two orders of magnitude. For the purpose of
discussion, as the exact values of the constants
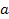 and
and
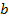 are not known, values of
are not known, values of
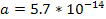 and
and
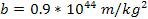 will be assumed for the remainder of this book. Furthermore, the
gravitational contribution of the electrons and the effect of the
small difference between proton and neutron masses will also be
assumed to be insignificant.6
Instead, a mass of
will be assumed for the remainder of this book. Furthermore, the
gravitational contribution of the electrons and the effect of the
small difference between proton and neutron masses will also be
assumed to be insignificant.6
Instead, a mass of
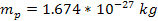 will be used for either a nucleon or the hydrogen atom
will be used for either a nucleon or the hydrogen atom
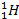 .
The term “ordinary particle” (or “ordinary
matter”) will be used throughout this book to refer to either a
proton, a neutron or an electron (or to matter composed of these
particles), while an ordinary particle of mass .
The term “ordinary particle” (or “ordinary
matter”) will be used throughout this book to refer to either a
proton, a neutron or an electron (or to matter composed of these
particles), while an ordinary particle of mass
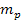 will refer specifically to either the hydrogen atom
will refer specifically to either the hydrogen atom
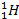 ,
a proton or a neutron. An object composed of ordinary matter that
contains one or more atoms or molecules with one or more nucleons
will be regarded as having ,
a proton or a neutron. An object composed of ordinary matter that
contains one or more atoms or molecules with one or more nucleons
will be regarded as having
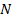 particles of mass
particles of mass
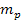 ,
where ,
where
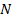 is the overall number of nucleons in the object. Finally, for the
remainder of this chapter, particle velocities will be assumed to be
non-relativistic.
is the overall number of nucleons in the object. Finally, for the
remainder of this chapter, particle velocities will be assumed to be
non-relativistic.
Section II-1: The
UG Gravitational Zones at Non-Relativistic Velocities
According to
equations 2-1-1 and 2-1-2, the UG interaction between a particle of
mass
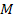 at
a given location and a second particle of mass at
a given location and a second particle of mass
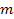 divides the space surrounding the first particle into zones that
define the force and potential energy acting on the second particle
by the first at any location within this space. The equations below
have been developed for the non-relativistic case to quantify the
widths and boundaries of the zones, and to find where they reach a
local maximum or minimum.
divides the space surrounding the first particle into zones that
define the force and potential energy acting on the second particle
by the first at any location within this space. The equations below
have been developed for the non-relativistic case to quantify the
widths and boundaries of the zones, and to find where they reach a
local maximum or minimum.
The local
potential energy maxima and minima (where the force is equal to zero)
are given by
Equation
2-1-10
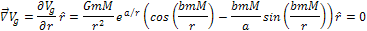
or
Equation
2-1-11
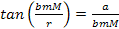
or
Equation
2-1-12
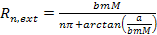 for
for
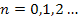
with minima at even
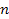 values and maxima at odd
values and maxima at odd
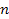 values. Similarly, applying equation 2-1-1 and the relation
values. Similarly, applying equation 2-1-1 and the relation
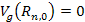 may provide the zero intersections
may provide the zero intersections
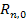 of the potential energy function
of the potential energy function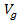 , ,
Equation
2-1-13
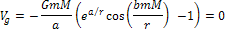
or
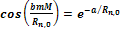 ,
thus ,
thus
Equation
2-1-14
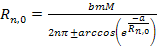
For distances
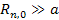 , ,
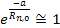 ,
and therefore7 ,
and therefore7
Equation
2-1-15
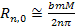 ,
for ,
for
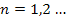
A
zone is defined as the area of space enclosed between a minimum curve
and an immediate neighboring maximum curve. Any zone
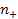 ,
refers to the zone situated between the minimum indexed ,
refers to the zone situated between the minimum indexed
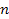 and the maximum indexed
and the maximum indexed
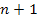 ,
while any zone ,
while any zone
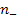 refers to the zone situated between the same minimum
refers to the zone situated between the same minimum
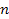 and the maximum curve indexed
and the maximum curve indexed
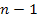 .
The distance between two successive maxima or two successive minima
can be found by using equation 2-1-12 for the usual case of .
The distance between two successive maxima or two successive minima
can be found by using equation 2-1-12 for the usual case of
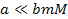 ,
or for the case of ,
or for the case of
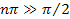 .
Since .
Since
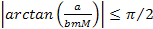 , ,
Equation
2-1-16
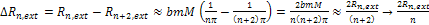 as
as
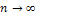
Similarly,
it can be shown that
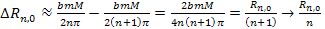 as
as
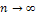 . .
Figures 2-3 to 2-6
illustrate the behavior of the function
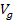 (using equation 2-1-1)compared with the Newtonian
gravitational potential at different distance ranges. As demonstrated
in figure 2-3, the two functions are virtually identical at distances
sufficiently greater than the first minimum (
(using equation 2-1-1)compared with the Newtonian
gravitational potential at different distance ranges. As demonstrated
in figure 2-3, the two functions are virtually identical at distances
sufficiently greater than the first minimum (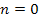 ),
which according to equation 2-1-12 occurs at ),
which according to equation 2-1-12 occurs at
Equation
2-1-17a

Below this point the
behaviors of the UG and the Newtonian functions diverge
substantially, as the UG potential Vg changes direction
and begins to exhibit an oscillation pattern with
 .
Initially, when .
Initially, when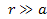 ,
the oscillation amplitude of the potential energy remains almost
constant at a value close to ,
the oscillation amplitude of the potential energy remains almost
constant at a value close to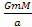 .
As .
As
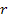 approaches or becomes smaller than the constant
approaches or becomes smaller than the constant
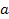 ,
both the amplitude and frequency of the oscillations increase sharply
with the reduction of distance ,
both the amplitude and frequency of the oscillations increase sharply
with the reduction of distance
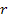 .
Since the oscillation frequency approaches infinity as .
Since the oscillation frequency approaches infinity as
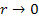 ,
the potential energy continues to alternate between rapidly growing
positive and negative potentials, which converge exponentially into
positive and negative infinities. An infinite amount of energy is
thus required to reduce the distance between the two particles to
zero. Therefore, the particles can never “meet,” and
singularity is avoided. If proven correct, this will have
a profound effect on the concept of black holes (black holes will be
discussed in section VII-2). ,
the potential energy continues to alternate between rapidly growing
positive and negative potentials, which converge exponentially into
positive and negative infinities. An infinite amount of energy is
thus required to reduce the distance between the two particles to
zero. Therefore, the particles can never “meet,” and
singularity is avoided. If proven correct, this will have
a profound effect on the concept of black holes (black holes will be
discussed in section VII-2).
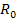 ,
defined above as the distance of the first minimum, serves as an
indicator for howclose the two particles must be from
each another before their gravitational interaction begins to deviate
strongly from the classical Newtonian behavior and proceeds into a
pattern of sinusoidal zones. For its significance, the distance ,
defined above as the distance of the first minimum, serves as an
indicator for howclose the two particles must be from
each another before their gravitational interaction begins to deviate
strongly from the classical Newtonian behavior and proceeds into a
pattern of sinusoidal zones. For its significance, the distance
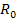 will be referred to as the zonal rangeof
the particles. In the case of two objects consisting of many types of
particles, the zonal rangebetweenthe heaviest
particle in each object will be defined as the maximal zonal
rangeof the objects. For example, in the
comparison between
will be referred to as the zonal rangeof
the particles. In the case of two objects consisting of many types of
particles, the zonal rangebetweenthe heaviest
particle in each object will be defined as the maximal zonal
rangeof the objects. For example, in the
comparison between
 and and
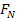 in
figure 2-8, we can observe that sufficiently far beyond the zonal
range distance in
figure 2-8, we can observe that sufficiently far beyond the zonal
range distance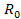 ,
the UGand the Newtonian forces are indistinguishable. In
other words, starting at somewhat beyond their zonal range ,
the UGand the Newtonian forces are indistinguishable. In
other words, starting at somewhat beyond their zonal range
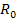 ,
the force between a pair of superheavy particles of mass ,
the force between a pair of superheavy particles of mass
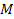 and
and
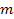 is equivalent to the force between two objects that are positioned at
the same distance
is equivalent to the force between two objects that are positioned at
the same distance
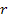 from each other, where the first object is composed of
from each other, where the first object is composed of
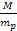 ordinaryparticles and the second object consists of
ordinaryparticles and the second object consists of
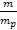 ordinary particles. This, however, is not the case for distances
within the particles’ zonal range. For larger
superheavy particles of mass
ordinary particles. This, however, is not the case for distances
within the particles’ zonal range. For larger
superheavy particles of mass
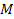 ,
which will be shown to be capable of generating planetary rings, ,
which will be shown to be capable of generating planetary rings,
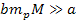 .
The SHP zonal range with
ordinary particles .
The SHP zonal range with
ordinary particles
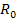 is given by equation 2-1-17a and is inversly proportional to
is given by equation 2-1-17a and is inversly proportional to
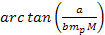 .
In cases where .
In cases where
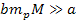 , ,
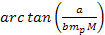 is very small, and the SHP zonal range
is very small, and the SHP zonal range
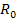 is located at an extremely large distance from the central core
of the planet (see equation 2-1-17a), significantly beyond the
distance where the UG potential energy oscillations cease. The
amplitude at this zonal minimum is also negligible. For this reason,
a second important distance, termed the zonal
oscillation rangeisdefined
as the radius of the first maximum (
is located at an extremely large distance from the central core
of the planet (see equation 2-1-17a), significantly beyond the
distance where the UG potential energy oscillations cease. The
amplitude at this zonal minimum is also negligible. For this reason,
a second important distance, termed the zonal
oscillation rangeisdefined
as the radius of the first maximum (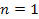 )
given by )
given by
Equation
2-1-17b
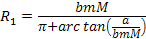
where the
potential energy becomes virtually
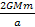 . .
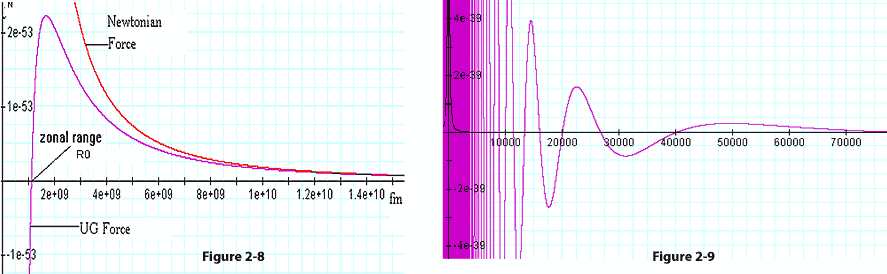
Figures
2-8 and 2-9: A
comparison between the UG force and the Newtonian gravitational
force, given the same
parameters used in figures 2-3 to 2-6. The two functions converge at
about
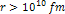 (
( ). ).
Section II-2: Superheavy Particles
Embedded in Ordinary Matter
According to the UG equation, a single massive superheavy particle
embedded in a large amount of ordinary matter can completely dominate
a significant amount of the surrounding region, yet remain completely
undetected at very long or short-range distances. In order to
demonstrate this concept, consider the following example of a
hypothetical object composed of
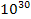 ordinary particles of particle mass
ordinary particles of particle mass
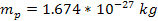 arranged in spherically symmetric distribution within a distance
arranged in spherically symmetric distribution within a distance
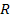 of a single superheavy particle of mass
of a single superheavy particle of mass
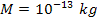 .
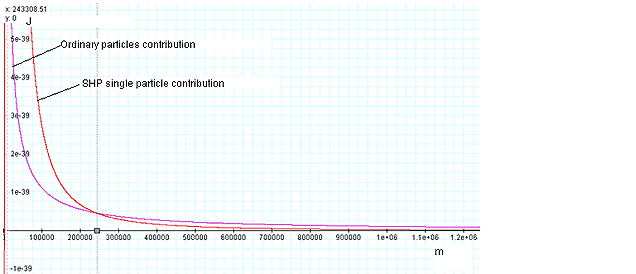
Figures 2-10 and 2-11 provide the comparison between the absolute
value of the contribution of the .
Figures 2-10 and 2-11 provide the comparison between the absolute
value of the contribution of the
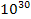 ordinary particles and the contribution of the single SHP of mass
ordinary particles and the contribution of the single SHP of mass
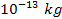 to the potential energy of a given ordinary particle at a distance
to the potential energy of a given ordinary particle at a distance
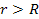 .
At distances significantly greater than the SHP zonal range with
ordinary matter, where the UG equation and the Newtonian equations
converge, the overall larger mass of the ordinary matter dominates
the interaction, and the SHP effect is completely negligible (smaller
by a factor of .
At distances significantly greater than the SHP zonal range with
ordinary matter, where the UG equation and the Newtonian equations
converge, the overall larger mass of the ordinary matter dominates
the interaction, and the SHP effect is completely negligible (smaller
by a factor of
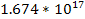 ).
As ).
As
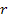 reduces to below about
reduces to below about
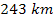 ,
the superheavy particle contribution begins to dominate. The SHP
dominance peaks at the ,
the superheavy particle contribution begins to dominate. The SHP
dominance peaks at the
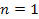 maximum, where its contribution becomes about 18.7 times larger than
the contribution of ordinary particles. As
maximum, where its contribution becomes about 18.7 times larger than
the contribution of ordinary particles. As
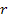 reduces below
reduces below
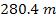 ,
the ratio ,
the ratio
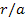 falls to a level at which the SHP effect is diminished by the
excessive mass of ordinary particles, and the ordinary matter
contribution once again becomes dominant. As
falls to a level at which the SHP effect is diminished by the
excessive mass of ordinary particles, and the ordinary matter
contribution once again becomes dominant. As
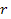 continues
to drop, the contribution of the superheavy particle becomes
completely negligible, as long as continues
to drop, the contribution of the superheavy particle becomes
completely negligible, as long as
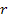 remains greater than
remains greater than
 . .
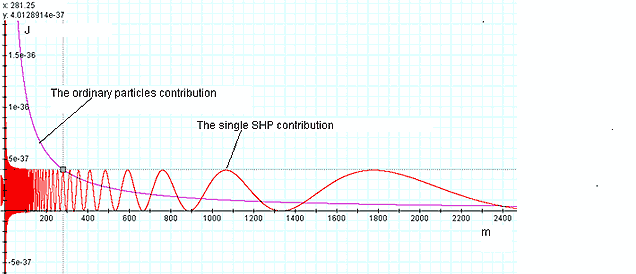
Figure
2-10: A comparison
between the inverted contribution of
 ordinary particles and the contribution of a single SHP
of mass
ordinary particles and the contribution of a single SHP
of mass
 to the potential energy of an ordinary particle at distance
to the potential energy of an ordinary particle at distance
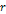 (
(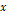 axis).
The ordinary particles clearly dominate at distances axis).
The ordinary particles clearly dominate at distances
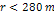 ,
while the SHPs begin to dominate at ,
while the SHPs begin to dominate at
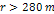 . .
Figure
2-11: Using the same
parameters as figure
2-10,the
SHP dominance is
terminated at
 ,
as ordinary matter begins to dominate the interaction at larger
distances. ,
as ordinary matter begins to dominate the interaction at larger
distances.
Between those extreme circumstances, however, there is a third
condition of a “nearly Newtonian environment.” This
environmental classification is comprised of ordinary matter and
superheavy particles, where the distances between objects are
adequately large that the SHP effect is detectable, but can be
treated as a small perturbation to the Newtonian equations (an
example of this is the formation of planetary rings, discussed in
Chapter V). A relatively simple way to estimate whether a
cosmological system is a “nearly Newtonian environment”
is to verify that the orbital motions of its bodies are in accordance
with Kepler’s laws of motion. The interactions between the
Sun, planets, and other objects in our Solar System, for instance,
are included in the “nearly Newtonian” class. However,
in the case of galaxies, or deep inside stars, planets or large
satellites, the environment can depart significantly from being
“nearly Newtonian.”
The UG interaction between two objects can be broken down to the sum
of two distinct groups according to the following equation:
Equation
2-1-18
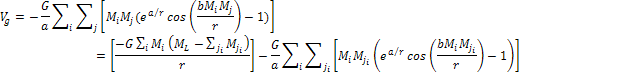
where
the first summation of index
 includes all of the particles in the first object, where the
summation of index
includes all of the particles in the first object, where the
summation of index
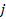 includes all of the particles in the second object, and where the
summation on
includes all of the particles in the second object, and where the
summation on
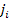 includes only the object 2 particles of mass
includes only the object 2 particles of mass
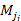 that are within ten times of their oscillation zonal range with the
particle
that are within ten times of their oscillation zonal range with the
particle
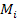 (and therefore, does not include particles of the second object which
comply with
(and therefore, does not include particles of the second object which
comply with
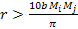 or
or
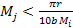 ).8
Combined with the requirement that
).8
Combined with the requirement that
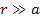 ,
the contributions to the UG potential energy of all pairs of
particles ,
the contributions to the UG potential energy of all pairs of
particles
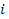 of
object 1 and particles of
object 1 and particles
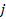 of object 2 that are not in the
of object 2 that are not in the
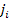 sub-group are reduced to approximately their Newtonian interactions.
As the overall mass of this group is equal to
sub-group are reduced to approximately their Newtonian interactions.
As the overall mass of this group is equal to
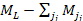 ,
where ,
where
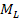 represents the total mass of the larger object 2, their overall
contribution can be replaced by the first term of equation 2-1-18.
While the first term describes a classical Newtonian gravitational
potential, the second term includes the interactions of all pairs for
which their calculated UG contribution to the potential energy of the
first object departs significantly from their calculated Newtonian
contribution. A similar approach can be taken to calculate the UG
force, where
represents the total mass of the larger object 2, their overall
contribution can be replaced by the first term of equation 2-1-18.
While the first term describes a classical Newtonian gravitational
potential, the second term includes the interactions of all pairs for
which their calculated UG contribution to the potential energy of the
first object departs significantly from their calculated Newtonian
contribution. A similar approach can be taken to calculate the UG
force, where
Equation 2-1-19
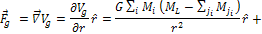
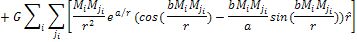
In the present case, both conditions of
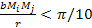 and
and
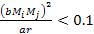 (or
(or
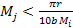 and
and
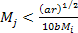 )
are required in order for the particle )
are required in order for the particle
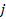 of object 2 to be in the first term of equation 2-1-19. The main
benefit of distinguishing between the two terms is that the linear
Newtonian term is in compliance with important Newtonian properties,
specifically Newton’s shell theorem, which states the
following:
of object 2 to be in the first term of equation 2-1-19. The main
benefit of distinguishing between the two terms is that the linear
Newtonian term is in compliance with important Newtonian properties,
specifically Newton’s shell theorem, which states the
following:
1. A spherically symmetric body affects external objects
gravitationally as though all of its mass were concentrated at its
center point.
2. An object inside a spherically symmetric shell feels no
gravitational force exerted by the shell, regardless of the object’s
location within the shell.
3. Within a solid sphere of constant density, the gravitational
force varies linearly with distance from the center, becoming zero at
the center of the mass.
While the shell theorem holds true when applied to the first term
(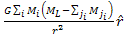 ),
the shell theorem does not hold true for the general UG force, and
therefore does not hold true for the second terms of equations 2-1-18
and 2-1-19. In summary, when the second terms of equations 2-1-18
and 2-1-19 are small relative to the first Newtonian terms, but still
detectable, the gravitational interaction between the two objects can
be classified as “nearly Newtonian”9 ),
the shell theorem does not hold true for the general UG force, and
therefore does not hold true for the second terms of equations 2-1-18
and 2-1-19. In summary, when the second terms of equations 2-1-18
and 2-1-19 are small relative to the first Newtonian terms, but still
detectable, the gravitational interaction between the two objects can
be classified as “nearly Newtonian”9
Although equation 2- 1-12 provides the minima
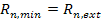 (for even
(for even
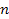 )
of the )
of the
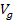 potential energy, the smaller object can become trapped
exactly at a minimum only if its velocity potential energy, the smaller object can become trapped
exactly at a minimum only if its velocity
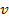 is equal to zero. In the more general case, where the small object
velocity is not zero, the orbit will deviate slightly outward from
the calculated circular radii of the potential
is equal to zero. In the more general case, where the small object
velocity is not zero, the orbit will deviate slightly outward from
the calculated circular radii of the potential
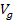 minima. For example, consider the gravitational interaction between
a large, spherically symmetric object of mass
minima. For example, consider the gravitational interaction between
a large, spherically symmetric object of mass
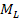 ,
and a significantly smaller spherically symmetric object of mass ,
and a significantly smaller spherically symmetric object of mass
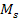 traveling in circular orbit around the large object at
non-relativistic velocity. The larger object is assumed to consist of traveling in circular orbit around the large object at
non-relativistic velocity. The larger object is assumed to consist of
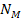 identical superheavy particles of mass
identical superheavy particles of mass
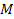 residing in a relatively small core at the center of the object, and
of ordinary particles of particle mass
residing in a relatively small core at the center of the object, and
of ordinary particles of particle mass
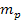 and
an overall total ordinary particle mass of and
an overall total ordinary particle mass of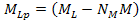 distributed throughout the object in a spherically symmetric form.
Similarly, the small orbiting object is assumed to consist of
distributed throughout the object in a spherically symmetric form.
Similarly, the small orbiting object is assumed to consist of
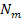 identical particles of particle mass
identical particles of particle mass
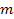 and a total mass of
and a total mass of
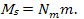 The
circular orbital radius The
circular orbital radius
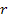 is assumed to be much greater than the sum of the radius of the small
object, the radius of the large object, and the zonal range between
the particles of masses
is assumed to be much greater than the sum of the radius of the small
object, the radius of the large object, and the zonal range between
the particles of masses
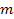 and
and
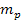 .
Since the orbit is assumed to be circular,10 .
Since the orbit is assumed to be circular,10
Equation
2-1-20
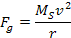
Therefore,
the kinetic energy
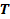 of the small object is given by
of the small object is given by
Equation
2-1-21
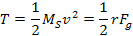
and
the overall sum of the small object potential and kinetic energies is
provided by
Equation
2-1-22
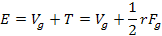
Substituting the
number of particles in each object and their respective masses into
equations 2-1-18 and 2-1-19 yields
Equation
2-1-23
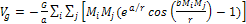
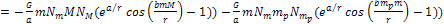
Since
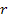 is assumed to be much larger than both
is assumed to be much larger than both
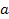 and the zonal range between particles of mass
and the zonal range between particles of mass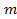 and
and
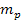 (therefore
(therefore
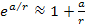 and
and
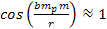 ),
and since both objects are assumed to contain a spherically symmetric
distribution of matter, ),
and since both objects are assumed to contain a spherically symmetric
distribution of matter,
Equation
2-1-24
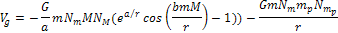
or using
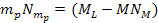 , ,
Equation
2-1-25
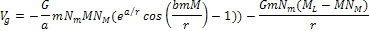
Similarly, the force
can be derived from equation 2-1-19, leading to
Equation
2-1-26
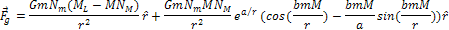
Substituting
equations 2-1-25 and 2-2-26 into equation 2-1-22,
Equation
2-1-27

leading to
Equation
2-1-28
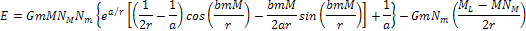
Thus,
Equation
2-1-29
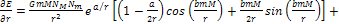
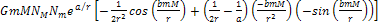 + +
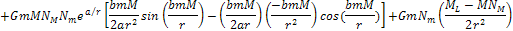
=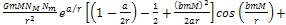
+
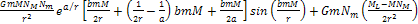
 = =
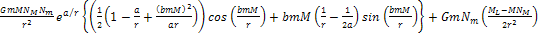
If the large object
does not consist of any ordinary particles (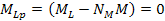 ),
the orbit will comply with the following equation: ),
the orbit will comply with the following equation:
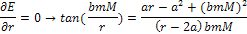
or
Equation
2-1-30
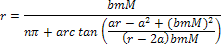
To calculate the
closest maximum or minimum in the vicinity of
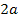 , ,
Equation
2-1-31
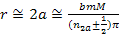
In cases where
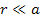 , ,
Equation
2-1-32
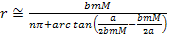
When
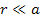 and
and
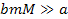 , ,
Equation
2-1-33
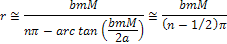
When
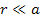 and
and
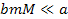 , ,
Equation
2-1-34
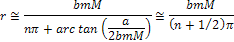
In cases where
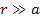 , ,
Equation
2-1-35
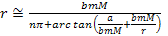
When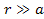 and
and
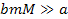 , ,
Equation
2-1-36
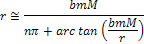
When
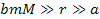 , ,
Equation
2-1-37
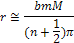
However, in most
cases the overall mass of ordinary matter is expected to exceed the
total SHP mass, or
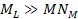 .
At distances far greater than the size of an atom nucleus, .
At distances far greater than the size of an atom nucleus,
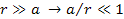 ,
and ,
and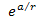 can be replaced by
can be replaced by
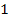 .
Therefore, equation 2-1-29 will become .
Therefore, equation 2-1-29 will become
Equation
2-1-38
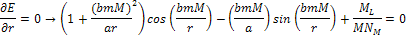
For
the usual case of
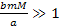 and
and
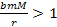 (where the orbiting object is within the zonal oscillation range),
this equation reduces to
(where the orbiting object is within the zonal oscillation range),
this equation reduces to
Equation
2-1-39
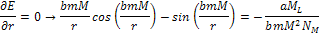
The
case of
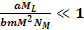 : :
In
the case of
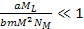 equation 2-1-39 leads to
equation 2-1-39 leads to
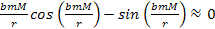 or to the same conclusion as in equation 2-1-36
or to the same conclusion as in equation 2-1-36
Equation
2-1-40
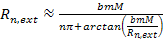 where
where
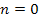 , ,
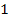 , ,
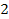 … …
with minima at even
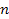 values and maxima at odd
values and maxima at odd
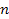 values. Thus minima occur at
values. Thus minima occur at
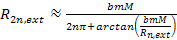 ,
where ,
where
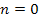 , ,
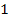 , ,
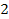 … …
The case of
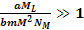 : :
In the case of
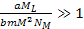 ,
the ,
the
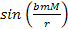 term in equation 2-1-39 is negligible (as
term in equation 2-1-39 is negligible (as
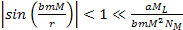 , thus
, thus
Equation
2-1-41
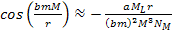
Consequently,
minima and maxima occur at
Equation
2-1-42
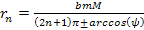
where
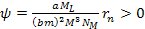 and
and
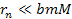 or
or
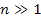 ,
and where minima occur at the ,
and where minima occur at the
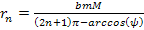 . .
Equation 2-1-41 can be solved only if
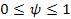 .
Therefore, for minima (and maxima) to occur, the distance .
Therefore, for minima (and maxima) to occur, the distance
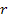 must comply with
must comply with
Equation
2-1-43
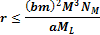
Note
that since
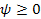 ,
the arccosine term is limited to the range ,
the arccosine term is limited to the range
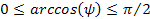 and
and
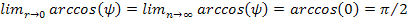 .
Additionally, equation 2-1-41 becomes accurate only where .
Additionally, equation 2-1-41 becomes accurate only where
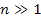 .
As .
As
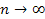 , ,
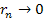 Therefore, for all practical purposes, if the condition of equation
2-1-42 is fulfilled, the minima are expected to occur at
Therefore, for all practical purposes, if the condition of equation
2-1-42 is fulfilled, the minima are expected to occur at
Equation
2-1-44
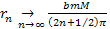
As a
reminder, the given scenario assumes that
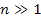 , ,
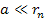
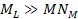 , ,
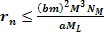 ,
and that ,
and that
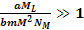 . .
The
case of
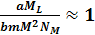
In
cases of
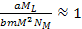 ,
equation 2-1-39 leads to ,
equation 2-1-39 leads to
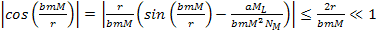 .
Therefore, .
Therefore,
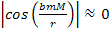 ,
and consequently, for an integer ,
and consequently, for an integer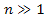 , ,
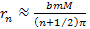 ,
where minima occur at approximately ,
where minima occur at approximately
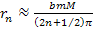 . .
|



