The Unification of
the Strong Interaction and the Gravitational Force
The theory of unified gravitation is based on the assumption that the
nuclear strong interaction and gravitation are one and the same
force, viewed at different distance scales, and that a single
equation can describe both interactions on nuclear as well as on
cosmological scales. In particular, it is assumed that similar to
Newton’s theory of gravitation, the unified gravitational
force is predominantly a central and conserving force between a pair
of particles. At large distances, the UG force equation should
asymptotically approach Newton’s classical force equation, when
applied to ordinary matter composed of protons, neutrons and
electrons, and should fully comply with all experimental measurements
of gravitation that are currently available. In addition, the UG
force must comply with the behavior of the nuclear forces between
nucleons, which have been observed to be substantially stronger than
the Coulomb interaction at below sub-Fermi distances. Accordingly,
the UG force must produce an explosive growth at distances below
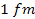 ,1
and is thus assumed to demonstrate exponential behavior. At a
microscopic distance range of approximately ,1
and is thus assumed to demonstrate exponential behavior. At a
microscopic distance range of approximately
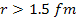 ,
the UG force between two protons must be negligible in comparison to
the Coulomb force. It is further assumed that the force is
independent of velocity and spin, as their effects are either
relatively small, or are part of the electromagnetic forces.
However, it should be noted that as energy and force equations are
not invariant under the Lorenz transformations, the force may not be
central and may become dependent on particle velocity when the
particles move at relativistic velocities. The UG theory must also be
capable of explaining the observed nuclear resonance patterns, as
well as planetary (and galactic) ring patterns, which consist of
thousands of ringlets (oscillation patterns). The large area occupied
by planetary and galactic rings rules out quantum mechanics as the
cause of the oscillations, thus indicating that the UG potential must
be driven by a periodic function. As most gravitational systems do
not demonstrate cyclical behavior, the oscillating term must be
suppressed under ordinary conditions. ,
the UG force between two protons must be negligible in comparison to
the Coulomb force. It is further assumed that the force is
independent of velocity and spin, as their effects are either
relatively small, or are part of the electromagnetic forces.
However, it should be noted that as energy and force equations are
not invariant under the Lorenz transformations, the force may not be
central and may become dependent on particle velocity when the
particles move at relativistic velocities. The UG theory must also be
capable of explaining the observed nuclear resonance patterns, as
well as planetary (and galactic) ring patterns, which consist of
thousands of ringlets (oscillation patterns). The large area occupied
by planetary and galactic rings rules out quantum mechanics as the
cause of the oscillations, thus indicating that the UG potential must
be driven by a periodic function. As most gravitational systems do
not demonstrate cyclical behavior, the oscillating term must be
suppressed under ordinary conditions.
Newton never published the reasoning that guided him to his
gravitational force equation and never attempted to prove the
equation on a theoretical basis. This is quite understandable, given
that fundamental principles cannot be proven to be correct and may be
regarded as valid only as long as they are not rendered false by
experimental results. The basic UG equation 1-7 has the same
limitation and cannot be proven correct. The equation will simply be
required to survive a continuous inflow of experimental data that may
either confirm or refute its accuracy. In the case that it is proven
to be incorrect, the equation should either be adjusted or its
theoretical foundation discarded. The logic underlying equation 1-7
is laid out in the following section of this chapter, where it will
be shown that mathematically a family of very similar equations may
be compatible with the aforementioned requirements. Equation 1-7 has
been selected as virtually the simplest equation fulfilling the
criteria.
Section I-1: The
Logic leading to the Theory of Unified Gravitation
The UG theory for the strong interaction and gravitation is based on
four postulates leading to a family of possible gravitational
equations. While the different possible equations may provide
different potential energy values, they share major properties that
can be shown to provide a simpler and more accurate theory than the
one currently used, with the ability to explain a large number of
unexplained observed phenomena. The first UG postulate states,
UG Postulate I: The nuclear strong interaction and
gravitation are actually one and the same interaction, viewed
on different distance scales. Therefore, a single equation can
describe both interactions from the sub-nuclear scale to the
cosmological scale.
Newton’s
gravitational equations 1-1 and 1-2 describe a central and conserving
force between a pair of particles. The force depends on the distance
between the two particles and on the product of their masses.
Therefore, a natural starting point for the UG theory is to assume
that the UG force is also a central and conserving force between a
pair of particles, and that the force depends exclusively on the
distance between the particles and on their respective masses. The
short-range strong force was also shown to depend on inter particle
distances and on particle masses, and to be dominated by central
forces. However, the strong force has also been shown to contain a
non-central component, and furthermore to depend relatively weakly on
the charge and spin of the particles. Thus, the assumption of a
central force that is entirely dependent on particle mass and
distance can be challenged for distances of the order of
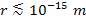 .
The weak dependency of the overall nuclear force on particle charge
and spin can be attributed to electromagnetic interactions between
the charged particles, or between their charges and the magnetic
fields generated by their motion and spin. The existence of a
non-central component can be attributed to a relativistic effect
caused by high particle velocities. Whereas two charges at rest
exert a central Coulomb force on each other, two relativistic charges
are known to exert a non-central magnetic force on each other, in
addition to the central Coulomb force. This phenomenon was explained
by Einstein to be a simple relativistic effect. The underlying cause
for this effect is that a force, under special relativity, is not an
invariant entity. In other words, due to the relativistic phenomena
of distance contraction and time dilation, force equations are not
the same when viewed in different inertial frames that move at
relativistic velocities relative to each other. Consequently, a
central force between two particles at rest would not be viewed as a
central force when both particles are moving at relativistic speeds
relative to the observer. These relativistic effects provide a
mechanism by which the central Coulomb force, as well as any other
central force between two particles at rest, can create a substantial
non-central force component (for further discussion see Chapter III).
Therefore, the existence of a strong central UG force and an
electromagnetic force between two massive charged particles can be
consistent with observations of non-central components, with some
weaker dependencies on the charge and spin of the interacting
particles. This enables the UG assumption that when viewed from an
inertial rest frame of one of the interacting particles, the unified
gravitational force is predominantly a central and conserving force
between a pair of particles, depending exclusively on the absolute
value of the distance between the particles and on their respective
masses, where the distance and masses are measured relative to the
given inertial rest frame. In cases where the test particle has a
relativistic velocity relative to the source particle, its perceived
mass and distance are altered by the relativistic effect. For the
time being, the discussion is limited to the non-relativistic case,
where the particle velocities, relative to each other and relative to
the observer, are significantly lower than the speed of light. The
discussion will be broadened in the third chapter of this book to
deal with relativistic particles as well. .
The weak dependency of the overall nuclear force on particle charge
and spin can be attributed to electromagnetic interactions between
the charged particles, or between their charges and the magnetic
fields generated by their motion and spin. The existence of a
non-central component can be attributed to a relativistic effect
caused by high particle velocities. Whereas two charges at rest
exert a central Coulomb force on each other, two relativistic charges
are known to exert a non-central magnetic force on each other, in
addition to the central Coulomb force. This phenomenon was explained
by Einstein to be a simple relativistic effect. The underlying cause
for this effect is that a force, under special relativity, is not an
invariant entity. In other words, due to the relativistic phenomena
of distance contraction and time dilation, force equations are not
the same when viewed in different inertial frames that move at
relativistic velocities relative to each other. Consequently, a
central force between two particles at rest would not be viewed as a
central force when both particles are moving at relativistic speeds
relative to the observer. These relativistic effects provide a
mechanism by which the central Coulomb force, as well as any other
central force between two particles at rest, can create a substantial
non-central force component (for further discussion see Chapter III).
Therefore, the existence of a strong central UG force and an
electromagnetic force between two massive charged particles can be
consistent with observations of non-central components, with some
weaker dependencies on the charge and spin of the interacting
particles. This enables the UG assumption that when viewed from an
inertial rest frame of one of the interacting particles, the unified
gravitational force is predominantly a central and conserving force
between a pair of particles, depending exclusively on the absolute
value of the distance between the particles and on their respective
masses, where the distance and masses are measured relative to the
given inertial rest frame. In cases where the test particle has a
relativistic velocity relative to the source particle, its perceived
mass and distance are altered by the relativistic effect. For the
time being, the discussion is limited to the non-relativistic case,
where the particle velocities, relative to each other and relative to
the observer, are significantly lower than the speed of light. The
discussion will be broadened in the third chapter of this book to
deal with relativistic particles as well.
As the UG force is assumed to be a central and conserving force, it
can be written as a gradient of a potential energy scalar function
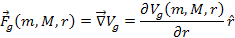
where
the distance vector between the two particles is given by
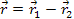 ,
where ,
where
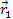 and
and
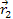 are the locations of the interacting particles and where
are the locations of the interacting particles and where
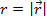 ,
and ,
and
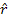 is defined as the unit vector in the direction of
is defined as the unit vector in the direction of
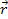 .
The respective rest masses of the particles are denoted .
The respective rest masses of the particles are denoted
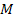 and
and
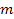 ,
the potential energy function is given by ,
the potential energy function is given by
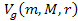 ,
and for reasons of symmetry, the potential energy of each particle
should be the same when the particle masses are exchanged.
Therefore, ,
and for reasons of symmetry, the potential energy of each particle
should be the same when the particle masses are exchanged.
Therefore,
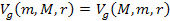 . .
Additionally, at sufficiently large distances, the UG potential
energy equation converges toward Newton’s equation 1-2, which
depends implicitly on the product of the masses of interacting
particles, rather than on their individual masses. There is also no
evidence of strong forces acting between particles where either one
or both particles have zero mass. Therefore, for any particle mass M,
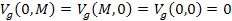 .
This strongly suggests that the potential energy function .
This strongly suggests that the potential energy function
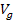 actually depends on only two variables: the distance
actually depends on only two variables: the distance
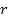 ,
and the product of the two masses ,
and the product of the two masses
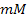 .
Therefore, the second UG postulate can be stated as, .
Therefore, the second UG postulate can be stated as,
UG Postulate II: The unified gravitational force is
a force between a pair of particles. When viewed at an inertial rest
frame of one of the interacting particles (the source particle), the
unified gravitational force applied on the second particle (the test
particle) is predominantly a central and conserving force that
depends exclusively on the absolute distance between the particles
and on the product of their masses.2
This
leads to
Equation
1-2-1
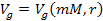
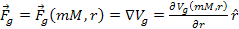
An important question that needs to be addressed is how the UG force
and the UG potential energy depend on the distance
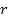 (
(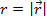 ).
In accordance with the first UG postulate, at large distances3
the UG force equation should asymptotically approach the classical
Newtonian force equation and should fully comply with all
experimental measurements of gravitation that are currently
available, leading to ).
In accordance with the first UG postulate, at large distances3
the UG force equation should asymptotically approach the classical
Newtonian force equation and should fully comply with all
experimental measurements of gravitation that are currently
available, leading to
Equation
1-2-2
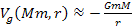 and
and
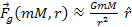 at
at
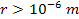
where
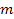 and
and
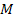 are the masses of ordinary particles such as protons, neutrons and
electrons.
are the masses of ordinary particles such as protons, neutrons and
electrons.
In addition, according to the first postulate, the UG force must
comply with the behavior of the nuclear forces between nucleons,
which have been observed to be substantially stronger than the
Coulomb interaction at below approximately
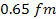 .
Observations further dictate that at distances .
Observations further dictate that at distances
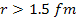 ,
the nuclear force between two protons must be negligible in
comparison to the Coulomb force acting between them. Accordingly, the
UG potential energy must produce an explosive growth at about ,
the nuclear force between two protons must be negligible in
comparison to the Coulomb force acting between them. Accordingly, the
UG potential energy must produce an explosive growth at about
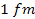 ,
thus leading to the third postulate. ,
thus leading to the third postulate.
UG Postulate III: The UG potential energy has an
exponential dependency on the distance
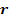 . .
The simplest mathematical function that complies with the
aforementioned requirements is the function
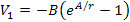 ,
where ,
where
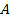 is of the order of
is of the order of
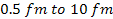 .
This function demonstrates exponential growth, as well as substantial
amplitude at .
This function demonstrates exponential growth, as well as substantial
amplitude at
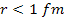 ,
and relatively negligible amplitude at ,
and relatively negligible amplitude at
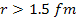 .
In addition, this function and its derivative are practically
indistinguishable from the Newtonian function .
In addition, this function and its derivative are practically
indistinguishable from the Newtonian function
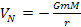 and its derivative at
and its derivative at
 ,
as long as the value of ,
as long as the value of
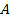 is sufficiently small. Expressed mathematically,
is sufficiently small. Expressed mathematically,
Equation
1-2-3
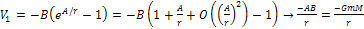 for
for
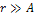
Therefore,
if
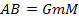 and
and
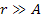 then
then
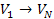 .
Similarly, for the derivative of .
Similarly, for the derivative of
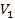 (or the force),
(or the force),
Equation
1-2-4
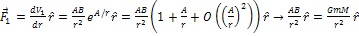
where
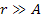 .
Note that while Newton’s force and potential energy equations
depend linearly on the particle mass .
Note that while Newton’s force and potential energy equations
depend linearly on the particle mass
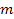 through the product of
through the product of
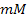 ,
the second UG postulate does not require that the UG force or
potential energy be linear with ,
the second UG postulate does not require that the UG force or
potential energy be linear with
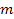 .
Such linearity is possible if the variable .
Such linearity is possible if the variable
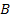 of equation 1-2-3 is proportional to
of equation 1-2-3 is proportional to
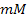 ,
or if ,
or if
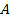 is independent of
is independent of
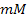 ,
and therefore a constant. However, in order to comply with the first
UG postulate, the UG theory should be capable of explaining the
patterns of nuclear resonances, as well as planetary and galactic
rings patterns, which may consist of many thousands of ringlets, as
observed in Saturn’s complex ring system. Both phenomena
demonstrate strong oscillation patterns. The existence of nuclear
resonances, which demonstrate a series of discrete nuclear energy
levels that depend mainly on the masses of nucleons, strongly
suggests the presence of a shell structure in the nucleus. The
existence of such a shell structure, however, does not necessarily
infer a cyclical UG potential energy. After all, the Coulomb
potential energy of the proton-electron system given by the equation ,
and therefore a constant. However, in order to comply with the first
UG postulate, the UG theory should be capable of explaining the
patterns of nuclear resonances, as well as planetary and galactic
rings patterns, which may consist of many thousands of ringlets, as
observed in Saturn’s complex ring system. Both phenomena
demonstrate strong oscillation patterns. The existence of nuclear
resonances, which demonstrate a series of discrete nuclear energy
levels that depend mainly on the masses of nucleons, strongly
suggests the presence of a shell structure in the nucleus. The
existence of such a shell structure, however, does not necessarily
infer a cyclical UG potential energy. After all, the Coulomb
potential energy of the proton-electron system given by the equation
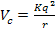 is non-cyclical, but still produces the atomic electron shell
structure due to quantum effects. However, quantum effects occur on
microscopic distance scales and thus cannot be responsible for
planetary or galactic rings, as the large size of the area occupied
by the planetary and galactic rings simply rules them out as a
reasonable cause. Attempts to explain ring structures via
electromagnetic forces have proven to be unsuccessful, and attempts
to explain planetary rings and gaps as a result of orbital
resonances between rings (or the gaps) and certain satellites have
been only partially successful, as they do not explain the vastness
of the ring systems (see Chapter V), nor the entirety of the observed
rings and gaps. In order to provide a mechanism capable of producing
the vast planetary ring systems, as well as the ring and spiral
structures observed in galaxies (see Chapter IV), the UG potential
energy equation must also contain a periodic function. As most of
the gravitational systems familiar to us do not demonstrate cyclical
behavior, the oscillating term must somehow be suppressed at
distances larger than
is non-cyclical, but still produces the atomic electron shell
structure due to quantum effects. However, quantum effects occur on
microscopic distance scales and thus cannot be responsible for
planetary or galactic rings, as the large size of the area occupied
by the planetary and galactic rings simply rules them out as a
reasonable cause. Attempts to explain ring structures via
electromagnetic forces have proven to be unsuccessful, and attempts
to explain planetary rings and gaps as a result of orbital
resonances between rings (or the gaps) and certain satellites have
been only partially successful, as they do not explain the vastness
of the ring systems (see Chapter V), nor the entirety of the observed
rings and gaps. In order to provide a mechanism capable of producing
the vast planetary ring systems, as well as the ring and spiral
structures observed in galaxies (see Chapter IV), the UG potential
energy equation must also contain a periodic function. As most of
the gravitational systems familiar to us do not demonstrate cyclical
behavior, the oscillating term must somehow be suppressed at
distances larger than
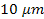 when applied to protons, neutrons and electrons. Whereas nuclear
resonances occur at distances of approximately
when applied to protons, neutrons and electrons. Whereas nuclear
resonances occur at distances of approximately
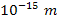 ,
planetary rings occur at distances below ,
planetary rings occur at distances below
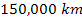 ,
and rings are observed in galaxies at distance ranges of the order of ,
and rings are observed in galaxies at distance ranges of the order of
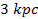 to
to
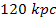 .4
Therefore, the distance range of the oscillations must vary for
different systems, yet must still depend exclusively on the mass of
the interacting particles. Theoretically, ring and galaxy formations
could also be explained by some odd distribution of dark matter, or
by collisions between systems; however, to date these explanations
have provided only limited success for a limited number of systems,
while resulting in models with escalating complexity. Instead, a
different approach is attempted by the UG theory. .4
Therefore, the distance range of the oscillations must vary for
different systems, yet must still depend exclusively on the mass of
the interacting particles. Theoretically, ring and galaxy formations
could also be explained by some odd distribution of dark matter, or
by collisions between systems; however, to date these explanations
have provided only limited success for a limited number of systems,
while resulting in models with escalating complexity. Instead, a
different approach is attempted by the UG theory.
The simplest cyclical function that can concurrently provide
diminished oscillations as
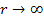 and produce a derivative that, similar to the Newtonian force, is
proportional to
and produce a derivative that, similar to the Newtonian force, is
proportional to
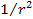 ,
is the function ,
is the function
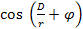 ,
which oscillates at ,
which oscillates at
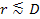 and approaches the constant value
and approaches the constant value
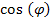 as
as
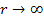 .
If .
If
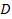 were independent of particle mass, rings should always occur at the
exact same interparticle distances, regardless of the masses of the
two interacting particles, in disagreement with observations that
different planetary and galactic systems often demonstrate concentric
sets of rings at varying radii. This leads to the conclusion that
were independent of particle mass, rings should always occur at the
exact same interparticle distances, regardless of the masses of the
two interacting particles, in disagreement with observations that
different planetary and galactic systems often demonstrate concentric
sets of rings at varying radii. This leads to the conclusion that
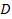 must be dependent on the masses of the particles, or specifically on
their product
must be dependent on the masses of the particles, or specifically on
their product
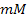 ,
as required by the second postulate. Therefore, the simplest
functions that comply with the above requirements are of the form ,
as required by the second postulate. Therefore, the simplest
functions that comply with the above requirements are of the form
Equation
1-2-5
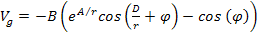
where
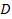 must be dependent on
must be dependent on
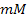 ,
and ,
and
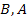 and
and
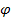 may either be constants or functions of
may either be constants or functions of
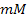 .
The term .
The term
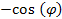 was added to assure that
was added to assure that
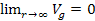 .5
The requirement that at large distances .5
The requirement that at large distances
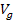 should approach its Newtonian counterpart leads to
should approach its Newtonian counterpart leads to
Equation
1-2-6
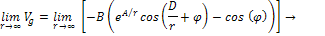
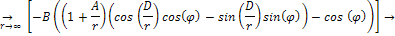
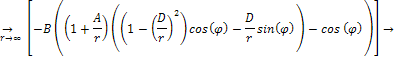
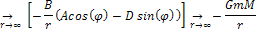
or
Equation
1-2-7
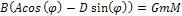
Using
the same process for its derivative (or force),
Equation
1-2-8
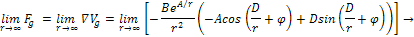
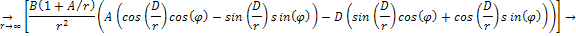
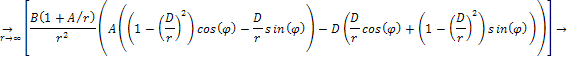
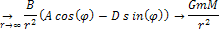
Again, in agreement
with equation 1-2-7,
Equation
1-2-9
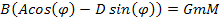
This
leaves us with three degrees of freedom, where setting three out of
the four functions
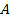 , ,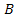 , ,
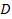 or
or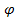 will uniquely determine the fourth function.6
However, there are a few constraints. As discussed above,
will uniquely determine the fourth function.6
However, there are a few constraints. As discussed above,
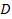 must be dependent on
must be dependent on
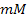 ,
otherwise all planets and galaxies would demonstrate rings at exactly
the same sets of radii. According to equation 1-2-7 (or the
identical equation 1-2-9), either ,
otherwise all planets and galaxies would demonstrate rings at exactly
the same sets of radii. According to equation 1-2-7 (or the
identical equation 1-2-9), either
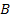 ,
or alternatively ,
or alternatively
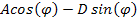 ,
must be equal to or approach zero if either ,
must be equal to or approach zero if either
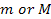 are equal to or approach zero. Therefore, either one or both
are equal to or approach zero. Therefore, either one or both
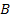 or
or
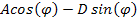 must depend implicitly on
must depend implicitly on
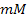 . .
If function
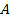 is negative, the UG potential energy would be monotonically
attenuated, becoming zero as
is negative, the UG potential energy would be monotonically
attenuated, becoming zero as
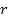 approaches zero. The function
approaches zero. The function
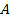 must therefore be positive in order to explain both gravitation and
the strong nuclear interaction. The existence of rings suggests that
the UG cosine term of equation 1-2-5 oscillates within the radius of
the farthest observed ring, requiring that
must therefore be positive in order to explain both gravitation and
the strong nuclear interaction. The existence of rings suggests that
the UG cosine term of equation 1-2-5 oscillates within the radius of
the farthest observed ring, requiring that
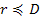 .
The fact that gravitational fields do not demonstrate explosive
exponential growth in the vicinity of the observed galactic or
planetary rings further requires that within the distance range of
the rings, .
The fact that gravitational fields do not demonstrate explosive
exponential growth in the vicinity of the observed galactic or
planetary rings further requires that within the distance range of
the rings,
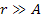 .
In the range of distances .
In the range of distances
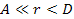 ,
equation 1-2-5 can be reduced to ,
equation 1-2-5 can be reduced to
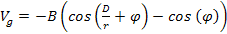 ,
and therefore oscillates with virtually constant amplitude ,
and therefore oscillates with virtually constant amplitude
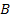 .
It is reasonable to assume that particles of greater mass should
produce a larger UG potential energy amplitude within this
oscillation range. This suggests that B should also be dependent on .
It is reasonable to assume that particles of greater mass should
produce a larger UG potential energy amplitude within this
oscillation range. This suggests that B should also be dependent on
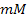 .
While these constraints eliminate many possible combinations of
functions .
While these constraints eliminate many possible combinations of
functions
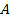 , ,
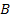 , ,
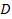 and
and
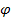 ,
a substantial number of possibilities remain, and a significant
amount of experimental data is required before the number of possible
equations can be reduced to a bare minimum. However, once the values
of ,
a substantial number of possibilities remain, and a significant
amount of experimental data is required before the number of possible
equations can be reduced to a bare minimum. However, once the values
of
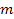 and
and
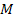 are set,
are set,
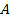 , ,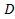 and
and
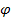 can be treated as a set of constants (denoted
can be treated as a set of constants (denoted
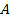 , ,
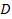 and
and
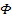 )
and equation 1-2-5 becomes )
and equation 1-2-5 becomes
Equation
1-2-10
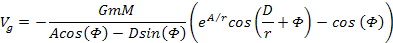
Among the mathematically possible sets of functions
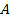 , ,
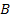 , ,
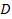 and
and
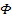 ,
the simplest and most logical are those where the exponent operand ,
the simplest and most logical are those where the exponent operand
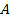 is a positive constant
is a positive constant
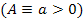 and the phase
and the phase
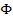 is set as zero. This leads to
is set as zero. This leads to
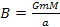 .
As .
As
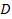 must depend on the particle masses,
must depend on the particle masses,
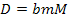 is selected for simplicity, where
is selected for simplicity, where
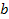 is a constant.
is a constant.
Using this simplified set, the UG potential energy can be written
as
Equation
1-2-11
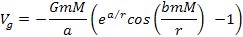
Equation 1-2-11 was derived by searching for the simplest function
that is compatible with the UG postulates. While in agreement with
the spirit of Occam’s Razor, the selection of the simplest
equation is somewhat subjective, and cannot necessarily be regarded
as proven. After all, nature is not required to guarantee
simplicity. However, the simplest model is usually a good starting
point. If experimental data is found to conflict with the
predictions of equation 1-2-11, new sets of functions should be
evaluated.
The inclusion of a cosine term (or in general, a cyclical term) in
the UG equation, and the dependency of its operand on the particle
masses, is probably the most fundamental deviation of the UG theory
from Newton’s theory and general relativity. According to
Newton’s equation, the external gravitational force applied on
an object is always an attractive force that is linearly proportional
to its total mass
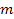 .
Newton’s gravitational theory holds that the external force is
the same whether a point-like object consists of few heavy
fundamental particles or of many light fundamental particles, as long
as the total sum of all of their masses are the same. For example,
according to the Newtonian equation, the gravitational force applied
by an external point-like and electromagnetically neutral object of
mass .
Newton’s gravitational theory holds that the external force is
the same whether a point-like object consists of few heavy
fundamental particles or of many light fundamental particles, as long
as the total sum of all of their masses are the same. For example,
according to the Newtonian equation, the gravitational force applied
by an external point-like and electromagnetically neutral object of
mass
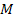 on a point-like object containing a single particle of mass
on a point-like object containing a single particle of mass
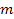 is virtually equal to the gravitational force applied by the same
external object from the same distance on a point-like object
containing
is virtually equal to the gravitational force applied by the same
external object from the same distance on a point-like object
containing
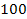 particles of mass
particles of mass
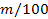 .
The UG theory makes the distinction that the UG force is linear with
the number of fundamental particles if they are all of the same mass.
However, the UG force and potential energy are not linear functions
of the fundamental particle masses, and therefore are not necessarily
linear with the total mass of the object. As an example, the
Newtonian gravitational potential energy .
The UG theory makes the distinction that the UG force is linear with
the number of fundamental particles if they are all of the same mass.
However, the UG force and potential energy are not linear functions
of the fundamental particle masses, and therefore are not necessarily
linear with the total mass of the object. As an example, the
Newtonian gravitational potential energy
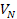 between two atoms, one containing
between two atoms, one containing
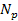 protons,
protons,
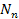 neutrons and
neutrons and
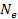 electrons of respective mass
electrons of respective mass
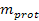 , ,
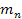 and
and
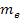 and the other containing
and the other containing
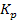 protons,
protons,
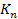 neutrons and
neutrons and
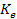 electrons, is given by
electrons, is given by
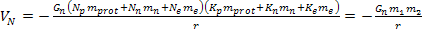 ,
where the distance ,
where the distance
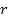 between the two atoms is assumed to be significantly larger than the
diameter of either atom.7
The total mass of each atom is given by
between the two atoms is assumed to be significantly larger than the
diameter of either atom.7
The total mass of each atom is given by
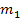 and
and
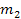 ,
and ,
and
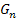 is the Newtonian gravitational constant.
is the Newtonian gravitational constant.
The UG potential energy
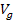 of the same interaction is provided by
of the same interaction is provided by
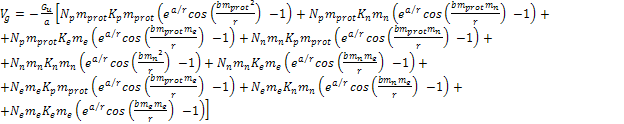
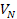 and
and
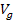 are not identical at sufficiently short distances where
are not identical at sufficiently short distances where
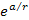 is distinguishable from
is distinguishable from
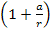 ,
or if ,
or if
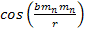 is
still oscillating or has not yet converged to is
still oscillating or has not yet converged to
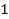 .8
At these distance ranges, the cosine terms within .8
At these distance ranges, the cosine terms within
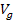 are not all equal, and the total sum within the brackets does not add
up to the product of the overall mass of the atoms. At large
distances, where
are not all equal, and the total sum within the brackets does not add
up to the product of the overall mass of the atoms. At large
distances, where
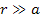 and
and
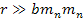 , ,
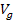 does converge toward
does converge toward
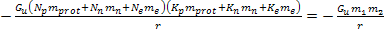 , and with
, and with
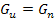 ,
the two potential energies converge. ,
the two potential energies converge.
Therefore, with a constant
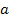 that is significantly less than the diameter of a hydrogen atom, and
with a constant b that complies with
that is significantly less than the diameter of a hydrogen atom, and
with a constant b that complies with
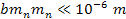 ,
the two potential energy functions are indistinguishable at distances
greater than ,
the two potential energy functions are indistinguishable at distances
greater than
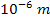 .
However, for interactions involving fundamental particles of a mass
significantly larger than the mass of a proton or neutron, the
deviation from the Newtonian equation would become significant at
greater distance ranges. Theoretically, these distances can extend
to tens of thousands of kilometers if sufficiently large fundamental
particles exist at the center of planets, or may further extend to
the order of tens of .
However, for interactions involving fundamental particles of a mass
significantly larger than the mass of a proton or neutron, the
deviation from the Newtonian equation would become significant at
greater distance ranges. Theoretically, these distances can extend
to tens of thousands of kilometers if sufficiently large fundamental
particles exist at the center of planets, or may further extend to
the order of tens of
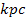 if substantially heavier particles exist at the galactic centers,
leading to the fourth UG postulate.
if substantially heavier particles exist at the galactic centers,
leading to the fourth UG postulate.
UG Postulate IV: The extreme temperature and pressure
conditions that exist at the cores of entities such as planets,
stars and galaxies produce relatively stable superheavy
particles (SHPs). Substantially higher temperature and
pressure produce substantially more massive fundamental particles.
The production of very massive fundamental particles, coupled with
the UG equations (equations 1-2-5, 1-2-10 or 1-2-11), can provide a
mechanism for generating planetary or galactic rings within the
distance range where the cosine term demonstrates oscillations.
High-energy collisions between electrons and positrons have been
shown to create particles that are heavier than
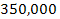 times
their mass. Consistent with postulate IV, experimental data shows
that higher energy particle collisions are capable of producing more
massive particles. However, the masses of the heaviest particles
produced via collision experiments are far smaller than the extreme
masses required for the production of planetary or galactic rings via
equation 1-2-11. Furthermore, the heaviest particles produced by
high-energy collision experiments exist for only an instant before
decaying into a barrage of lighter particles. Note, however, that
the energy levels at the cores of planets, stars and galaxies are
many orders of magnitude greater than those created by particle
accelerators, and therefore the postulation that they can produce
particles of substantially greater mass is logical. The relative
stability of planetary ring systems suggests that if rings are in
fact produced by superheavy particles in the vicinity of the central
core of a planet, then the number of superheavy particles involved
must be about constant. This can be explained via two different
processes. First, the steady-state conditions within the core of a
planet dictate that on average, the rate of production of a
particular type of SHP should be equal to its rate of decay. Second,
although free neutrons are known to be unstable and to decay, a
neutron becomes stable when bonded with a proton in an atom nucleus.
A similar mechanism may be at work for the large superheavy
particles within galactic, stellar or planetary cores, where the
superheavy particles may become bonded to each other or to the
central core of ordinary matter, and thus become stable.9
A more restrictive assertion, known as quark confinement, is made by
the standard model, in which quarks are assumed to be stable only
when they are bonded together. times
their mass. Consistent with postulate IV, experimental data shows
that higher energy particle collisions are capable of producing more
massive particles. However, the masses of the heaviest particles
produced via collision experiments are far smaller than the extreme
masses required for the production of planetary or galactic rings via
equation 1-2-11. Furthermore, the heaviest particles produced by
high-energy collision experiments exist for only an instant before
decaying into a barrage of lighter particles. Note, however, that
the energy levels at the cores of planets, stars and galaxies are
many orders of magnitude greater than those created by particle
accelerators, and therefore the postulation that they can produce
particles of substantially greater mass is logical. The relative
stability of planetary ring systems suggests that if rings are in
fact produced by superheavy particles in the vicinity of the central
core of a planet, then the number of superheavy particles involved
must be about constant. This can be explained via two different
processes. First, the steady-state conditions within the core of a
planet dictate that on average, the rate of production of a
particular type of SHP should be equal to its rate of decay. Second,
although free neutrons are known to be unstable and to decay, a
neutron becomes stable when bonded with a proton in an atom nucleus.
A similar mechanism may be at work for the large superheavy
particles within galactic, stellar or planetary cores, where the
superheavy particles may become bonded to each other or to the
central core of ordinary matter, and thus become stable.9
A more restrictive assertion, known as quark confinement, is made by
the standard model, in which quarks are assumed to be stable only
when they are bonded together.
We must also question whether it is reasonable to assume the
possibility of the existence of fundamental particles of masses of
many orders of magnitude greater than the most massive particle ever
observed (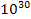 times heavier). To answer this question we should bear in mind that
according to the UG postulate IV, such large particles can be
produced and maintained only within violent environments of extremely
high energy, temperature and pressure, as exist at the cores of
planets, stars and galaxies. These violent environments are simply
not accessible for direct and close observation. However, according
to the UG theory, their effects can be observed from far distances in
the form of planetary rings, ring and spiral galaxies, and as
rejection forces that drive galaxies away from each other. The idea
that a gravitational collapse could generate massive superheavy
particles of many orders of magnitude larger than the heaviest
particles observed can understandably be viewed as almost
inconceivable. It should be noted, however, that this postulate is
very mild relative to the accepted notion of the existence of black
holes. According to the no-hair theorem,10
a black hole is viewed by an external observer to behave like a
particle with enormous mass. However, the masses of black holes,
which are believed to be produced by gravitational collapse, may
exceed the SHP masses contemplated here by factors of
times heavier). To answer this question we should bear in mind that
according to the UG postulate IV, such large particles can be
produced and maintained only within violent environments of extremely
high energy, temperature and pressure, as exist at the cores of
planets, stars and galaxies. These violent environments are simply
not accessible for direct and close observation. However, according
to the UG theory, their effects can be observed from far distances in
the form of planetary rings, ring and spiral galaxies, and as
rejection forces that drive galaxies away from each other. The idea
that a gravitational collapse could generate massive superheavy
particles of many orders of magnitude larger than the heaviest
particles observed can understandably be viewed as almost
inconceivable. It should be noted, however, that this postulate is
very mild relative to the accepted notion of the existence of black
holes. According to the no-hair theorem,10
a black hole is viewed by an external observer to behave like a
particle with enormous mass. However, the masses of black holes,
which are believed to be produced by gravitational collapse, may
exceed the SHP masses contemplated here by factors of
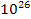 to
to
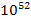 .
Therefore, to make it easier to comprehend the fourth postulate in
terms of current belief, the postulate can be described as an
assumption that the extreme conditions generated by the collapse of
gas clouds produces small black holes (SHPs) near the center of the
planet, star or galaxy. With this approach, the main and fundamental
difference between the UG theory and the current paradigm (Newton’s
gravitational theory and general relativity) is the use of equation
1-2-11, rather than equation 1-2, to describe the potential energy of
the interaction. .
Therefore, to make it easier to comprehend the fourth postulate in
terms of current belief, the postulate can be described as an
assumption that the extreme conditions generated by the collapse of
gas clouds produces small black holes (SHPs) near the center of the
planet, star or galaxy. With this approach, the main and fundamental
difference between the UG theory and the current paradigm (Newton’s
gravitational theory and general relativity) is the use of equation
1-2-11, rather than equation 1-2, to describe the potential energy of
the interaction.
|



