Nebulae and
galaxies are observed to come in many shapes and sizes. This raises
the question of whether the morphology observed for an astronomical
object of a given size can recur in astronomical objects on an
entirely different distance scale. As satellites, planets, stars,
nebulae, galaxies and clusters of galaxies are assumed to be governed
by the same gravitational law, it is logical to suppose that the same
morphology can be observed across distance scales. According to the
UG theory, for any given system consisting of a test object that
rotates around a source object with an orbital radius significantly
larger than the constant
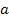 (approximately larger than the size of an atom), the following UG
scaling theorem can be applied:
(approximately larger than the size of an atom), the following UG
scaling theorem can be applied:
A-1: The First UG
Scaling Theorem
Consider a system
containing a test object with
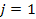 to
to
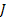 groups of
groups of
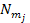 particles
of mass particles
of mass
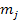 located at
located at
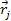 moving at velocities
moving at velocities
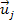 relative to the center of the source object. The source object
contains
relative to the center of the source object. The source object
contains
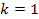 to
to
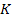 groups of
groups of
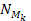 particles
of mass particles
of mass
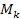 located at
located at
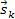 moving at velocities of
moving at velocities of
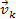 relative to its center.1
The UG potential energy of the test object is therefore given by
relative to its center.1
The UG potential energy of the test object is therefore given by
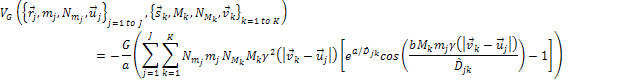
The UG potential
energy between the two objects of the system scaled via
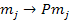 , ,
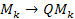 , ,
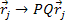 and
and
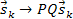 ,
where ,
where
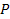 and
and
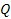 are rational numbers2
and all velocities
are rational numbers2
and all velocities
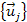 and
and
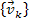 remain unaltered, yields
remain unaltered, yields
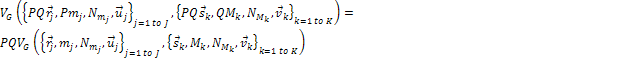
where
the angular velocity of any particle in the scaled system is reduced
by a factor of
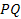 (
(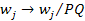 and
and
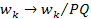 ). ). Proof: Denote
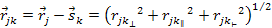 and
and
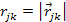 ,
where within the plane defined by the vectors ,
where within the plane defined by the vectors
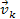 and and
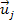 , ,
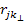 is
the is
the
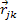 component that is perpendicular to the vector
component that is perpendicular to the vector
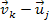 , ,
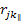 is the
is the
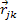 component that is parallel to the vector
component that is parallel to the vector
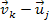 within the plane, and
within the plane, and
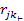 is the
is the
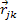 component that is perpendicular to the plane. Since only the
parallel component of
component that is perpendicular to the plane. Since only the
parallel component of
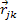 is contracted by the relativistic effect, the distance between the
two particles, as viewed in the inertial frame of either particle, is
given by
is contracted by the relativistic effect, the distance between the
two particles, as viewed in the inertial frame of either particle, is
given by 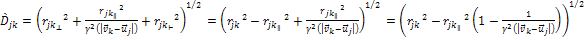
with
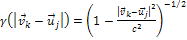 .
Thus, .
Thus,
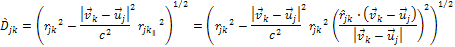
or 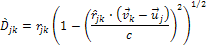
On
scales significantly larger than nuclear scale, the distance between
the two objects is substantially greater than
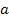 ;
hence, ;
hence,
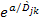 becomes indistinguishable from
becomes indistinguishable from
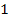 .
Therefore, .
Therefore, Equation
A-1-1 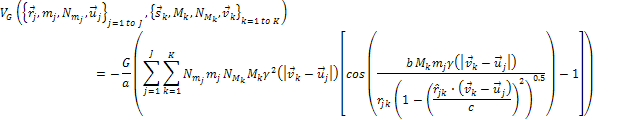
Scaling
 , ,
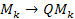 , ,
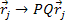 and
and
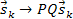 and using the identity
and using the identity
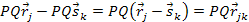 ,
while retaining the same sets of velocities ,
while retaining the same sets of velocities
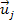 and
and
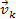 ,
provides ,
provides Equation
A-1-3 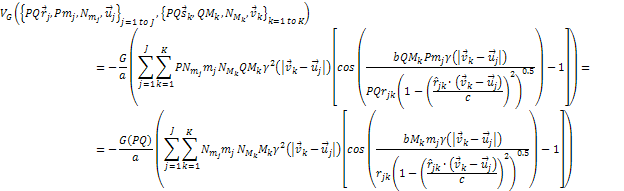
Thus,
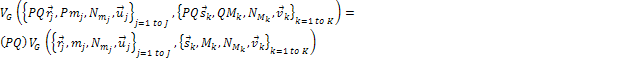 as claimed in the
first part of the first theorem. Note that for the
first theorem to hold true, the set of velocities
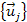 and
and
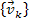 must remain unchanged.3
In the contrary case, the terms
must remain unchanged.3
In the contrary case, the terms
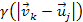 and
and
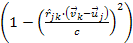 would cause significant distortion in the scaled system. Therefore,
to preserve the morphology, all the particles of the scaled system
must travel at the same velocity as their counterparts in the
original system. In the case of solid rotation, where a group of
particles (within either object of the original system) rotate as a
solid sub-object around the center of the source object with an
angular momentum
would cause significant distortion in the scaled system. Therefore,
to preserve the morphology, all the particles of the scaled system
must travel at the same velocity as their counterparts in the
original system. In the case of solid rotation, where a group of
particles (within either object of the original system) rotate as a
solid sub-object around the center of the source object with an
angular momentum
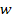 ,
the group of particles travels at a velocity of ,
the group of particles travels at a velocity of
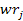 (or
(or
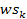 ).
As ).
As
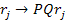 and
and
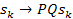 the angular velocity of the scaled sub-object must be scaled to
the angular velocity of the scaled sub-object must be scaled to
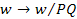 in order for the velocity of the particles of the scaled system to
equal the velocity of the particles of the original system. While
different sections of the original system may demonstrate different
angular velocities, all the angular velocities of all of the
particles in the scaled system must be reduced by the same factor of
in order for the velocity of the particles of the scaled system to
equal the velocity of the particles of the original system. While
different sections of the original system may demonstrate different
angular velocities, all the angular velocities of all of the
particles in the scaled system must be reduced by the same factor of
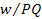 ,
proving the second part of the first theorem. ,
proving the second part of the first theorem.
A-2: The Second
UG Scaling Theorem The
potential energy is linear with the number of particles of each type. Therefore,
scaling up the number of particles of all the groups within the test
or the source objects by factors of 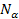 and
and 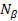 respectively yields
respectively yields
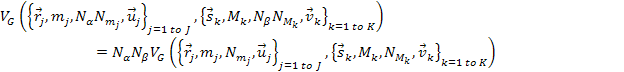
Proof:
Equation
A-1-4 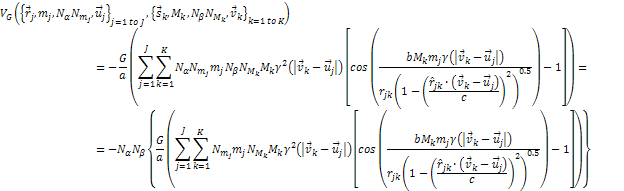
Thus, 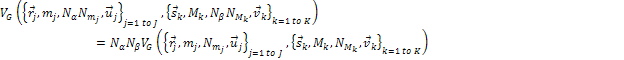
Note
that in contrast to the first theorem, the second theorem is valid at
all distances, including the nuclear range where
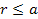 . .
1
Note that this description is sufficiently general to describe any
real astronomical system, as it is always possible to select the
SHP groups in such a way
that each one includes only a single particle. Thus, 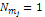 and and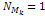 for all
for all 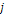 and
and 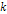 ,
and the number of particles in the system is equal to ,
and the number of particles in the system is equal to 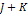 . . 2
Although the values of  and
and 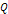 can mathematically be any real number,
can mathematically be any real number,  and
and 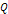 only have a physical meaning as integers or rational numbers, since
the number of particles must be given by an integer.
only have a physical meaning as integers or rational numbers, since
the number of particles must be given by an integer. 3
Note that in the case where all of the particles of the original
system as well as the scaled system are non-relativistic, the
theorem can be extended to allow for the scaling of all velocities
by a fixed factor 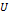 ,
where ,
where 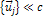 , ,
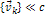 , ,
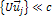 ,
and ,
and 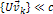 .
In such a case, the morphology
of the system will remain unaltered, while all of its angular
velocities will increase by a factor of .
In such a case, the morphology
of the system will remain unaltered, while all of its angular
velocities will increase by a factor of  . .
|



