Deep
inelastic scattering experiments (DIS) provided the initial
motivation for the development of a hadron constituent model. Deep
inelastic electron-proton scattering experiments of the 1960s1
revealed a surprising weak fall-off of the deep inelastic cross
sections with increasing
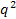 and exhibited a scaling behavior previously predicted by Bjorken
(Bjorken, 1969). Both observations strongly suggested
the existence of a substructure in protons and neutrons. A preceding
constituent model proposed by Richard Feynman offered a simple
dynamical interpretation of the DIS results. Feynman postulated
partons as the elementary constituents of hadrons, yet specified
their identity only as far as basic particles relating under the
strong interaction. Further development linked the parton model with
the concept of quarks. Quarks, which were proposed independently by
Gell-Mann (Gell-Mann, 1964) and Zweig as mathematically
convenient building blocks of unitary symmetry, were the natural
candidates for these elementary constituents. The early constituent
quark model faced significant obstacles. To begin with, quarks had
never been observed directly. The fact that quarks were never
observed should have been explained by very strong interactions in
their final state. The theory, however, required that the
constituents of hadrons behave as free particles during virtual
photon absorption. In addition, experimental results demanded
significantly more than three constituents within the nucleon
substructure. Resolving these, as well as additional
inconsistencies, led to enhancements in the quark model and to the
development of quantum chromodynamics (QCD). This resulted in a
powerful, yet significantly more complex theory, postulating the
additional concepts of gluons, colors, sea of quarks, quark
confinement and the property of asymptotic freedom, with heavy
reliance on renormalization techniques.
and exhibited a scaling behavior previously predicted by Bjorken
(Bjorken, 1969). Both observations strongly suggested
the existence of a substructure in protons and neutrons. A preceding
constituent model proposed by Richard Feynman offered a simple
dynamical interpretation of the DIS results. Feynman postulated
partons as the elementary constituents of hadrons, yet specified
their identity only as far as basic particles relating under the
strong interaction. Further development linked the parton model with
the concept of quarks. Quarks, which were proposed independently by
Gell-Mann (Gell-Mann, 1964) and Zweig as mathematically
convenient building blocks of unitary symmetry, were the natural
candidates for these elementary constituents. The early constituent
quark model faced significant obstacles. To begin with, quarks had
never been observed directly. The fact that quarks were never
observed should have been explained by very strong interactions in
their final state. The theory, however, required that the
constituents of hadrons behave as free particles during virtual
photon absorption. In addition, experimental results demanded
significantly more than three constituents within the nucleon
substructure. Resolving these, as well as additional
inconsistencies, led to enhancements in the quark model and to the
development of quantum chromodynamics (QCD). This resulted in a
powerful, yet significantly more complex theory, postulating the
additional concepts of gluons, colors, sea of quarks, quark
confinement and the property of asymptotic freedom, with heavy
reliance on renormalization techniques.
The
quark and QCD models seem to provide adequate explanations for all
available experimental data. Therefore, a choice has been made to
first establish the credibility of the UG theory in the cosmic realm,
where inconsistencies within the current theory are well documented.
In this chapter, the UG theory will be employed on nuclear scale. It
will be shown that the UG zonal structure generated by the
interaction between two massive particles creates a dynamic
substructure that naturally leads to the observed large-angle
scattering, as well as to the weak fall-off of the DIS cross section,
and provides a scaling phenomenon that resembles Bjorken scaling.
Since the substructure is due to the interaction between a pair of
particles, rather than due to constituent sub-particles, the UG
theory does not require the assumption of quarks as real elementary
particles.2 Since
the acceptance of quantum chromodynamics in the early 1970s, the
quark structure of hadrons has become the dominant framework for
theory development and experimental design. As a result, a
significant portion of data collected from deep inelastic scattering
has generally been analyzed within this framework, and reflects its
embedded assumptions. Some parameters commonly used in data
presentation are Equation
11-1 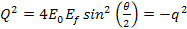
and Equation
11-2 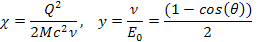
where
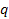 denotes the four-momentum transfer function,
denotes the four-momentum transfer function,
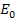 represents the energy of the incident lepton, represents the energy of the incident lepton,
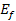 represents the energy of the scattered lepton, represents the energy of the scattered lepton,
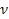 provides the energy loss of the scattered lepton, or
provides the energy loss of the scattered lepton, or
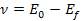 , ,
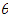 indicates the scattering angle,
indicates the scattering angle,
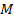 is the mass of the nucleon,
is the mass of the nucleon,
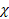 is the Bjorken scale variable,
is the Bjorken scale variable,
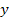 provides the fraction of the leptonís energy loss in the rest
frame of the nucleon, and
provides the fraction of the leptonís energy loss in the rest
frame of the nucleon, and
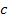 is the speed of light. Reported experimental data commonly provides
the values of the nucleon structure functions
is the speed of light. Reported experimental data commonly provides
the values of the nucleon structure functions
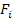 as functions of some of the above parameters, as demonstrated in
figure 11-7. According to the quark-QCD model, in the case of a
high-energy DIS mediated by virtual photon exchange, the structure
functions relate to the double differential cross section via the
equation (see Devenish & Cooper-Sarkar, 2004)
as functions of some of the above parameters, as demonstrated in
figure 11-7. According to the quark-QCD model, in the case of a
high-energy DIS mediated by virtual photon exchange, the structure
functions relate to the double differential cross section via the
equation (see Devenish & Cooper-Sarkar, 2004) Equation
11-3 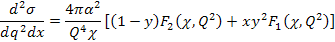
where
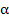 is the fine structure constant. The experimental data is often
presented in the form of the nucleon structure functions
is the fine structure constant. The experimental data is often
presented in the form of the nucleon structure functions
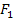 and
and
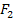 after being subjected to a series of data processing routines, such
as radiative corrections and Monte Carlo simulations, which are
heavily dependent on the assumptions of the QCD model. The
incorporation of these underlying assumptions within the data
complicates the ability to apply the data to a new theory with an
entirely different set of assumptions. Therefore, the following
discussion will present evidence that the UG theory predicts DIS
behavior using a related, yet not identical set of parameters.
after being subjected to a series of data processing routines, such
as radiative corrections and Monte Carlo simulations, which are
heavily dependent on the assumptions of the QCD model. The
incorporation of these underlying assumptions within the data
complicates the ability to apply the data to a new theory with an
entirely different set of assumptions. Therefore, the following
discussion will present evidence that the UG theory predicts DIS
behavior using a related, yet not identical set of parameters. According
to the QCD model, the strong force acts between quarks and is
mediated by gluons, while lepton-nucleon interactions are viewed as
an electromagnetic interaction between charged leptons and charged
quarks within the nucleons. Therefore, according to quantum
chromodynamics, the fundamental process in DIS experiments is the
electromagnetic scattering of two spin-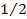 point-like particles. In contrast, the UG model holds that there is
no fundamental difference in the interactions between two nucleons,
two leptons, or interactions involving a lepton and a nucleon. All
of the above particles have a charge,3
a mass and a spin, and are assumed to interact with each other in
accordance with the theory of unified gravitation and the
electromagnetic theory.4
According to the proposed UG model, the large scattering angles
observed in high-energy collisions between a nucleon and a lepton are
mainly attributed to the UG zone structure between the two colliding
particles, rather than to electromagnetic interactions between the
lepton and a hadron with a substructure composed of several
elementary constituents. Historically, the quark-parton model (QPM)
grew out of an attempt to provide a simple model to explain the
results of the early deep inelastic scattering experiments, where the
function
point-like particles. In contrast, the UG model holds that there is
no fundamental difference in the interactions between two nucleons,
two leptons, or interactions involving a lepton and a nucleon. All
of the above particles have a charge,3
a mass and a spin, and are assumed to interact with each other in
accordance with the theory of unified gravitation and the
electromagnetic theory.4
According to the proposed UG model, the large scattering angles
observed in high-energy collisions between a nucleon and a lepton are
mainly attributed to the UG zone structure between the two colliding
particles, rather than to electromagnetic interactions between the
lepton and a hadron with a substructure composed of several
elementary constituents. Historically, the quark-parton model (QPM)
grew out of an attempt to provide a simple model to explain the
results of the early deep inelastic scattering experiments, where the
function
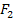 was discovered to be independent of
was discovered to be independent of
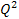 at
at
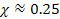 .
QPM assumes that the nucleon consists of non-interacting point-like
particles which serve as scattering centers. In contrast, according
to the UG model, the UG gravitational field produced by the
interaction between a rapidly approaching particle and a nucleon is
viewed by the particle as an Ďonioní with an infinite
number of repulsive layers separated by attractive layers, where the
layers consist of the potential energy maxima or minima respectively.
It will further be demonstrated that due to relativistic spacetime
distortion, the shape and size of the Ďonioní and its
layers are strongly affected by the momentary speed of the
approaching particle, and may change drastically as the speed of the
particle is reduced near the point of closest approach during a DIS
event. The number of layers penetrated by the electron will be shown
to depend mainly on the initial energy of the probing particle and on
its impact parameter. Therefore, the idea of scattering by a sea of
quarks is replaced by the concept of scattering via some of an
infinite number of UG zones, where the zonal indices that contribute
to the scattering are mainly determined by the impact parameter and
by the overall energy of the probing particle. .
QPM assumes that the nucleon consists of non-interacting point-like
particles which serve as scattering centers. In contrast, according
to the UG model, the UG gravitational field produced by the
interaction between a rapidly approaching particle and a nucleon is
viewed by the particle as an Ďonioní with an infinite
number of repulsive layers separated by attractive layers, where the
layers consist of the potential energy maxima or minima respectively.
It will further be demonstrated that due to relativistic spacetime
distortion, the shape and size of the Ďonioní and its
layers are strongly affected by the momentary speed of the
approaching particle, and may change drastically as the speed of the
particle is reduced near the point of closest approach during a DIS
event. The number of layers penetrated by the electron will be shown
to depend mainly on the initial energy of the probing particle and on
its impact parameter. Therefore, the idea of scattering by a sea of
quarks is replaced by the concept of scattering via some of an
infinite number of UG zones, where the zonal indices that contribute
to the scattering are mainly determined by the impact parameter and
by the overall energy of the probing particle.
The
following analysis deals with a DIS collision between a nucleon and
an electron. Note that the discussion is not limited to a collision
between an electron and a nucleon, and may be extended to cover
collisions between any two leptons, two nucleons, a lepton and a
nucleon, or between any two massive particles. However, the
discussion is limited to cases where the probing particle survives
the collision.
Section XI-1-1:
The Effect of the Velocity of Colliding Particles on Their UG
Interaction
Based
on the second UG postulate, equation 2-1-1 is valid when the
interaction between a nucleon and an electron is viewed in the rest
frame of the nucleon. For simplicity, the origin of the frame is set
to coincide with the location of the nucleon. According to special
relativity, the rest mass of the electron
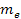 and the distance
and the distance
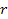 should be replaced by
should be replaced by
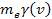 and
and
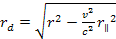 respectively,5
where
respectively,5
where
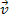 is the velocity of the electron relative to the nucleon and
is the velocity of the electron relative to the nucleon and
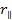 is the distance component that is parallel to
is the distance component that is parallel to
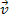 .
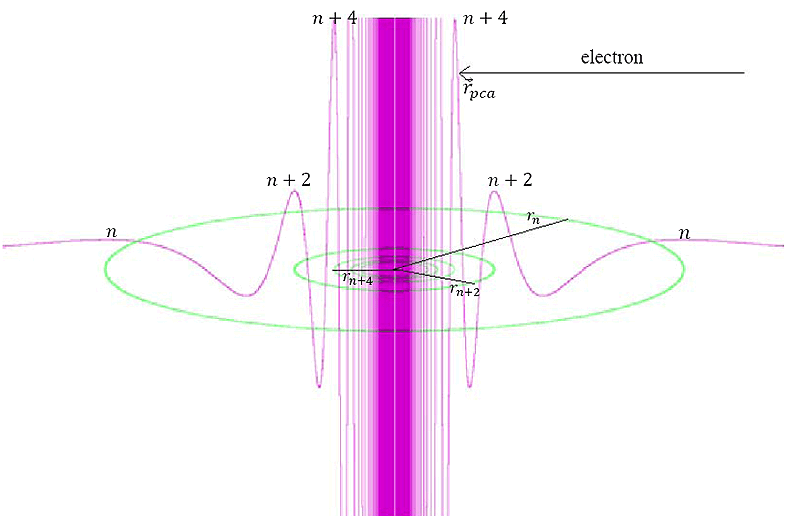
Figure 11-1 provides the initial geometry of an electron-nucleon
scattering, where a highly relativistic electron with the initial
velocity of .
Figure 11-1 provides the initial geometry of an electron-nucleon
scattering, where a highly relativistic electron with the initial
velocity of
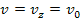 and an impact parameter of
and an impact parameter of
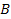 approaches the nucleon. The contribution of the nucleon to the UG
potential energy of the electron is given by6
approaches the nucleon. The contribution of the nucleon to the UG
potential energy of the electron is given by6 Equation
11-4 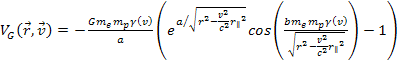
where
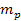 is the rest mass of the nucleon and
is the rest mass of the nucleon and
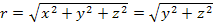 when the
when the
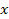 axis is selected to be perpendicular to the plane containing the
vectors
axis is selected to be perpendicular to the plane containing the
vectors
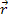 and
and
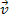 .
Note that at non-relativistic velocities, or when the vectors .
Note that at non-relativistic velocities, or when the vectors
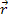 and
and
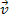 are perpendicular,
are perpendicular,
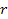 coincides with the distance between the electron and the nucleon. At
relativistic velocities, the true distance between these two
particles is less than
coincides with the distance between the electron and the nucleon. At
relativistic velocities, the true distance between these two
particles is less than
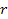 ,
and is further dependent on the magnitude and the direction of the
relative velocity ,
and is further dependent on the magnitude and the direction of the
relative velocity
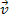 .
According to special relativity, only the distance component that is
parallel to the relative velocity is contracted. This parallel
component is given by .
According to special relativity, only the distance component that is
parallel to the relative velocity is contracted. This parallel
component is given by Equation
11-5 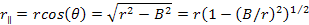
Therefore, the
variable
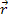 (or
(or
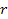 )
should be considered as a parameter of the electronís
trajectory, rather than the distance between the electron and the
nucleon. In cases where the velocities are relativistic (and
therefore, )
should be considered as a parameter of the electronís
trajectory, rather than the distance between the electron and the
nucleon. In cases where the velocities are relativistic (and
therefore,
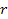 may not be equal to the actual distance as viewed in the inertial
frame of the nucleon)
may not be equal to the actual distance as viewed in the inertial
frame of the nucleon)
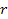 will be referred to as the parametric distance, while the actual
distance viewed in the nucleonís inertial frame of reference
will be referred to as the apparent distance. At distances where
will be referred to as the parametric distance, while the actual
distance viewed in the nucleonís inertial frame of reference
will be referred to as the apparent distance. At distances where
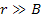 , ,
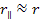 ,
and equation 11-4 reduces to ,
and equation 11-4 reduces to Equation
11-6 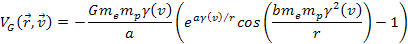
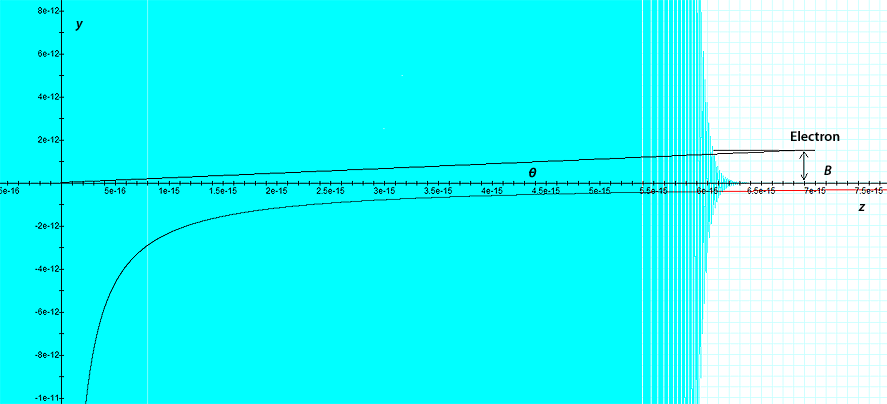
Figure
11-1a: An electron
with an impact parameter
of B
approaches the nucleon at a velocity that corresponds with 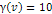 in the direction parallel to the
in the direction parallel to the 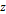 axis. At this speed, the potential energy due to the UG force is
provided in cyan and the electromagnetic force
is provided in red for the case where the nucleon is a proton. The
UG pattern (cyan) remains stable as long as the electron
is located at sufficient distance from the nucleon and its velocity
is about constant. As the electron
approaches the nucleon, its UG potential energy increases abruptly to
equal the overall energy of the electron
(at about
axis. At this speed, the potential energy due to the UG force is
provided in cyan and the electromagnetic force
is provided in red for the case where the nucleon is a proton. The
UG pattern (cyan) remains stable as long as the electron
is located at sufficient distance from the nucleon and its velocity
is about constant. As the electron
approaches the nucleon, its UG potential energy increases abruptly to
equal the overall energy of the electron
(at about 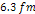 ),
causing the electron to
decelerate. As the electronís
velocity is reduced, the UG pattern and the Coulomb
potential energy collapse toward the proton, demonstrating the
folding of the zonal
structure described in section XI-2-2. ),
causing the electron to
decelerate. As the electronís
velocity is reduced, the UG pattern and the Coulomb
potential energy collapse toward the proton, demonstrating the
folding of the zonal
structure described in section XI-2-2.
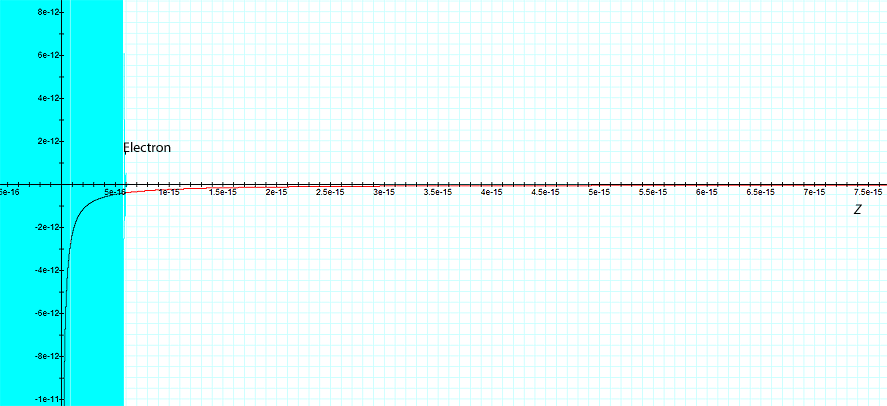
Figure
11-1b: Provides the
contributions of the UG and the electromagnetic potential energy
patterns as perceived by the electron
after its speed is reduced to non-relativistic velocity, where 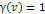 . .
Of
special interest is the point of closest approach
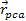 of the electron to the nucleon, measured in the particle
acceleratorís frame of reference. As
of the electron to the nucleon, measured in the particle
acceleratorís frame of reference. As
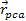 is the closest point on the electronís trajectory toward the
nucleon, its parallel component
is the closest point on the electronís trajectory toward the
nucleon, its parallel component
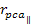 must be equal to zero, and the perpendicular component
must be equal to zero, and the perpendicular component
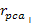 must
be equal to must
be equal to
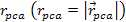 .
Therefore, in the vicinity of the point of closest approach,
equation 11-4 reduces to .
Therefore, in the vicinity of the point of closest approach,
equation 11-4 reduces to Equation
11-7 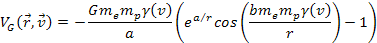
At non-relativistic
electron velocities, equation 11-4 becomes independent of
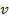 and reduces to7
and reduces to7 Equation
11-8 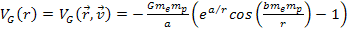
It is important to
realize that if the velocity of the electron remains relativistic
throughout its entire journey, the scattering angle would be
relatively small, and the scattering of the electron by the nucleon
would not be highly inelastic (for example, see the trajectory of the
electron in figure 11-3b, indicated in black). On the other extreme,
in cases of deep inelastic scattering at the limit where the energy
lost by the electron
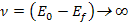 and
and
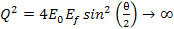 ,
the velocity of the electron in the vicinity of the point of impact
(or the point of closest approach), denoted ,
the velocity of the electron in the vicinity of the point of impact
(or the point of closest approach), denoted
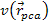 ,
must become negligible, thus ,
must become negligible, thus
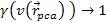 (see the electron trajectories in figure 11-3b, indicated in blue and
green).8
Due to their importance, events that provide extremely high values
of
(see the electron trajectories in figure 11-3b, indicated in blue and
green).8
Due to their importance, events that provide extremely high values
of
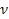 and
and
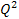 will be classified as Ďhigh-loss deep inelastic events.í
will be classified as Ďhigh-loss deep inelastic events.í
The
maxima and minima of the electronís potential energy can be
derived via
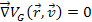 .
At non-relativistic velocities (which is the case in the immediate
vicinity of the electronís point of closest approach .
At non-relativistic velocities (which is the case in the immediate
vicinity of the electronís point of closest approach
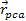 during a high-loss DIS event),
during a high-loss DIS event),
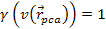 and the potential energy minima and maxima occur only when
and the potential energy minima and maxima occur only when
Equation
11-9a 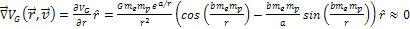
Therefore, at the
maxima or minima,
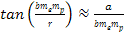 ,
or ,
or
Equation
11-9b 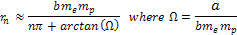
At distances where
the velocity of the electron is relativistic, the distortion of
spacetime may introduce
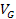 dependency on
dependency on
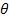 through the velocity terms, and may modify the dependency of the
potential energy
through the velocity terms, and may modify the dependency of the
potential energy
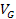 on the parametric distance
on the parametric distance
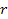 as well. As the velocity has no component along the inclination
angle,
as well. As the velocity has no component along the inclination
angle,
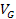 does not depend on
does not depend on
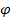 ,
and therefore ,
and therefore
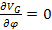 .
At distances .
At distances
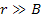 ,
the dependency of ,
the dependency of
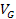 on the azimuth angle
on the azimuth angle
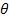 becomes insignificant, leading to approximately
becomes insignificant, leading to approximately
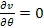 and
and
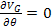 .
Therefore, at .
Therefore, at
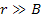 , ,
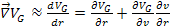 . However, at the maxima or minima of the potential energy,
. However, at the maxima or minima of the potential energy,
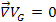 ,
and the force and acceleration must be equal to zero. Zero
acceleration leads to ,
and the force and acceleration must be equal to zero. Zero
acceleration leads to
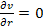 ,
resulting in ,
resulting in
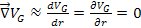 .
Consequently, the maxima or minima of .
Consequently, the maxima or minima of
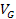 at parametric distances of
at parametric distances of
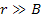 ,
where the velocity of the electron is relativistic, comply
approximately with ,
where the velocity of the electron is relativistic, comply
approximately with Equation
11-10a 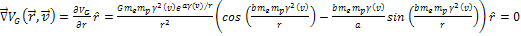
Therefore, at the
maxima or minima,
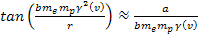 ,
or ,
or Equation
11-10b 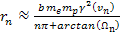
where
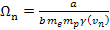 for the case of
for the case of
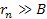 .
Note that at non-relativistic velocities, equations 11-10a and b
reduce to equations 10-9a and 10-9b respectively. Similarly, in the
case where .
Note that at non-relativistic velocities, equations 11-10a and b
reduce to equations 10-9a and 10-9b respectively. Similarly, in the
case where
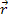 is perpendicular to the relativistic velocity of the electron,
is perpendicular to the relativistic velocity of the electron,
Equation
11-11 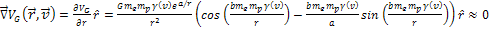
Therefore, in the
case where
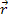 is perpendicular to the relativistic velocity of the electron,
is perpendicular to the relativistic velocity of the electron,
maxima or minima
occur when 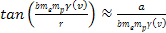
where
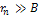 and
and
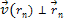 ,
or ,
or
Equation
11-12 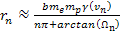
where
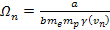 .
Note, however, that at distances less than or of the order of the
electronís impact parameter .
Note, however, that at distances less than or of the order of the
electronís impact parameter
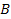 ,
the azimuth angle ,
the azimuth angle
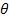 starts to vary substantially along the trajectory of the electron.
Consequently, at these small distances, equations 11-10 to 11-12 are
not entirely accurate for relativistic electron velocities, while
11-9a and 11-9b remain accurate at non-relativistic velocities.
starts to vary substantially along the trajectory of the electron.
Consequently, at these small distances, equations 11-10 to 11-12 are
not entirely accurate for relativistic electron velocities, while
11-9a and 11-9b remain accurate at non-relativistic velocities.
Section XI-1-2:
The Effect of Quantum Mechanics on DIS
Before
diving deeper into a UG analysis of deep inelastic scattering, it is
important to determine the highest level of precision that can be
achieved in calculating how close the electron came to the nucleon.
The natural tendency is to assume that the quantum uncertainty
principle restricts the level of precision of this distance. This is
the case, according to quantum mechanics, when the forces acting
between the particles are Newtonís gravitational force and/or
the electromagnetic force. However, this is not the case for the
exponential UG force. As
discussed above, the velocity of the probing electron of a high-loss
deep inelastic event (an event where
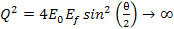 and
and
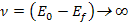 )
should become non-relativistic )
should become non-relativistic
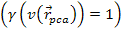 at the point of closest approach
at the point of closest approach
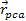 .
Given a high-loss DIS event, .
Given a high-loss DIS event,
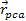 is located between the
is located between the
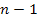 minimum and the
minimum and the
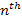 maximum of the most external zone indexed
maximum of the most external zone indexed
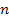 with potential energy maximum higher than the local overall energy of
the electron. The UG potential energy of the electron at the
with potential energy maximum higher than the local overall energy of
the electron. The UG potential energy of the electron at the
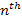 maximum can therefore be calculated by substituting equation 11-9b in
equation 11-8, providing
maximum can therefore be calculated by substituting equation 11-9b in
equation 11-8, providing Equation
11-1-1 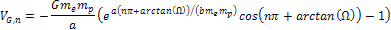
Given the high level
of energy required for deep inelastic scattering, the term
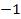 is negligible relative to the exponent, thus
is negligible relative to the exponent, thus Equation
11-1-2 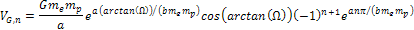
or
Equation
11-1-3a 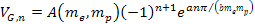
where
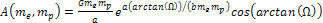 .
Maxima occur when the integer .
Maxima occur when the integer
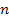 is odd, thus
is odd, thus
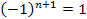 .
Therefore, the potential energy at the nearest maximum is
approximately given by .
Therefore, the potential energy at the nearest maximum is
approximately given by Equation
11-1-3b 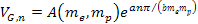
In the case of a
neutron, the electromagnetic interaction between the probing
electron and the neutron is zero. In the case of a proton, the
electromagnetic potential energy at the point of closest approach is
given approximately by the Coulomb equation at the nearest maximum
indexed
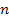 , ,
Equation
11-4 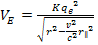
which
can be reduced to
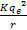 at non-relativistic electron velocities.
at non-relativistic electron velocities.
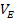 is a monotonic function of the parametric distance
is a monotonic function of the parametric distance
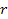 and does not have any maxima or minima. Consequently, the value of
and does not have any maxima or minima. Consequently, the value of
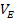 at the
at the
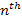 maximum or minimum of the UG potential energy
maximum or minimum of the UG potential energy
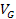 in the case of a non-relativistic electron velocity is given by
in the case of a non-relativistic electron velocity is given by
Equation
11-1-5 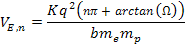
The uncertainty
principle restricts the certainty of simultaneously measuring the
electronís momentum and position via the inequality
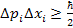 , where
, where
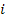 denotes the coordinates of
denotes the coordinates of
 , ,
 or
or
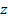 .
The uncertainty of the location of the electron .
The uncertainty of the location of the electron
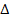 can
be approximated by can
be approximated by
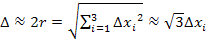 ,
or ,
or
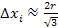 .
A similar calculation will yield .
A similar calculation will yield
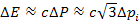 .
Therefore, the amount of kinetic energy required by the uncertainty
principle is given by .
Therefore, the amount of kinetic energy required by the uncertainty
principle is given by
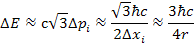
At the maxima and
minima of
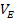 , , Equation
11-1-6 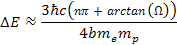
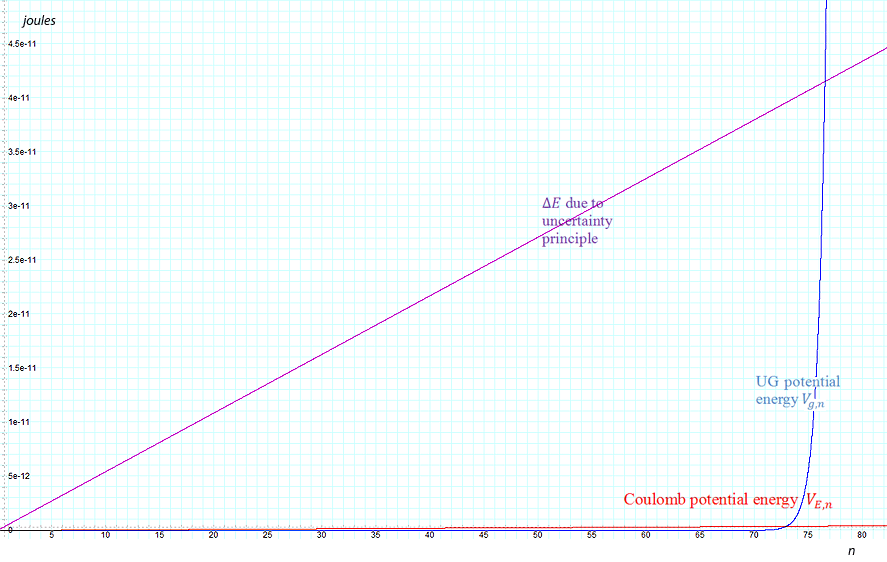
In figure 11-2 the
absolute value of the UG gravitational potential energy of the
electron
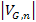 of equation 11-1-2 is displayed in blue, the absolute value of the
electromagnetic potential of the electron
of equation 11-1-2 is displayed in blue, the absolute value of the
electromagnetic potential of the electron
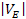 of equation 11-1-5 is displayed in red, and the absolute value of the
uncertainty of the amount of energy due to the uncertainty principle
of equation 11-1-5 is displayed in red, and the absolute value of the
uncertainty of the amount of energy due to the uncertainty principle
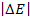 of equation 11-1-6 is provided in violet, as functions of the zonal
index
of equation 11-1-6 is provided in violet, as functions of the zonal
index
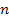 .9 .9
Figure
11-2
As demonstrated in
the figure, below
 the UG force is virtually zero, and is thus negligible relative to
the Coulomb force in the case where the interacting nucleon is a
proton.10
Moreover, throughout the range of distances associated with the
maxima and minima
the UG force is virtually zero, and is thus negligible relative to
the Coulomb force in the case where the interacting nucleon is a
proton.10
Moreover, throughout the range of distances associated with the
maxima and minima
 to
to
 ,
the uncertainty principle forces the energies to become so high that
any effort to accurately localize the electron in relation to the
nucleon is doomed to fail. However, due to the rapid exponential
growth of the UG interaction, the UG potential energy dominates over
the Coulomb interaction at ,
the uncertainty principle forces the energies to become so high that
any effort to accurately localize the electron in relation to the
nucleon is doomed to fail. However, due to the rapid exponential
growth of the UG interaction, the UG potential energy dominates over
the Coulomb interaction at
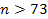 ,
and over the kinetic energy associated with the uncertainty principle
at ,
and over the kinetic energy associated with the uncertainty principle
at
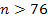 ,
which is roughly associated with energy levels above ,
which is roughly associated with energy levels above
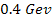 .
At energies higher than or of the order of .
At energies higher than or of the order of
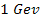 (for
(for
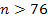 ),
quantum effects become negligible and the scattering can be localized
and viewed using classical physics methodology, thus making it
possible to locate the zone of closest approach in spite of the
uncertainty principle.11
Consequently, classical (non-quantum) methodology should provide a
reasonable approximation and will be used here for the analysis of
high-energy DIS events. ),
quantum effects become negligible and the scattering can be localized
and viewed using classical physics methodology, thus making it
possible to locate the zone of closest approach in spite of the
uncertainty principle.11
Consequently, classical (non-quantum) methodology should provide a
reasonable approximation and will be used here for the analysis of
high-energy DIS events.
Section XI-2-1:
The Effect of Special Relativity on the Range of the UG
Interaction
According
to equation 11-8 for the non-relativistic case
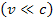 ,
the strength of the UG interaction between two nucleons, or between a
nucleon and an electron at a distance of ,
the strength of the UG interaction between two nucleons, or between a
nucleon and an electron at a distance of
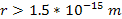 is negligible. Therefore, the effective range of the UG force on the
nuclear scale, for the case of non-relativistic electrons, is less
than
is negligible. Therefore, the effective range of the UG force on the
nuclear scale, for the case of non-relativistic electrons, is less
than
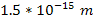 .
Consequently, a non-relativistic electron of an impact parameter of .
Consequently, a non-relativistic electron of an impact parameter of
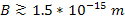 would demonstrate exclusively an electromagnetic interaction with a
proton, and virtually no interaction with a neutron. Under these
conditions, the interaction is too weak to create substantial
inelastic scattering. According to equation 2-1-1 and 2-1-2, at
non-relativistic velocities the UG interaction is comprised of a
central force that is independent of the speed of the electron
relative to the nucleon. However, as shown in equations 11-4, 11-6
and 11-7, at relativistic velocities the UG potential energy is
indirectly dependent on the electronís velocity due to
relativistic spacetime distortions and due to relativistic
massĖenergy equivalence. Therefore, at parametric distances
where a low-velocity electron is anticipated to remain unaffected by
its UG interaction with the nucleon, a relativistic electron may be
significantly influenced. Hence, the effective range of the UG
interaction may depend heavily on the relative velocity of the
electron.
would demonstrate exclusively an electromagnetic interaction with a
proton, and virtually no interaction with a neutron. Under these
conditions, the interaction is too weak to create substantial
inelastic scattering. According to equation 2-1-1 and 2-1-2, at
non-relativistic velocities the UG interaction is comprised of a
central force that is independent of the speed of the electron
relative to the nucleon. However, as shown in equations 11-4, 11-6
and 11-7, at relativistic velocities the UG potential energy is
indirectly dependent on the electronís velocity due to
relativistic spacetime distortions and due to relativistic
massĖenergy equivalence. Therefore, at parametric distances
where a low-velocity electron is anticipated to remain unaffected by
its UG interaction with the nucleon, a relativistic electron may be
significantly influenced. Hence, the effective range of the UG
interaction may depend heavily on the relative velocity of the
electron. Consider an
electron moving toward a nucleon with a kinetic energy of
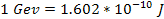 at a sufficiently large distance that the overall potential energy of
the electron is negligible.12
The Lorentz factor
at a sufficiently large distance that the overall potential energy of
the electron is negligible.12
The Lorentz factor
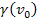 of the electron before the impact with the nucleon is therefore given
by
of the electron before the impact with the nucleon is therefore given
by Equation
11-2-1 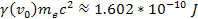 ,
or ,
or
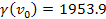 (or approximately
(or approximately
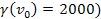
In
the case of highly relativistic electrons, the effect of the
electromagnetic interaction on the value of the Lorentz factor
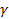 is relatively small, even for the case of interaction with a proton.
According to equation 11-5, at distances of
is relatively small, even for the case of interaction with a proton.
According to equation 11-5, at distances of
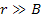 the velocity of the electron is virtually parallel to the
the velocity of the electron is virtually parallel to the
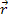 vector. Therefore, the distance between the electron and the proton
measured in the rest frame of the proton is given by
vector. Therefore, the distance between the electron and the proton
measured in the rest frame of the proton is given by
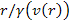 .13
According to equation 11-6, the distance .13
According to equation 11-6, the distance
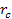 at which the UG interaction is about equal to the electromagnetic
interaction is given by
at which the UG interaction is about equal to the electromagnetic
interaction is given by Equation
11-2-2a 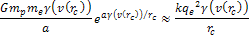
or Equation
11-2-2b 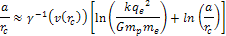
The equation may be
solved for
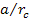 by either a titration technique, or via graphical calculator. For
the case of a non-relativistic electron (
by either a titration technique, or via graphical calculator. For
the case of a non-relativistic electron (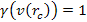 ),
the solution of equation 11-2-2b provides ),
the solution of equation 11-2-2b provides
Equation
11-2-2c 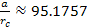 or
or
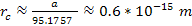
Therefore, at
distances of less than
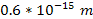 ,
the UG interaction between a proton and a non-relativistic electron
(relative to the proton) becomes stronger than the electromagnetic
interaction between them, yet becomes weaker than their
electromagnetic interaction at distances greater than ,
the UG interaction between a proton and a non-relativistic electron
(relative to the proton) becomes stronger than the electromagnetic
interaction between them, yet becomes weaker than their
electromagnetic interaction at distances greater than
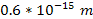 .
The same calculation shows that the range of the UG dominance is
extended by a factor of about 2,172 to .
The same calculation shows that the range of the UG dominance is
extended by a factor of about 2,172 to
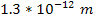 in the case of a relativistic electron, where
in the case of a relativistic electron, where
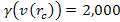 . .
Section XI-2-2:
DIS and the Relativistic Effect of the Folding and
Unfolding of the Particlesí Zonal Structure
In
high-energy head on collisions, a large amount of energy is converted
to potential energy by the electron as it encounters the point of
closest approach with the nucleon. During this process, the momentum
and the velocity of the electron relative to the particle
acceleratorís frame of reference are drastically reduced. To
preserve the overall momentum, the nucleonís momentum, and
therefore velocity, must increase significantly. However, since the
nucleon is strongly bonded to other nucleons within the atomic
nucleus, and the atom itself is bonded to other atoms or molecules, a
substantial portion of the transferred energy and momentum are
dispersed to the surrounding nucleons and molecules. These losses of
energy and momentum, as well as additional loss of energy and
momentum in the form of radiation, result in an inelastic scattering,
where the final energy of the electron (as viewed in either the
reference frame of the particle accelerator or of the nucleon)
reduces significantly. The amount of change in the energy and
momentum of the electron depends strongly on its initial energy and
momentum, and on its impact parameter. The explosive growth of the
exponential term of equation 11-4 as a function of
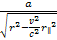 at distances of
at distances of
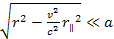 ,
as well as the sharp increase in the frequency of the oscillations of
the cosine term as ,
as well as the sharp increase in the frequency of the oscillations of
the cosine term as
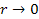 ,
cause the trajectories of the probing electrons to behave in a
chaotic manner. This behavior appears to be random, as a minute
difference in an electronís initial impact parameter or
velocity may result in drastically different scattering angles, as
well as in a different final momentum and energy. Therefore,
although the overall magnitude of the electromagnetic interaction in
high-energy deep inelastic scattering is very small compared with the
UG interaction, the electromagnetic effect may be significant in such
a chaotic system, where a tiny perturbation may result in an entirely
different trajectory. Consequently, regardless of the fact that the
initial energy and momentum of all of the electrons in the beam are
virtually identical, the trajectories of different electrons may vary
considerably. Thus, the point of closest
approach between different electrons, and their amount of
energy and momentum at these points, may vary
substantially. In experiments using particle accelerators
the velocities of the probing electrons
within a beam are all virtually equal. Therefore, the most
influential factor in determining the characteristics of the
scattering event is the impact parameter ,
cause the trajectories of the probing electrons to behave in a
chaotic manner. This behavior appears to be random, as a minute
difference in an electronís initial impact parameter or
velocity may result in drastically different scattering angles, as
well as in a different final momentum and energy. Therefore,
although the overall magnitude of the electromagnetic interaction in
high-energy deep inelastic scattering is very small compared with the
UG interaction, the electromagnetic effect may be significant in such
a chaotic system, where a tiny perturbation may result in an entirely
different trajectory. Consequently, regardless of the fact that the
initial energy and momentum of all of the electrons in the beam are
virtually identical, the trajectories of different electrons may vary
considerably. Thus, the point of closest
approach between different electrons, and their amount of
energy and momentum at these points, may vary
substantially. In experiments using particle accelerators
the velocities of the probing electrons
within a beam are all virtually equal. Therefore, the most
influential factor in determining the characteristics of the
scattering event is the impact parameter 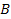 of the electron, and to a lesser degree,
whether the nucleon is a proton or a neutron.
of the electron, and to a lesser degree,
whether the nucleon is a proton or a neutron. In cases where the
impact parameter of the electron is sufficiently small, the electron
will approach the first impenetrable maximum barrier, where the
electronís potential energy at its peak exceeds the overall
energy of the electron. This outer maximum is expected to have an
odd integer index, denoted as the
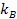 maximum. As the overall energy of the electron
is insufficient to penetrate the
maximum. As the overall energy of the electron
is insufficient to penetrate the
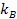 barrier, the electron will either be deflected to the side or
scattered backward by the barrier, in either case demonstrating a
large scattering angle and a substantial loss of energy. In
high-energy DIS collisions, the rate of reduction of the UG amplitude
as a function of an increasing parametric distance
barrier, the electron will either be deflected to the side or
scattered backward by the barrier, in either case demonstrating a
large scattering angle and a substantial loss of energy. In
high-energy DIS collisions, the rate of reduction of the UG amplitude
as a function of an increasing parametric distance
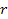 is high, and the slopes of the barrier at high zonal indices are
extremely steep. Consequently, the electronís energy must have
been greater than the maxima of most of the preceding zonal maxima
encountered prior to the point of closest approach, and the
electronís trajectory should have been minimally affected by
the majority of these preceding zones. Therefore, the electron will
be scattered by the
is high, and the slopes of the barrier at high zonal indices are
extremely steep. Consequently, the electronís energy must have
been greater than the maxima of most of the preceding zonal maxima
encountered prior to the point of closest approach, and the
electronís trajectory should have been minimally affected by
the majority of these preceding zones. Therefore, the electron will
be scattered by the
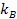 maximum zone in the same manner as it would be scattered by a hard
object of the same approximate shape as the contour of the
maximum zone in the same manner as it would be scattered by a hard
object of the same approximate shape as the contour of the
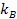 zone barrier, where the electronís kinetic energy is equal to
zero.
zone barrier, where the electronís kinetic energy is equal to
zero.
The
UG zonal structure generated by the interaction between the nucleon
and the electron consists of an infinite series of concentric
barriers around the nucleon, where the height and density of the
barriers approach infinity as
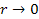 .
At non-relativistic velocities, these concentric barriers are
spherical and their distance from the nucleon is independent of the
electronís velocity. However, in the case of relativistic
electron velocities (relative to the nucleon), the shape of the
barriers begins to resemble a series of elongated ellipses, where
their major axes are aligned perpendicular to the velocity of the
electron. The heights and locations of these barriers, which are
fixed in the case of non-relativistic electron velocities, become
highly dependent on the speed of the electron at relativistic
electron velocities. .
At non-relativistic velocities, these concentric barriers are
spherical and their distance from the nucleon is independent of the
electronís velocity. However, in the case of relativistic
electron velocities (relative to the nucleon), the shape of the
barriers begins to resemble a series of elongated ellipses, where
their major axes are aligned perpendicular to the velocity of the
electron. The heights and locations of these barriers, which are
fixed in the case of non-relativistic electron velocities, become
highly dependent on the speed of the electron at relativistic
electron velocities.
According
to equation 11-5, at parametric distances
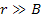 , ,
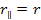 and
and
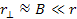 .
Therefore, the potential energy of the electron is given by equation
11-6, and the coordinates of the potential energy maxima (at odd .
Therefore, the potential energy of the electron is given by equation
11-6, and the coordinates of the potential energy maxima (at odd
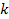 )
and minima (at even )
and minima (at even
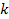 )
are given by 11-10b, or )
are given by 11-10b, or
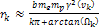 ,
where ,
where
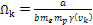 .
For a high-loss deep inelastic scattering event with a large
deflection angle to occur, the electronís potential energy at
the barrier maximum must match or exceed its overall energy at the
point of impact.14
The equations may be simplified by defining the function .
For a high-loss deep inelastic scattering event with a large
deflection angle to occur, the electronís potential energy at
the barrier maximum must match or exceed its overall energy at the
point of impact.14
The equations may be simplified by defining the function
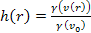 .
Since the lowest possible value for the Lorentz factor is .
Since the lowest possible value for the Lorentz factor is
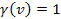 , ,
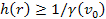 ,
and as the electron is expected to lose energy in a DIS event, ,
and as the electron is expected to lose energy in a DIS event,
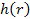 is typically less than
is typically less than
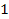 .
Denote .
Denote
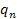 as the electric charge of the nucleon and define
as the electric charge of the nucleon and define
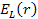 as the amount of energy lost by the electron by the time it arrived
at the parametric distance
as the amount of energy lost by the electron by the time it arrived
at the parametric distance
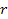 (when viewed in the rest frame of the nucleon).15
Using equation 11-6 for the UG potential energy, the overall energy
of the electron at any given parametric distance
(when viewed in the rest frame of the nucleon).15
Using equation 11-6 for the UG potential energy, the overall energy
of the electron at any given parametric distance
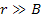 along its trajectory is given by
along its trajectory is given by Equation
11-2-4 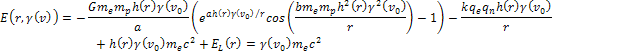
Where, the small
contribution of the particlesí spin is neglected.
At
DIS events, the UG maxima must be located at sufficiently short
distances, where the Coulomb term
 is negligible relative to the UG potential energy. Furthermore, at
such high energies the
is negligible relative to the UG potential energy. Furthermore, at
such high energies the
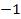 term within the parentheses is insignificant compared with the large
exponent term required for DIS and can be dropped.
term within the parentheses is insignificant compared with the large
exponent term required for DIS and can be dropped.
In cases where the energy of the electron on impact is just short of
being equal to its potential energy at the
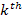 zonal maximum, as viewed in the rest frame of the nucleon, we can
substitute
zonal maximum, as viewed in the rest frame of the nucleon, we can
substitute
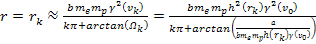 (where (where
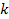 is an odd positive integer) in equation 11-2-4 to provide
is an odd positive integer) in equation 11-2-4 to provide Equation
11-2-5 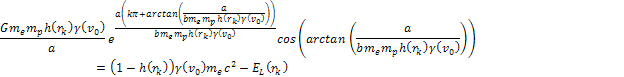
Multiplying both
sides by
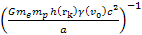 and then taking the log of both sides of the equation yields
and then taking the log of both sides of the equation yields Equation
11-2-6 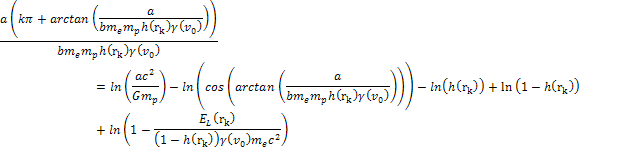
The
point of closest approach, denoted as
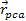 ,
generally occurs in the case of DIS somewhere within the ,
generally occurs in the case of DIS somewhere within the
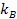 zone, but is assumed for the moment to occur very close to the
zone, but is assumed for the moment to occur very close to the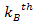 zonal maximum. Therefore, at this point in space and time,
zonal maximum. Therefore, at this point in space and time,
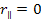 and
and
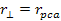 .
Consequently, .
Consequently,
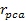 provides the actual distance between the electron and the nucleon, as
viewed in the rest frame of the nucleon. In the general case, the
electronís velocity
provides the actual distance between the electron and the nucleon, as
viewed in the rest frame of the nucleon. In the general case, the
electronís velocity
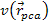 may be substantial, or even relativistic, and the resultant electron
scattering would not be highly inelastic. However, as discussed, for
a DIS event to occur where
may be substantial, or even relativistic, and the resultant electron
scattering would not be highly inelastic. However, as discussed, for
a DIS event to occur where
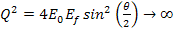 and
and
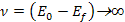 ,
the electron should become non-relativistic at the point of closest
approach ,
the electron should become non-relativistic at the point of closest
approach
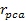 ,
with ,
with
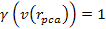 and
and
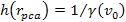 .
Therefore, .
Therefore,
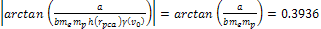 , ,
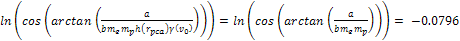 ,
and ,
and
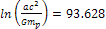 . .
As almost all of the energy of the electron is delivered to the
nucleon, while a significant portion of the nucleonís energy
dissipates into the network of surrounding nucleons, atoms and
molecules, the electronís loss of energy
 must be substantial. The energy loss
must be substantial. The energy loss
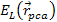 may cause the electron to stop its forward motion toward the nuclei
earlier, at a more external repulsive zone, and may consequently
lower the value of
may cause the electron to stop its forward motion toward the nuclei
earlier, at a more external repulsive zone, and may consequently
lower the value of
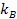 .
Substituting the above equalities in equation 11-2-6 yields .
Substituting the above equalities in equation 11-2-6 yields
Equation
11-2-7 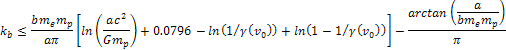
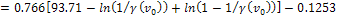
For example, provided that
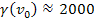 ,
the first maximum contour at which the potential energy of the
electron exceeds its initial overall energy is indexed ,
the first maximum contour at which the potential energy of the
electron exceeds its initial overall energy is indexed
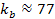 .
Note that energy losses may reduce .
Note that energy losses may reduce
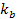 to an odd
to an odd
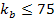 .
Intuition would suggest that as the electron was stopped by the .
Intuition would suggest that as the electron was stopped by the
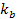 maximum, it should have passed through all minima and maxima of
maximum, it should have passed through all minima and maxima of
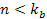 ,
and could not have reached any of the minima and maxima of index ,
and could not have reached any of the minima and maxima of index
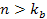 .
This will not be shown to be the case, however. While the electron
indeed had to pass all minima and maxima of .
This will not be shown to be the case, however. While the electron
indeed had to pass all minima and maxima of
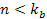 ,
it will be shown that the electron also had to pass maxima and minima
between ,
it will be shown that the electron also had to pass maxima and minima
between
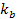 and
and
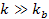 . .
At
parametric distances
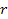 ,
where the potential energy of the electron is still small relative to
its overall energy, ,
where the potential energy of the electron is still small relative to
its overall energy,
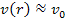 ;
hence ;
hence
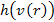 is still approximately
is still approximately
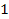 .
Therefore, no substantial energy loss has yet occurred, and .
Therefore, no substantial energy loss has yet occurred, and
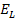 is negligible, leading to
is negligible, leading to
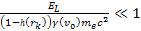 .
As .
As
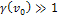 , ,
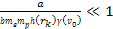 ,
and consequently, ,
and consequently,
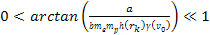 .
Following equation 11-2-6, .
Following equation 11-2-6, Equation
11-2-8 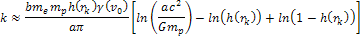
For
the example of
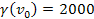 ,
at the point where ,
at the point where
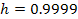 or
or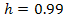 ,
the calculated index ,
the calculated index
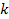 of the last encountered maximum is given by
of the last encountered maximum is given by
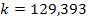 and
and
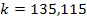 respectively, which are obviously much larger than the index of
respectively, which are obviously much larger than the index of
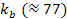 . .
Therefore,
before being stopped by the nucleon at the
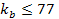 maximum,
the electron managed to pass substantially more than maximum,
the electron managed to pass substantially more than
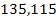 zones. The question arises as to how it is possible that an
electron in motion towards a nucleon, after successfully passing
through
zones. The question arises as to how it is possible that an
electron in motion towards a nucleon, after successfully passing
through
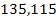 zones, ended up being stopped by a maximum barrier of an index as low
as
zones, ended up being stopped by a maximum barrier of an index as low
as
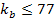 .
After all, the electron could not have reached the .
After all, the electron could not have reached the
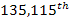 zone without first passing through all of the
zone without first passing through all of the
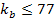 maxima. Additionally, the electronís potential energy at the
maxima. Additionally, the electronís potential energy at the
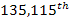 maximum should be substantially higher than its potential energy at
the
maximum should be substantially higher than its potential energy at
the
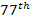 maximum. Therefore, it seems odd that the electron could be stopped
by a low energy maximum barrier after having passed a substantially
higher energy barrier earlier.
maximum. Therefore, it seems odd that the electron could be stopped
by a low energy maximum barrier after having passed a substantially
higher energy barrier earlier.
The
amplitude ratio between any two successive maxima (or minima) of
indices
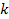 and
and
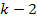 can be calculated by substituting
can be calculated by substituting
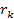 and
and
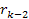 of equation 11-10bin equation 11-6. As long as
the overall energy of the electron is substantially greater than the
local potential energy maxima
of equation 11-10bin equation 11-6. As long as
the overall energy of the electron is substantially greater than the
local potential energy maxima
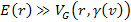 ,
or as long as the electronís velocity is non-relativistic
(therefore, ,
or as long as the electronís velocity is non-relativistic
(therefore,
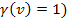 , ,
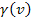 changes only slightly between two successive maxima, and
changes only slightly between two successive maxima, and
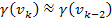 .
Therefore, provided that at high-energy collisions .
Therefore, provided that at high-energy collisions
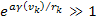 ,
the ratio of two successive maxima or minima peaks is given by ,
the ratio of two successive maxima or minima peaks is given by Equation
11-2-9 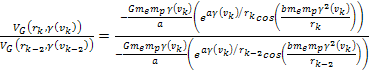
or Equation
11-2-10 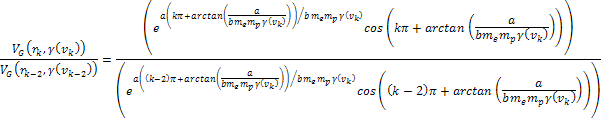
or
Equation
11-2-11
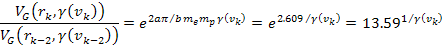
With the example
used above, where
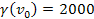 ,
the ratio in regions where ,
the ratio in regions where
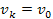 is given by
is given by
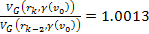 ,
compared with ,
compared with
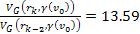 in regions where the electron moves at non-relativistic velocities.
The ratio of the electronís potential energy between the
in regions where the electron moves at non-relativistic velocities.
The ratio of the electronís potential energy between the
 maximum viewed by the electron at close to zero velocity (where
maximum viewed by the electron at close to zero velocity (where
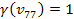 )
and the )
and the
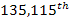 maximum viewed at
maximum viewed at
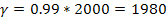 is given by
is given by
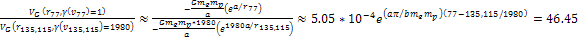 .
Therefore, the potential energy of the non-relativistic electron at
the time it was stopped by the .
Therefore, the potential energy of the non-relativistic electron at
the time it was stopped by the
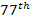 maximum substantially exceeds the potential energy of the
relativistic electron of
maximum substantially exceeds the potential energy of the
relativistic electron of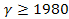 at the
at the
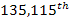 maximum. This explains how an electron can have a sufficient amount
of energy to pass the
maximum. This explains how an electron can have a sufficient amount
of energy to pass the
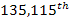 maximum barrier, yet not enough energy to pass the earlier
maximum barrier, yet not enough energy to pass the earlier
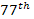 maximum
barrier. maximum
barrier.
However, the above
explanation does not account for how an electron that just passed the
zonal maximum indexed 135,115 can encounter the same
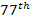 maximum for a second time while still moving toward the nucleon. The
explanation is as follows: While the parametric distance
maximum for a second time while still moving toward the nucleon. The
explanation is as follows: While the parametric distance
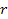 is reduced monotonically as the electron approaches the nucleon, the
apparent distance of the electron from the nucleon fluctuates wildly,
at times increasing and at times decreasing with the reduction of
is reduced monotonically as the electron approaches the nucleon, the
apparent distance of the electron from the nucleon fluctuates wildly,
at times increasing and at times decreasing with the reduction of
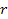 .
As it moves through the zones toward the nucleon, the electron
accelerates when approaching a potential energy minimum and
decelerates as it approaches a maximum. When approaching a potential
energy maximum, .
As it moves through the zones toward the nucleon, the electron
accelerates when approaching a potential energy minimum and
decelerates as it approaches a maximum. When approaching a potential
energy maximum,
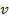 and
and
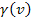 decrease. Consequently, the apparent distance between the electron
and the nucleon (as viewed by the nucleon), as well as the potential
energy ratio between two successive maxima (or minima), increases.
The opposite occurs when the electron approaches a minimum, in which
case
decrease. Consequently, the apparent distance between the electron
and the nucleon (as viewed by the nucleon), as well as the potential
energy ratio between two successive maxima (or minima), increases.
The opposite occurs when the electron approaches a minimum, in which
case
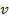 and
and
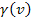 increase, and the apparent distance between the electron and the
nucleon (as viewed by the nucleon), as well as the potential energy
ratio between two successive maxima or minima, decreases. In effect,
as demonstrated by figures 11-1a and 11-1b, the entire zonal pattern
folds in when the velocity of the electron is decreased, causing the
patternís maxima and minima to move inward toward the nucleon.
Conversely, the pattern unfolds when the velocity of the electron is
increased, as the maxima and the minima move outward, away from the
nucleon. The speed of folding or unfolding depends on the rate of
change of the electronís Lorentz factor
increase, and the apparent distance between the electron and the
nucleon (as viewed by the nucleon), as well as the potential energy
ratio between two successive maxima or minima, decreases. In effect,
as demonstrated by figures 11-1a and 11-1b, the entire zonal pattern
folds in when the velocity of the electron is decreased, causing the
patternís maxima and minima to move inward toward the nucleon.
Conversely, the pattern unfolds when the velocity of the electron is
increased, as the maxima and the minima move outward, away from the
nucleon. The speed of folding or unfolding depends on the rate of
change of the electronís Lorentz factor
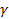 .
Early on, when the distance between the electron and the nucleon is
relatively large and the UG interaction is quite weak, the relative
velocity of the electron is about constant, and the rate of folding
and unfolding of the UG pattern is negligible. In a DIS event, as
the electron approaches the point of closest approach .
Early on, when the distance between the electron and the nucleon is
relatively large and the UG interaction is quite weak, the relative
velocity of the electron is about constant, and the rate of folding
and unfolding of the UG pattern is negligible. In a DIS event, as
the electron approaches the point of closest approach
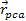 the maxima and the minima fluctuations become enormous, causing
related fluctuations in the value of
the maxima and the minima fluctuations become enormous, causing
related fluctuations in the value of
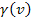 .
The size and rate of these fluctuations determine the speed and the
extent of the folding and unfolding of the pattern. The speeds of
the few folds preceding .
The size and rate of these fluctuations determine the speed and the
extent of the folding and unfolding of the pattern. The speeds of
the few folds preceding
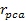 become large and may exceed the velocity of the electron. Hence,
some of the maxima already passed by the electron may fold or unfold
at a significantly faster rate than the speed of the electron, thus
overtaking the electron. It is therefore feasible, and even
expected, that in a DIS event the electron will encounter the same
maximum or minimum multiple times as it moves toward the nucleon.
become large and may exceed the velocity of the electron. Hence,
some of the maxima already passed by the electron may fold or unfold
at a significantly faster rate than the speed of the electron, thus
overtaking the electron. It is therefore feasible, and even
expected, that in a DIS event the electron will encounter the same
maximum or minimum multiple times as it moves toward the nucleon.
Section XI-3: The
Weak Fall-off of the DIS Cross Section
Prior to
calculating the approximate UG equation that describes the weak
fall-off of the DIS cross section, the underlying principle
responsible for this phenomenon can be demonstrated by the set of
figures 11-3a to 11-3d. Again, consider a high-loss DIS event at the
limit
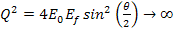 and
and
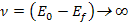 .
As discussed, in such an event the electron is scattered by the
outermost impenetrable zone indexed .
As discussed, in such an event the electron is scattered by the
outermost impenetrable zone indexed
 in the same manner as it would have been scattered by hard object.
However, the velocity of the electron becomes non-relativistic at the
point of impact. At non-relativistic velocities the zone structure
is spherically symmetric around the nucleon, and therefore depends on
the absolute value of the distance between the electron and the
nucleon,
in the same manner as it would have been scattered by hard object.
However, the velocity of the electron becomes non-relativistic at the
point of impact. At non-relativistic velocities the zone structure
is spherically symmetric around the nucleon, and therefore depends on
the absolute value of the distance between the electron and the
nucleon,
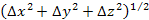 .
In addition, at non-relativistic speeds, when .
In addition, at non-relativistic speeds, when
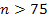 ,
the ratio between two successive potential energy maxima ,
the ratio between two successive potential energy maxima
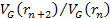 was shown by equation 11-2-11 to be approximately 13.59. The UG
potential energy waveform, indicated in violet in figure 11-3a, is
displayed as a function of the distance between the electron and the
nucleon along an arbitrary axis within the plane defined by the
electronís velocity vector and the distance vector between the
electron and the nucleon. The green concentric circles provide the
UG potential energy maxima contours within this plane. Note that
while the potential energy of successive maxima increases by a factor
of 13.59, the distance between them decreases proportionally to
was shown by equation 11-2-11 to be approximately 13.59. The UG
potential energy waveform, indicated in violet in figure 11-3a, is
displayed as a function of the distance between the electron and the
nucleon along an arbitrary axis within the plane defined by the
electronís velocity vector and the distance vector between the
electron and the nucleon. The green concentric circles provide the
UG potential energy maxima contours within this plane. Note that
while the potential energy of successive maxima increases by a factor
of 13.59, the distance between them decreases proportionally to
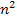 (see equation 2-1-16), where
(see equation 2-1-16), where
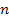 denotes the zonal index. Therefore, the UG slopes rapidly become
extremely steep.16
denotes the zonal index. Therefore, the UG slopes rapidly become
extremely steep.16
Figure
11-3a
The
overall energy of the electron illustrated in figure 11-3a is lower
than its potential energy at the
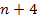 maximum. As the electron passes the
maximum. As the electron passes the
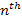 maximum, its overall energy is significantly larger than its
potential energy. Note that the electron retains most of its kinetic
energy; therefore only a small portion of its energy can be
transferred to the nucleon, and subsequently dispersed to nearby
nucleons, atoms and molecules. When the impact parameter of the
electron is larger than
maximum, its overall energy is significantly larger than its
potential energy. Note that the electron retains most of its kinetic
energy; therefore only a small portion of its energy can be
transferred to the nucleon, and subsequently dispersed to nearby
nucleons, atoms and molecules. When the impact parameter of the
electron is larger than
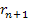 ,
the electron will not reach the maximum ,
the electron will not reach the maximum
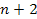 ,
and the amount of energy lost is relatively small. As a result, the
scattering event is only slightly inelastic. At an impact parameter
of ,
and the amount of energy lost is relatively small. As a result, the
scattering event is only slightly inelastic. At an impact parameter
of
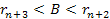 ,
the electron passes the higher potential energy maximum ,
the electron passes the higher potential energy maximum
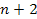 ,
and a greater portion of its kinetic energy is transferred directly
to the nucleon and indirectly to nearby nucleons, atoms and
molecules. Consequently, the scattering becomes increasingly
inelastic. At an impact parameter of ,
and a greater portion of its kinetic energy is transferred directly
to the nucleon and indirectly to nearby nucleons, atoms and
molecules. Consequently, the scattering becomes increasingly
inelastic. At an impact parameter of
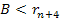 ,
the electron proceeds toward the ,
the electron proceeds toward the
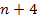 maximum. Since the electronís potential energy at this maximum
exceeds its overall energy, the electronís motion toward the
nucleon is halted as it reaches the point at which its potential
energy is equal its overall energy, at
maximum. Since the electronís potential energy at this maximum
exceeds its overall energy, the electronís motion toward the
nucleon is halted as it reaches the point at which its potential
energy is equal its overall energy, at
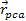 .17
As the electron does not have sufficient energy to continue to move
toward the nucleon, it is scattered in the same manner as it would
have been scattered by a hard object. Note that as the overall
energy of the electron at the impact point .17
As the electron does not have sufficient energy to continue to move
toward the nucleon, it is scattered in the same manner as it would
have been scattered by a hard object. Note that as the overall
energy of the electron at the impact point
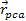 is equal to its potential energy, the velocity of the electron
relative to the nucleon is reduced to
is equal to its potential energy, the velocity of the electron
relative to the nucleon is reduced to
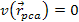 and its Lorentz factor is reduced to
and its Lorentz factor is reduced to
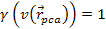 .
Since the electron becomes non-relativistic on impact, the UG zones
viewed in the particle acceleratorís frame of reference appear
spherically symmetric around the nucleon, and the hard scattering
object becomes a hard scattering sphere of radius .
Since the electron becomes non-relativistic on impact, the UG zones
viewed in the particle acceleratorís frame of reference appear
spherically symmetric around the nucleon, and the hard scattering
object becomes a hard scattering sphere of radius
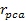 .
Hence, the high-loss DIS cross section becomes approximately equal
to .
Hence, the high-loss DIS cross section becomes approximately equal
to
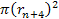 .
Note that the higher the energy of the probing electron, the smaller
the radius of the hard sphere becomes. .
Note that the higher the energy of the probing electron, the smaller
the radius of the hard sphere becomes.
Adhering to equation 11-2-11, in a DIS event, in regions where the
electron moves at non-relativistic velocities, the ratio between the
potential energy of an electron at two successive maxima
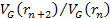 is equal to 13.59. Increasing the energy by a factor of
is equal to 13.59. Increasing the energy by a factor of
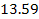 will therefore reduce the DIS cross section by a factor of
will therefore reduce the DIS cross section by a factor of 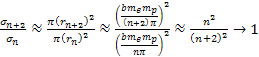 when
when
 .
Therefore, as .
Therefore, as
 increases, the DIS cross section is reduced. However, as
increases, the DIS cross section is reduced. However, as
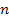 increases, the DIS cross section fall-off becomes exceedingly weak.
This phenomenon is demonstrated in figures 11-3b to 11-3d.
increases, the DIS cross section fall-off becomes exceedingly weak.
This phenomenon is demonstrated in figures 11-3b to 11-3d.
Figure
3-11b depicts three electrons with the same energy and different
impact parameters. The solid sphere indicates the impenetrable hard
sphere at the given level of energy, while the concentric circles
indicate the radii of the lower external maxima, which can be
penetrated as the potential energy of the electron at the maxima is
lower than the overall energy of the probing electrons. In
particular, the electronís potential energy at the surface of
the hard sphere is roughly given by
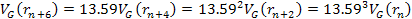 .
As displayed, the two electrons with the smaller impact parameters
(indicated by blue and green trajectories) hit the hard sphere and
are deflected by it. The electron with the largest impact parameter
(indicated by a black trajectory) passes near the nucleon without
colliding with the hard sphere, with only slight elastic deflection
by the lower indexed maxima and minima. Increasing the energy of the
electrons at the impact point ( .
As displayed, the two electrons with the smaller impact parameters
(indicated by blue and green trajectories) hit the hard sphere and
are deflected by it. The electron with the largest impact parameter
(indicated by a black trajectory) passes near the nucleon without
colliding with the hard sphere, with only slight elastic deflection
by the lower indexed maxima and minima. Increasing the energy of the
electrons at the impact point (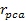 )
by a factor of )
by a factor of
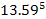 (to
(to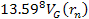 )
results in the reduction of the radius of the hard sphere to )
results in the reduction of the radius of the hard sphere to
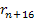 ,
where neither of the outer two electrons (black and green) collide
with the hard sphere.18 ,
where neither of the outer two electrons (black and green) collide
with the hard sphere.18
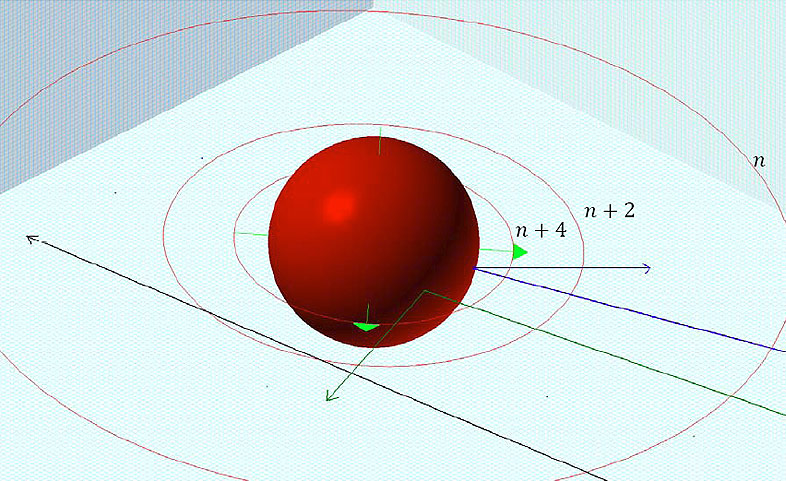
Figure
11-3b
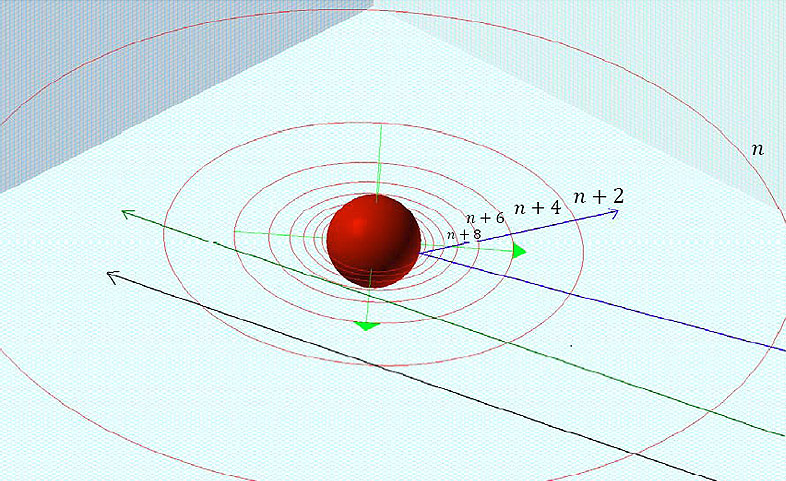
Figure
11-3c
In figure 11-3d the
impact energy of the electrons is further increased to about
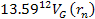 ,
resulting in the reduction of the radius of the hard sphere to ,
resulting in the reduction of the radius of the hard sphere to
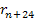 .
As shown in the figure, at high zonal indices the spherical maxima
become compacted together to the extent that increasing the
electronsí energy by a large factor results in little reduction
in the radii of the hard sphere, thus diminishing the rate of
reduction of the DIS cross section. .
As shown in the figure, at high zonal indices the spherical maxima
become compacted together to the extent that increasing the
electronsí energy by a large factor results in little reduction
in the radii of the hard sphere, thus diminishing the rate of
reduction of the DIS cross section.
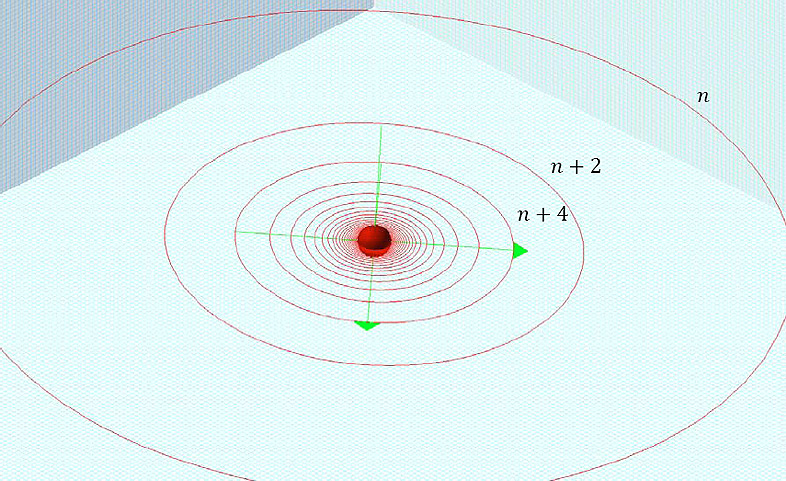
Figure
11-3d
Recall that close to
the impact point where the electronís velocity is no longer
relativistic, the effect of any zone
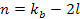 is smaller than the Ďhard sphereí effect of the
is smaller than the Ďhard sphereí effect of the
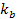 zone by a factor of at least
zone by a factor of at least
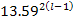 .
Thus, the effect of any zone .
Thus, the effect of any zone
 can be regarded as negligible.19
The trajectory of the electron can consequently be expected to be
deflected slightly by the maxima
can be regarded as negligible.19
The trajectory of the electron can consequently be expected to be
deflected slightly by the maxima
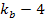 and
and
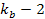 ,
and by the minima ,
and by the minima
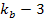 and
and
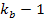 ,
before colliding with the hard sphere of a radius greater than ,
before colliding with the hard sphere of a radius greater than
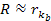 ,
where ,
where
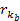 is the radius of the
is the radius of the
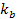 maximum contour. In summary, the highest DIS losses occur when the
electronís impact parameter is sufficiently small. As a
result, the electron is scattered as it would have been scattered by
a hard sphere, where the radius of the sphere
maximum contour. In summary, the highest DIS losses occur when the
electronís impact parameter is sufficiently small. As a
result, the electron is scattered as it would have been scattered by
a hard sphere, where the radius of the sphere is
equal to the distance of the point of closest approach is
equal to the distance of the point of closest approach
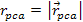 .
On the other hand, in cases where the impact parameter of the
electron is sufficiently large, the energy of the electron at the
point of closest approach (located at zone .
On the other hand, in cases where the impact parameter of the
electron is sufficiently large, the energy of the electron at the
point of closest approach (located at zone
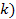 is higher than the maximum potential energy of zone
is higher than the maximum potential energy of zone
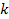 ,
thus ,
thus
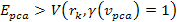 .
In this scenario, the electron will not collide with the hard sphere
and its velocity at the point of closest approach .
In this scenario, the electron will not collide with the hard sphere
and its velocity at the point of closest approach
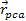 may still be relativistic. As the potential energy of the electron
reduces drastically with its distance from the nucleon, the
scattering becomes more elastic with an increased impact parameter.
may still be relativistic. As the potential energy of the electron
reduces drastically with its distance from the nucleon, the
scattering becomes more elastic with an increased impact parameter. Armed
with the above insights, the task at hand is to apply the same
principles and approximations for the development of a more precise
mathematical description of the weak fall-off of the DIS cross
section. At the point of closest approach
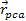 (viewed in the frame of reference of the particle accelerator), the
electronís velocity is either zero or perpendicular to
(viewed in the frame of reference of the particle accelerator), the
electronís velocity is either zero or perpendicular to
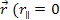 and
and
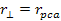 ). Therefore, the dynamics of the interaction at that point are
determined by equations 11-7 and 11-12. However, the electronís
energy at the point of closest approach
). Therefore, the dynamics of the interaction at that point are
determined by equations 11-7 and 11-12. However, the electronís
energy at the point of closest approach
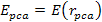 is not observable. To simplify the analysis, it is assumed that
is not observable. To simplify the analysis, it is assumed that
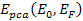 (or alternatively,
(or alternatively,
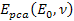 )
is a monotonic function of the electronís initial energy )
is a monotonic function of the electronís initial energy
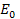 and
its final energy and
its final energy
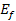 (or
(or
 ),
and that its behavior is consistent with20 ),
and that its behavior is consistent with20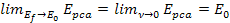 and, on average,
and, on average,
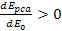 , ,
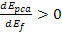 , ,
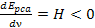 and
and
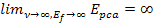 . . Expanding to the
first Taylor term, Equation
11-3-1 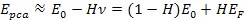
where
 is a constant.
is a constant.
The
index of the maximum of the zone containing
 will be denoted as
will be denoted as
 .
Consider the specific case where the parametric distance between the
nucleon and the point of closest approach is infinitesimally larger
than the radius of the .
Consider the specific case where the parametric distance between the
nucleon and the point of closest approach is infinitesimally larger
than the radius of the
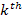 maximum contour,
maximum contour,
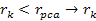 .
In this case, the potential energy of the electron in the nucleonís
frame of reference is given by .
In this case, the potential energy of the electron in the nucleonís
frame of reference is given by Equation
11-3-2 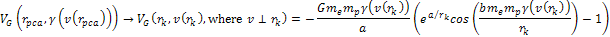
and the maxima occur
when
Equation
11-3-3 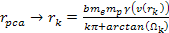
where
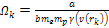 .
Substituting .
Substituting
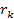 of equation 11-3-3 in equation 11-3-2 yields
of equation 11-3-3 in equation 11-3-2 yields
Equation
11-3-4 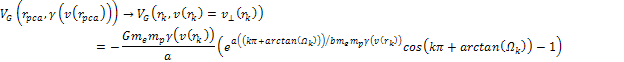
In cases of deep
inelastic scattering,
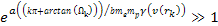 ,
and at a UG maximum, ,
and at a UG maximum,
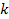 is an odd integer. Therefore,
is an odd integer. Therefore, Equation
11-3-5 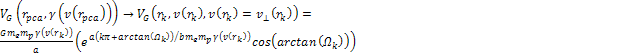
To simplify the
equation, define Equation
11-3-6 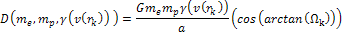
Therefore, equation
11-3-5 can be stated as
Equation
11-3-7 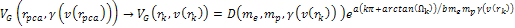
or, as of equations
11-3-3 and 11-3-7, Equation
11-3-8
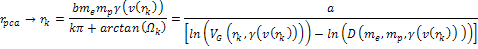
As
discussed above, when the kinetic energy of an electron is
substantial at
 ,
the influence of the nucleon on the electronís trajectory will
be relatively small, resulting in either an elastic scattering, or in
a weak inelastic scattering. For a substantial DIS event to take
place at the limits of ,
the influence of the nucleon on the electronís trajectory will
be relatively small, resulting in either an elastic scattering, or in
a weak inelastic scattering. For a substantial DIS event to take
place at the limits of
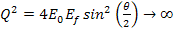 and
and
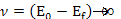 ,
the kinetic energy of the electron at ,
the kinetic energy of the electron at
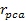 should be minimal, leading to
should be minimal, leading to
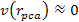 and
and
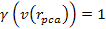 .
Therefore, in the case of a substantial DIS event, the parametric
(and apparent) distance of .
Therefore, in the case of a substantial DIS event, the parametric
(and apparent) distance of
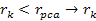 is given by
is given by Equation
11-3-9 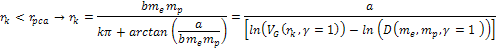
However, in the
usual case of a high-loss deep inelastic scattering event, the
electron will not collide directly with the peak of the
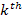 maximum, and will instead reach somewhere between
maximum, and will instead reach somewhere between
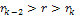 ,
where ,
where
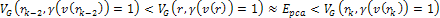 .21
As discussed above, for a substantial inelastic event to occur, the
electron must become non-relativistic on impact with .21
As discussed above, for a substantial inelastic event to occur, the
electron must become non-relativistic on impact with
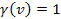 ,
somewhere within the ,
somewhere within the
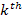 zone or at the tip of the
zone or at the tip of the
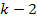 maximum. As
maximum. As
 may be anywhere within the range of
may be anywhere within the range of
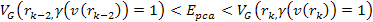 ,
the maximum potential energy at the ,
the maximum potential energy at the
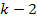 maximum is of the order of
maximum is of the order of
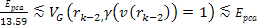 .
For the general maxima, the maximum potential energy at .
For the general maxima, the maximum potential energy at
 (at non-relativistic velocities) for an integer
(at non-relativistic velocities) for an integer
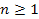 is given by
is given by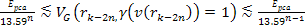 .
Therefore, in the case of deep inelastic scattering, only the
contributions of the preceding two or three maxima have a significant
effect. This is in agreement with experimental results, where 1 to 3
resonances are generally found in graphs of the double differential
cross section as function of energy (or vs. energy lost, .
Therefore, in the case of deep inelastic scattering, only the
contributions of the preceding two or three maxima have a significant
effect. This is in agreement with experimental results, where 1 to 3
resonances are generally found in graphs of the double differential
cross section as function of energy (or vs. energy lost,
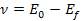 ).22 ).22
To calculate the approximate scattering cross section, we begin once
again with a high-loss DIS event where the impact energy of the
electron
 is slightly lower than
is slightly lower than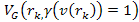 and its impact parameter
and its impact parameter
 is sufficiently small to produce hard sphere scattering. Therefore,
is sufficiently small to produce hard sphere scattering. Therefore,
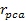 is slightly larger than
is slightly larger than
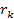 .
In this case, the .
In this case, the
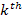 maximum contour cannot be penetrated by the probing electron, which
can only reach as deep as
maximum contour cannot be penetrated by the probing electron, which
can only reach as deep as
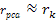 .
As the electronís velocity is already reduced to a
non-relativistic speed near the point of closest approach, the shape
of the .
As the electronís velocity is already reduced to a
non-relativistic speed near the point of closest approach, the shape
of the
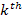 maximum is perceived by the electron to be spherically symmetric.
maximum is perceived by the electron to be spherically symmetric. As
discussed, in the case of a DIS event, the sharp steepness of the UG
exponent as a function of distance is so explosive near the point of
closest approach that the electronís course and direction of
motion remain largely unaffected by most of the UG maxima and minima
encountered, with the exception of the last few extremely narrow
zones between
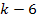 and
and
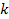 .
Therefore, the interaction distance and the interaction time
associated with DIS events, during which the electronís overall
energy and direction of motion have been significantly altered, are
extremely short. For this reason, although the electronís
direction of motion may have changed substantially, the effect of
this change on its impact parameter is minimal. Consequently, all
electrons with an impact parameter of .
Therefore, the interaction distance and the interaction time
associated with DIS events, during which the electronís overall
energy and direction of motion have been significantly altered, are
extremely short. For this reason, although the electronís
direction of motion may have changed substantially, the effect of
this change on its impact parameter is minimal. Consequently, all
electrons with an impact parameter of
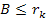 and an impact energy of
and an impact energy of
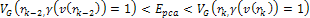 will scatter in the same manner as they would have been scattered by
a hard sphere of radius
will scatter in the same manner as they would have been scattered by
a hard sphere of radius
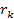 .
Electrons of the same range of energy, with impact parameters within
the range .
Electrons of the same range of energy, with impact parameters within
the range
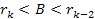 (as calculated for non-relativistic electrons) may undergo a weak
inelastic scattering, while electrons with impact parameters of
(as calculated for non-relativistic electrons) may undergo a weak
inelastic scattering, while electrons with impact parameters of
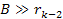 will undergo an elastic scattering, or will remain unaffected.
will undergo an elastic scattering, or will remain unaffected.
As
the cross section of a hard sphere of radius
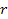 is given by
is given by
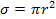 ,
the deep inelastic scattering event for the case of an impact energy ,
the deep inelastic scattering event for the case of an impact energy
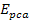 of just under
of just under
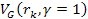 is given by
is given by Equation
11-3-10 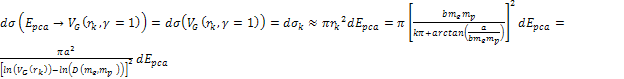
where
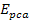 is less than yet almost equal to
is less than yet almost equal to
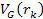 .2324
Similarly, if the energy is just under .2324
Similarly, if the energy is just under
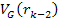 ,
where ,
where
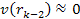 and
and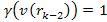 ), ), Equation
11-3-11 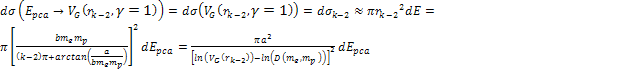
In a DIS event,
where
 , ,
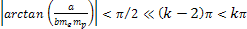 .
Therefore, .
Therefore, Equation
11-3-12 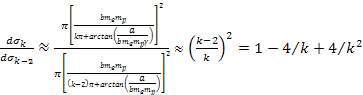
and consequently,
 .
Based on the above assumptions, the case of .
Based on the above assumptions, the case of
 leads to
leads to
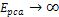 ,
and therefore to ,
and therefore to
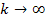 ,
and subsequently to ,
and subsequently to
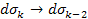 while
while
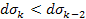 .
For the general case of an electron with an impact energy of .
For the general case of an electron with an impact energy of Equation
11-3-13 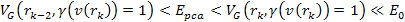
As
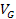 is a continuous function of
is a continuous function of
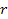 ,
there is always a radius ,
there is always a radius
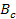 where
where
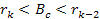 and
and
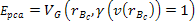 .
At an impact parameter .
At an impact parameter
 of less than
of less than
 ,
an electron with an impact energy of ,
an electron with an impact energy of
 will be scattered by the zone containing the
will be scattered by the zone containing the
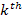 maximum in the same manner as it would have been scattered by a hard
sphere of radius
maximum in the same manner as it would have been scattered by a hard
sphere of radius
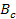 .
Therefore, at the limits of .
Therefore, at the limits of
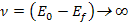 and
and
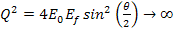 ,
the cross section of the DIS event must comply with ,
the cross section of the DIS event must comply with
Equation
11-3-14 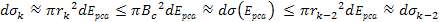
Therefore, according
to equations 11-3-11 and 11-3-12, for
 (or
(or
 ), ), Equation
11-3-15 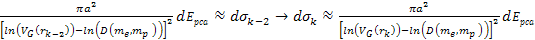
In order to comply
with equations 11-3-13, 11-3-14 and 11-3-15,
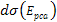 must comply with
must comply with Equation
11-3-16 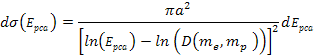
Consequently,
equation 11-3-16 provides a weak fall-off of
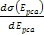 relative to the fall-off demonstrated by their elastic scattering,
which is proportional to
relative to the fall-off demonstrated by their elastic scattering,
which is proportional to
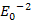 .
Note that this general behavior is consistent with
experimental observations. However, .
Note that this general behavior is consistent with
experimental observations. However,
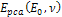 is not observable. Using the approximation given in equation 11-3-1
of
is not observable. Using the approximation given in equation 11-3-1
of
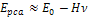 ,
where both ,
where both
 and and
 are observables, provides
are observables, provides
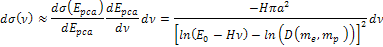
which also provides
a similar weak fall-off of
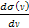 . .
Section XI-4:
Unified Gravitation and the Phenomenon of Bjorken
Scaling
Bjorken
scaling, demonstrated in figure 11-7, is the observed high-loss DIS
behavior where
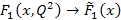 and
and
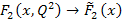 when
when
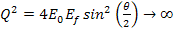 and
and
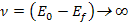 .
As discussed, high-loss DIS events adhering to .
As discussed, high-loss DIS events adhering to
 and
and
 occur when the electron is scattered by a hard sphere of radius
occur when the electron is scattered by a hard sphere of radius
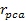 ,
where the velocity of the electron at the impact point of ,
where the velocity of the electron at the impact point of
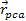 yields
yields
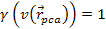 . .
From
the UG perspective, scaling becomes apparent when the UG force
dominates over the electromagnetic interaction and over the range of
energy affected by the uncertainty principle. Therefore, according
to section XI-1-2,
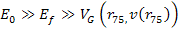 . .
The
physical underlying principle that leads to the observed Bjorken
scaling is demonstrated in figures 11-4a to 11-4e. The illustration
in figure 11-4a provides a tilted three dimensional image of the UG
potential energy. The illustration displays only three consecutive
maxima and one visible minimum out of an infinite set of maxima and
minima in the vicinity of the
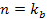 maximum.
maximum.
Figure 11-4b provides an illustration of the three dimensional
geometry of the deep inelastic scattering of the electron by the zone
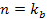 at
at
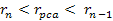 ,
where the blue area resides on the ,
where the blue area resides on the
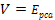 plane and
plane and
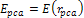 is the energy of the electron on impact (at
is the energy of the electron on impact (at
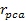 ).
The electronís energy is thus given by ).
The electronís energy is thus given by
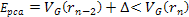 ,
where ,
where
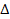 is small relative to
is small relative to
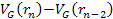 .
Consequently, the electron contains sufficient energy to pass the .
Consequently, the electron contains sufficient energy to pass the
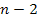 maximum, but not enough energy to penetrate the
maximum, but not enough energy to penetrate the
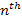 zone. The DIS cross section is equal to the circular area contained
within the outer circumference defined by the intersection of the
three dimensional UG surface with the blue
zone. The DIS cross section is equal to the circular area contained
within the outer circumference defined by the intersection of the
three dimensional UG surface with the blue
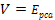 plane. At a higher electron energy, where
plane. At a higher electron energy, where
 is just below the maximum
is just below the maximum
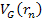 ,
as shown in figure 11-4c, the electron collides with the ,
as shown in figure 11-4c, the electron collides with the
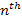 zone at a point slightly external to
zone at a point slightly external to
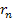 and the DIS cross section is slightly reduced. Note that as the
energy of the probing electrons changes continuously between
and the DIS cross section is slightly reduced. Note that as the
energy of the probing electrons changes continuously between
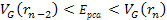 (approximately between the energy levels shown in figure 11-4b and
11-4c), the DIS cross section reduces continuously, and becomes
almost a linear function of the electronís energy level.
However, as the energy
(approximately between the energy levels shown in figure 11-4b and
11-4c), the DIS cross section reduces continuously, and becomes
almost a linear function of the electronís energy level.
However, as the energy
 becomes infinitesimally larger than
becomes infinitesimally larger than
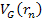 ,
the electron has sufficient energy to pass the ,
the electron has sufficient energy to pass the
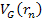 maximum. As the electron passes through
maximum. As the electron passes through
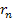 ,
its potential energy begins to fall drastically, and its velocity
increases as its potential energy is converted to kinetic energy.
After crossing the ,
its potential energy begins to fall drastically, and its velocity
increases as its potential energy is converted to kinetic energy.
After crossing the
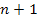 minimum, the electronís potential once again increases until
colliding with the zone containing the higher
minimum, the electronís potential once again increases until
colliding with the zone containing the higher
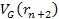 maximum at the point
maximum at the point
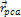 locatedbetween locatedbetween
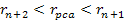 .
Consequently, the DIS cross section is reduced by more than .
Consequently, the DIS cross section is reduced by more than
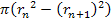 .
Therefore, as the energy of the electron in the vicinity of .
Therefore, as the energy of the electron in the vicinity of
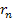 changes from being infinitesimally lower than the maximum
changes from being infinitesimally lower than the maximum
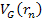 to infinitesimally higher than
to infinitesimally higher than
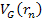 ,
the DIS cross section reduces abruptly, resulting in a discontinuity.
Such a transition is demonstrated in figure 11-4d. As the
electronís impact energy ,
the DIS cross section reduces abruptly, resulting in a discontinuity.
Such a transition is demonstrated in figure 11-4d. As the
electronís impact energy
 increases continuously between
increases continuously between
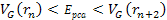 ,
the cross section will reduce continuously until the energy of the
electron becomes equal to ,
the cross section will reduce continuously until the energy of the
electron becomes equal to
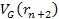 ,
where another discontinuity occurs. Hence, a discontinuity is
expected to occur when the energy of the electron at the point of
impact is equal to its potential energy at any given non-relativistic
UG maximum. ,
where another discontinuity occurs. Hence, a discontinuity is
expected to occur when the energy of the electron at the point of
impact is equal to its potential energy at any given non-relativistic
UG maximum. It
will be shown that the reduction of the DIS cross section can be
described to depend on two independent parameters. The first
parameter is the zone index that determines the electronís
impact energy levels
 at which discontinuities in the DIS cross section occur, as well as
the DIS cross section values on either side of each discontinuity.
The second parameter controls the approximately linear relationship
between the DIS cross section and the electronís energy at the
point of closest approach, within the range of energies lying between
two successive maxima. Note that at high zonal indices the slopes of
the UG potential energy become extremely steep (as demonstrated by
figure 11-3a), and the difference between the radii of two successive
maxima becomes negligible.
at which discontinuities in the DIS cross section occur, as well as
the DIS cross section values on either side of each discontinuity.
The second parameter controls the approximately linear relationship
between the DIS cross section and the electronís energy at the
point of closest approach, within the range of energies lying between
two successive maxima. Note that at high zonal indices the slopes of
the UG potential energy become extremely steep (as demonstrated by
figure 11-3a), and the difference between the radii of two successive
maxima becomes negligible.
At the energy range between the two maxima there is no notable change
in the cross section or in the radius of the hard sphere,
consequently creating an effect similar to Bjorken scaling, where the
cross section depends on a single parameter (in this case, the
potential energy maximum index). However, at low zonal indices the
slopes are less steep, and the difference between the radii of two
successive maxima is significant. Therefore, in the energy range
between the two maxima, the radius and cross section of the hard
sphere change notably as functions of the electronís impact
energy
 ,
thereby creating a visible break in scaling at low DIS energies. ,
thereby creating a visible break in scaling at low DIS energies. The above
principles can be applied for the development of a more detailed
mathematical description of these scaling behaviors. As stated,
Bjorken scaling is the observed high-loss DIS behavior where
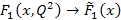 and
and
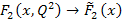 when
when
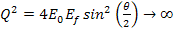 and
and
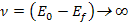 .
Bear in mind that these high-loss DIS events occur when the
electron is scattered by a hard sphere of radius .
Bear in mind that these high-loss DIS events occur when the
electron is scattered by a hard sphere of radius
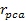 ,
where the velocity of the electron at the impact point of ,
where the velocity of the electron at the impact point of
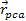 yields
yields
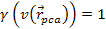 .
As .
As
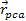 is located within the
is located within the
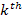 zone, the electronís velocity either reduces to a
non-relativistic velocity of
zone, the electronís velocity either reduces to a
non-relativistic velocity of
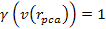 ,
or alternatively, the overall energy of ,
or alternatively, the overall energy of
the electron as it
passes through the
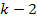 maximum is slightly higher than its potential energy with
maximum is slightly higher than its potential energy with
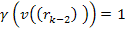 .25 .25 Consider
the case where the electronís impact energy
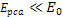 is just under the potential energy of
is just under the potential energy of
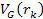 at the
at the
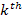 maximum. Therefore, an electron with a sufficiently large impact
parameter of
maximum. Therefore, an electron with a sufficiently large impact
parameter of
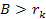 avoids collision with an impenetrable hard sphere, as demonstrated in
black in figure 11-3b, or in black and green in figure 11-3c.
avoids collision with an impenetrable hard sphere, as demonstrated in
black in figure 11-3b, or in black and green in figure 11-3c.
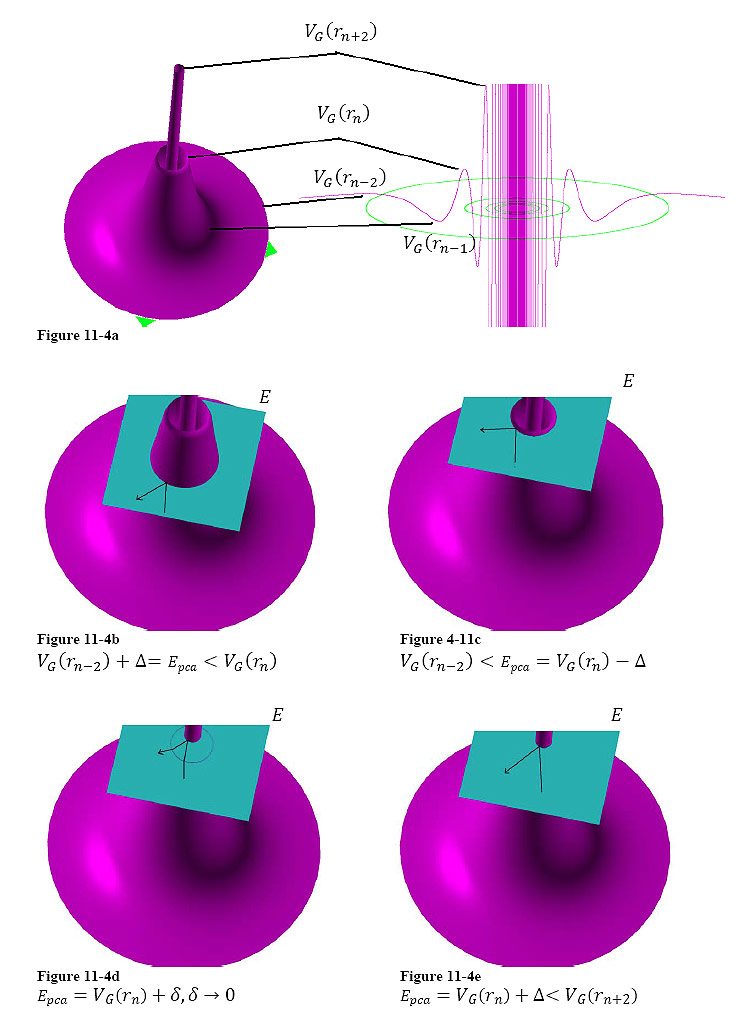
The
absolute value of the potential energy of the electron at any of the
remaining maxima and minima of
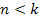 is significantly lower than
is significantly lower than
 .
Therefore, throughout its trajectory the electron retains a
substantial portion of its kinetic energy with .
Therefore, throughout its trajectory the electron retains a
substantial portion of its kinetic energy with
 significantly
larger than significantly
larger than
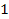 ,
and undergoes an elastic scattering with a relatively small
scattering angle. However, electrons with an impact parameter of ,
and undergoes an elastic scattering with a relatively small
scattering angle. However, electrons with an impact parameter of
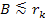 collide with an impenetrable hard sphere with a radius of
collide with an impenetrable hard sphere with a radius of
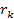 ,
as indicated in blue and green in figure 11-3b, or in blue in figure
11-3c. The potential energy of a non-relativistic electron at the
maximum indexed ,
as indicated in blue and green in figure 11-3b, or in blue in figure
11-3c. The potential energy of a non-relativistic electron at the
maximum indexed
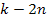 is equal to
is equal to
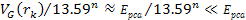 ,
where ,
where
 is an integer greater than zero. Hence, at least 92.6% of the
electronís energy at the
is an integer greater than zero. Hence, at least 92.6% of the
electronís energy at the
 maximum, and over 99% of the electronís energy at indices of
maximum, and over 99% of the electronís energy at indices of
 or lower must have been in the form of kinetic energy when
encountered by the electron. Consequently, the effect of the maxima
and minima of
or lower must have been in the form of kinetic energy when
encountered by the electron. Consequently, the effect of the maxima
and minima of
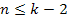 on the electronís path is relatively small. In addition, the
electron retains the majority of its velocity and kinetic energy when
it encounters any maximum of
on the electronís path is relatively small. In addition, the
electron retains the majority of its velocity and kinetic energy when
it encounters any maximum of
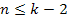 ,
while the velocity and kinetic energy of the electron may increase as
it encounters a minimum of ,
while the velocity and kinetic energy of the electron may increase as
it encounters a minimum of
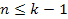 .26
Therefore, the electron is abruptly halted within the .26
Therefore, the electron is abruptly halted within the
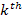 zone at about
zone at about
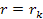 ,
leading to ,
leading to
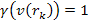 .
Consequently, the cross section .
Consequently, the cross section
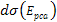 of electrons with an impact energy of
of electrons with an impact energy of
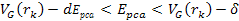 ,
where ,
where
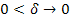 is equal to
is equal to Equation
11-4-1 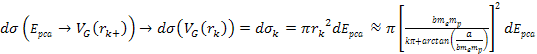
Bjorken scaling
should take place at distances where the effects of the
electromagnetic force and the uncertainty principle are negligible.
Note that the effects of the electromagnetic force and the
uncertainty principle were shown to become insignificant relative to
the UG force at
 .
Since .
Since
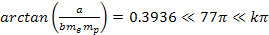 the following holds true:
the following holds true: Equation
11-4-2 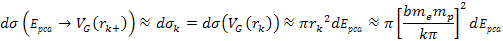
Similarly, for the
case where
 is just under the potential energy
is just under the potential energy
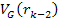 of the
of the
 maximum,
maximum, Equation
11-4-3 
Defining
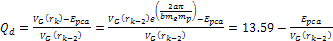 provides
provides Equation
11-4-4a 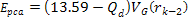
The impact energy
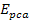 of the electron can therefore be fully defined by the variables
of the electron can therefore be fully defined by the variables
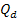 and
and
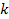 .
Hence, .
Hence,
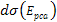 can be expressed as
can be expressed as
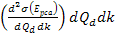 .27 .27 In
the case of an electron with an impact energy level falling anywhere
between its potential energy at the
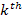 maximum and the
maximum and the
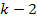 maximum,
maximum,
 is given by
is given by Equation
11-4-4b 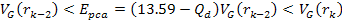
where Equation
11-4-4c 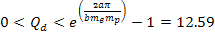
In such cases, an
electron with an initial impact parameter of
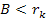 will have sufficient energy to penetrate the
will have sufficient energy to penetrate the
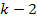 zone and to reach the
zone and to reach the
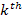 zone. As the
zone. As the
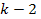 maximum and the
maximum and the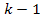 minimum are not negligible relative to
minimum are not negligible relative to
 ,
the electron will be deflected as it passes the ,
the electron will be deflected as it passes the
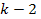 maximum, and again as it passes the
maximum, and again as it passes the
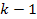 minimum. These deflections influence the energy and momentum of the
electron, and therefore its direction of propagation. However, as
the combined width of these zones is extremely narrow, the
deflections exert little effect on the actual location where the
electron encounters the
minimum. These deflections influence the energy and momentum of the
electron, and therefore its direction of propagation. However, as
the combined width of these zones is extremely narrow, the
deflections exert little effect on the actual location where the
electron encounters the
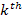 zone. Therefore, whether or not the given electron collides with a
hard sphere depends mainly on the electronís initial impact
parameter
zone. Therefore, whether or not the given electron collides with a
hard sphere depends mainly on the electronís initial impact
parameter
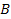 .28
With .28
With
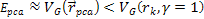 ,
the electron does not have sufficient energy to penetrate the ,
the electron does not have sufficient energy to penetrate the
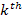 zone, and consequently, in the case of
zone, and consequently, in the case of
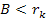 ,
the electron is deflected by a hard sphere and its forward motion
toward the nucleon is halted at the impact point. In the specific
case of a high-loss DIS event, where the energy lost by the electron ,
the electron is deflected by a hard sphere and its forward motion
toward the nucleon is halted at the impact point. In the specific
case of a high-loss DIS event, where the energy lost by the electron
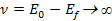 and
and
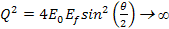 ,
the scattering angle approaches ,
the scattering angle approaches
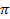 and the electronís relative velocity at the point of closest
approach (or impact point) becomes about zero, leading to
and the electronís relative velocity at the point of closest
approach (or impact point) becomes about zero, leading to
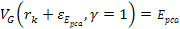 .
Note that it was taken into consideration that the rest mass of the
electron as well as its nearly diminished kinetic energy at the
impact point .
Note that it was taken into consideration that the rest mass of the
electron as well as its nearly diminished kinetic energy at the
impact point
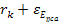 are negligible relative to the impact energy
are negligible relative to the impact energy
 .
Since the electron is scattered by a nearly hard sphere of radius .
Since the electron is scattered by a nearly hard sphere of radius
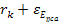 ,
its cross section is given by ,
its cross section is given by
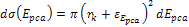 .
Consequently, the minimum value of .
Consequently, the minimum value of
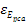 is at the limit
is at the limit
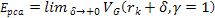 ,
and ,
and
 as the distance between the point of closest approach and the nucleon
converges toward
as the distance between the point of closest approach and the nucleon
converges toward
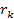 .
On the other hand, the maximal value of .
On the other hand, the maximal value of
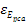 ,
denoted ,
denoted
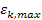 ,
is associated with the minimum energy ,
is associated with the minimum energy
 with which the electron can penetrate the
with which the electron can penetrate the
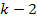 zone as it approaches and recedes from the impact point on its way to
the detector. This energy value is significantly more difficult to
calculate for several reasons. First, the velocity of the electron
as it encounters the
zone as it approaches and recedes from the impact point on its way to
the detector. This energy value is significantly more difficult to
calculate for several reasons. First, the velocity of the electron
as it encounters the
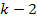 maximum is unknown, and may be relativistic, and consequently may
affect the height and the perceived location of the
maximum is unknown, and may be relativistic, and consequently may
affect the height and the perceived location of the
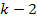 maximum. In addition, the amount of energy lost by the electron
during the time it spent between the distances of the
maximum. In addition, the amount of energy lost by the electron
during the time it spent between the distances of the
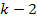 maximum and
maximum and
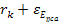 is substantial, thus the energy of the electron as it passes through
the
is substantial, thus the energy of the electron as it passes through
the
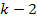 maximum is uncertain. However, it is clear that
maximum is uncertain. However, it is clear that
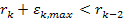 ,
where ,
where
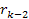 is the radius of the
is the radius of the
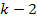 maximum, as perceived by a non-relativistic electron.
maximum, as perceived by a non-relativistic electron. In the case of an
electron with an impact energy of
 ,
where ,
where
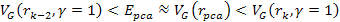 ,
and an impact parameter of ,
and an impact parameter of
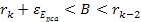 ,
the electron will escape the ,
the electron will escape the
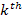 zone without colliding with its impenetrable hard sphere. The
electron will then re-enter zone
zone without colliding with its impenetrable hard sphere. The
electron will then re-enter zone
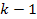 on its way toward the detector, while retaining a non-zero and
possibly relativistic velocity at the point of closest approach
on its way toward the detector, while retaining a non-zero and
possibly relativistic velocity at the point of closest approach
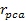 within the
within the
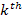 zone. At an impact parameter
zone. At an impact parameter
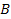 just above
just above
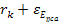 ,
the scattering may still be significantly inelastic, however, as the
value of ,
the scattering may still be significantly inelastic, however, as the
value of
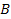 approaches
approaches
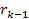 ,
the scattering becomes less inelastic. ,
the scattering becomes less inelastic.
Consequently,
DIS cross sections demonstrate discontinuity at energy levels that
match the potential energy of the zonal maxima. In the case of a
close encounter between the electron and the
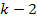 maximum, the cross section reduces abruptly from
maximum, the cross section reduces abruptly from
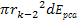 to
to
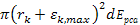 .
As the electronís impact energy .
As the electronís impact energy
 continues to increase between
continues to increase between
 and
and
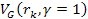 ,
the cross section decreases gradually toward ,
the cross section decreases gradually toward
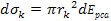 .
The next discontinuity occurs at the energy .
The next discontinuity occurs at the energy
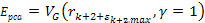 ,
where the cross section reduces abruptly from ,
where the cross section reduces abruptly from
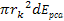 to
to
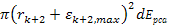 .
This pattern of discontinuities, or scaling gaps, depicted in
Figure 11-5 will be shown to occur, and to provide a scaling
phenomenon that is similar to Bjorken scaling. .
This pattern of discontinuities, or scaling gaps, depicted in
Figure 11-5 will be shown to occur, and to provide a scaling
phenomenon that is similar to Bjorken scaling. As
discussed, since
 is a continuous function of the parametric distance
is a continuous function of the parametric distance
 ,
for any ,
for any
 compliant with
compliant with
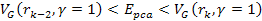 ,
there is a distance ,
there is a distance
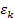 at which
at which
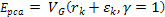 ,
where ,
where
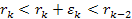 .
Therefore, .
Therefore,
Equation
11-4-5 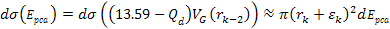
where the value of
 depends on the values of
depends on the values of
 and
and
 .
For a high-loss deep inelastic scattering to take place, the
potential energy at the point of closest approach must comply with .
For a high-loss deep inelastic scattering to take place, the
potential energy at the point of closest approach must comply with
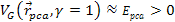 and
and
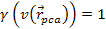 .
The zero crossing of the potential energy of a non-relativistic
electron preceding .
The zero crossing of the potential energy of a non-relativistic
electron preceding
 can be denoted as
can be denoted as
 .
Thus, .
Thus,
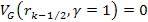 ,
where ,
where
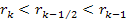 .
At the impact point .
At the impact point
 ,
where ,
where
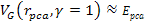 ,
the slope of the potential energy ,
the slope of the potential energy
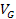 must be negative. Further note that
must be negative. Further note that
 must be positive for the electron to escape the nucleon and reach the
detector. Therefore, the range of distances between
must be positive for the electron to escape the nucleon and reach the
detector. Therefore, the range of distances between
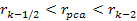 can be ruled out as possible distances for scattering by a hard
sphere. Consequently, the value of
can be ruled out as possible distances for scattering by a hard
sphere. Consequently, the value of
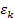 is restricted to the range of
is restricted to the range of
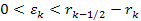 .
This creates a discontinuity in the cross section function, as the
cross section of .
This creates a discontinuity in the cross section function, as the
cross section of
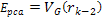 is given by
is given by
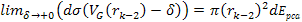 ,
while the DIS cross section of an infinitesimally higher impact
energy ,
while the DIS cross section of an infinitesimally higher impact
energy
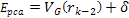 results in
results in
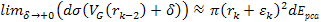 ,
where ,
where
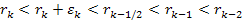 .
These discontinuities (or gaps), denoted as .
These discontinuities (or gaps), denoted as
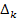 ,
are given by ,
are given by Equation
11-4-6 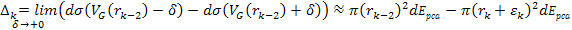
or Equation
11-4-7 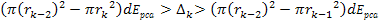
Recall
that the velocity of the electron
upon being scattered by the higher potential energy barrier is
non-relativistic. Hence, the above inequalities can also be
estimated for the non-relativistic electron, Equation
11-4-8 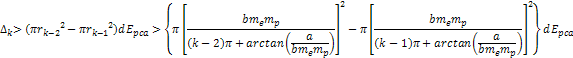
As
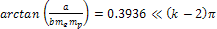 , , Equation
11-4-9 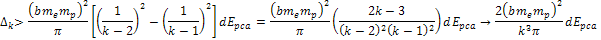
and
Equation
11-4-10 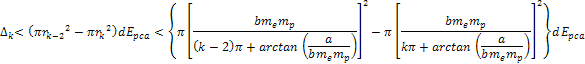
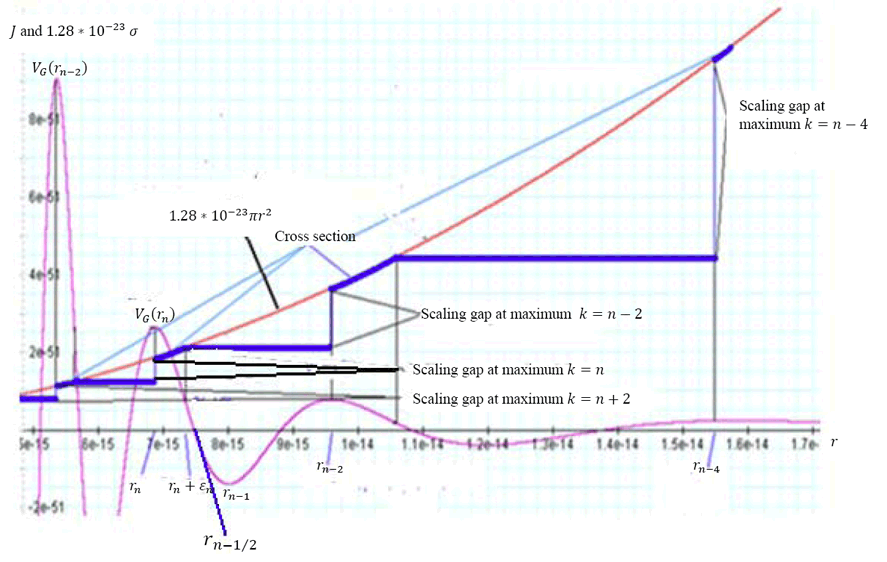
Figure 11-5: Provides
an illustration of the DIS cross section of
particles such as electrons by a nucleon (note
that for the purpose of clarity, the mass of the scattered particle
used in this example is slightly larger than mass of an electron,
allowing for the clear identification of more than three maxima in
the graph). The figure further includes the curve of 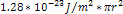 ,
which is proportional to the hard sphere cross section of a zone.
The multiplication factor is included in order to allow the hard
sphere cross section to be displayed in the same figure, along the
zone energies. Discontinuity in the cross section can be noted at
every maximum, creating cross section Ďscaling gapsí
between the zones and generating a phenomenon similar to the observed
Bjorken scaling. The degree of curvature of the
cross section between any two successive discontinuities becomes
increasingly insignificant as ,
which is proportional to the hard sphere cross section of a zone.
The multiplication factor is included in order to allow the hard
sphere cross section to be displayed in the same figure, along the
zone energies. Discontinuity in the cross section can be noted at
every maximum, creating cross section Ďscaling gapsí
between the zones and generating a phenomenon similar to the observed
Bjorken scaling. The degree of curvature of the
cross section between any two successive discontinuities becomes
increasingly insignificant as  and and
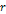 reduce, and as
reduce, and as 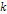 increases (where the zone maximum index, given by an odd integer
increases (where the zone maximum index, given by an odd integer 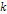 ,
is analogous to ,
is analogous to 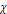 ,
where ,
where 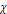 is the Bjorken scale variable). This increase in the cross section
curvature at low k indices (low
is the Bjorken scale variable). This increase in the cross section
curvature at low k indices (low 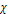 values)
explains the break in scaling at low values of values)
explains the break in scaling at low values of 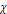 . .As
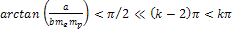 , ,
Equation
11-4-11 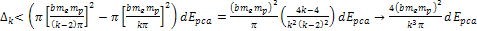 as as 
Therefore, the width
of the
 discontinuity in the cross section is consistent with
discontinuity in the cross section is consistent with
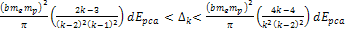 ,
which converges to ,
which converges to
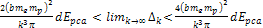 as
as
 . .
Consequently,
deep inelastic scattering results in a series of discontinuities that
resemble the behavior of Bjorken scaling. The next step is to
determine the behavior of the double differential cross section as a
function of
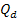 and the zonal index
and the zonal index
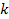 . . Knowledge
of the value of
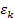 is required for the calculation of the cross section scaling pattern.
The approach taken here is to approximate
is required for the calculation of the cross section scaling pattern.
The approach taken here is to approximate
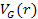 by a linear function lying between the potential energy of a
non-relativistic electron at the maximum
by a linear function lying between the potential energy of a
non-relativistic electron at the maximum
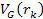 ,
located at ,
located at
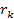 ,
and the preceding zero crossing ,
and the preceding zero crossing
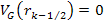 ,
located at ,
located at
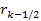 .
Note that the selection of the non-relativistic values of .
Note that the selection of the non-relativistic values of
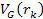 and
and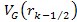 is driven by the realization that for a DIS event to occur, the
velocity of the electron at the impact location of
is driven by the realization that for a DIS event to occur, the
velocity of the electron at the impact location of
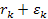 should be close to zero. The slope
should be close to zero. The slope
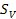 of this function is given by
of this function is given by Equation
11-4-12 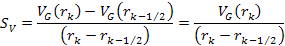
Therefore,
the distance
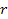 at which a particle with an impact energy of
at which a particle with an impact energy of
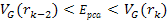 will encounter a potential energy equal to
will encounter a potential energy equal to
 is given approximately by is given approximately by Equation
11-4-13 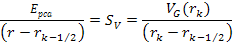
or Equation
11-4-14 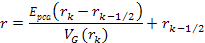
At a
minimum,
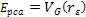 cannot be lower than
cannot be lower than
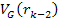 .
Otherwise, the electron would remain trapped between the .
Otherwise, the electron would remain trapped between the
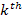 maximum and the
maximum and the
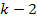 maximum, and would not reach the detector. Solving specifically for
the minimum at
maximum, and would not reach the detector. Solving specifically for
the minimum at
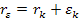 ,
where ,
where
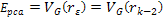 ,
provides ,
provides Equation
11-4-15 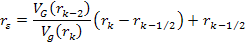
According to equation 11-8, non-relativistic
 zero crossings occur where
zero crossings occur where
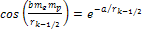 .
In a high-energy DIS experiment the UG exponent .
In a high-energy DIS experiment the UG exponent
 must be very large. Subsequently,
must be very large. Subsequently,
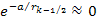 .
Thus, .
Thus,
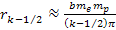 .
Defining .
Defining
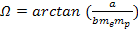 and using equations 11-4-15, 11-2-11 and 11-9b (with and using equations 11-4-15, 11-2-11 and 11-9b (with
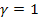 at
both at
both
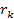 and
and
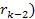 ,
as well as the above expression for ,
as well as the above expression for
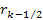 ,
yields ,
yields Equation
11-4-16 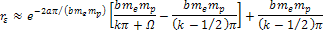
or Equation
11-4-17 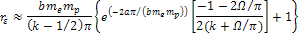
and Equation
11-4-18 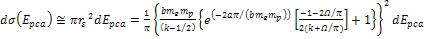 when when
 is just above
is just above 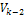
In
the general case, in which the electronís impact energy
 in the rest frame of the nucleon is within the range
in the rest frame of the nucleon is within the range
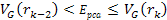 ,
the cross section ,
the cross section
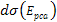 (using equation 11-4-14) is given approximately by
(using equation 11-4-14) is given approximately by Equation
11-4-19 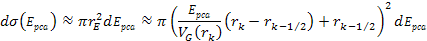
or Equation
11-4-20 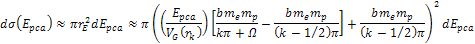
or Equation
11-4-21 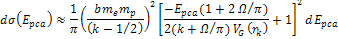
Substituting
equation 11-1-2, where
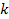 is an odd integer, into equation 11-4-21 yields
is an odd integer, into equation 11-4-21 yields Equation
11-4-22 
Under
the condition where
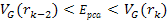 ,
equation 11-1-3b at the maxima ,
equation 11-1-3b at the maxima
 and
and
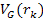 provides
provides Equation
11-4-23 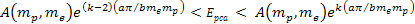
Substituting
equations 11-4-23 and 11-4-4a in equation 11-4-22 yields
Equation
11-4-24 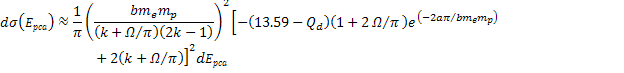
Substituting
the estimated values
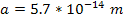 , ,
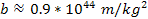 and the given masses of the electron and proton into equation
11-4-24, with the realization that at close to a
and the given masses of the electron and proton into equation
11-4-24, with the realization that at close to a
 scattering angle the velocity at the point of closest approach is
non-relativistic, results in
scattering angle the velocity at the point of closest approach is
non-relativistic, results in
Equation
11-4-25 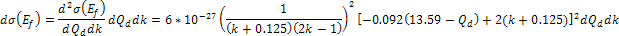
where
according to equation 11-4-4c,
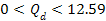 .
Figures 11-6a and 11-6b illustrate the resulting scaling behavior by
displaying the Ďhard sphereí cross section .
Figures 11-6a and 11-6b illustrate the resulting scaling behavior by
displaying the Ďhard sphereí cross section
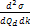 as a function of
as a function of
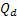 .
Each waveform is associated with the inelastic scattering produced
by electron collisions with a given .
Each waveform is associated with the inelastic scattering produced
by electron collisions with a given
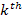 zone, where
zone, where
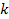 is an odd integer.
is an odd integer.
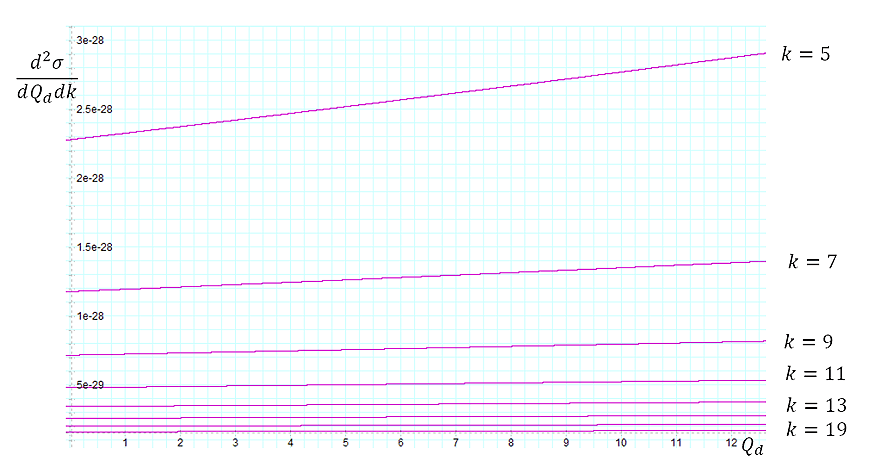 Figure
11-6a: Display of the
UG DISdouble
differential cross section scaling, calculated via equation 11-4-25,
due to repulsive zones above Figure
11-6a: Display of the
UG DISdouble
differential cross section scaling, calculated via equation 11-4-25,
due to repulsive zones above  .
Note that within the provided range of energies, where .
Note that within the provided range of energies, where  ,
the effect of the UG scaling may be masked by the much larger
electromagnetic interaction, as well as by the effect of the
uncertainty principle. Nevertheless, the figure is displayed in
order to effectively demonstrate the scaling break that occurs at
relatively low ,
the effect of the UG scaling may be masked by the much larger
electromagnetic interaction, as well as by the effect of the
uncertainty principle. Nevertheless, the figure is displayed in
order to effectively demonstrate the scaling break that occurs at
relatively low 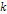 values.
values.
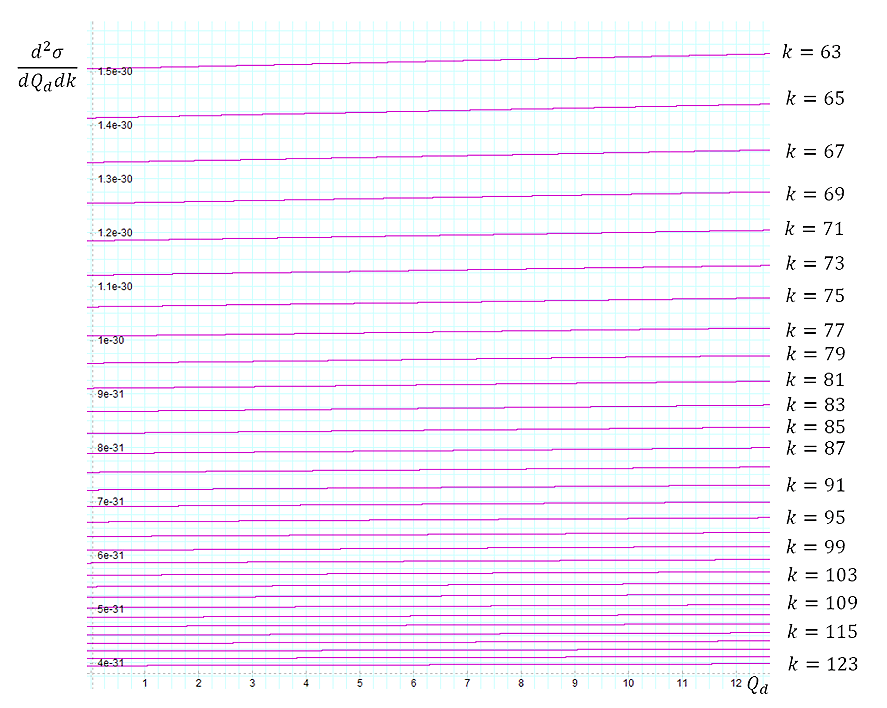 Figure
11-6b: Display of the
calculated double differential cross section of a UG deep inelastic
scattering in the range
between Figure
11-6b: Display of the
calculated double differential cross section of a UG deep inelastic
scattering in the range
between  and
and  .
Across most of this range of energy, the UG interaction dominates
over the effects of the electromagnetic interaction, and the
uncertainty principle. The displayed cross section provides clear
scaling properties, as well as a break in the scaling at low .
Across most of this range of energy, the UG interaction dominates
over the effects of the electromagnetic interaction, and the
uncertainty principle. The displayed cross section provides clear
scaling properties, as well as a break in the scaling at low  values. The scaling pattern in figures 11-6a and b bears a
resemblance to the observed Bjorken
scaling pattern of the form factor
values. The scaling pattern in figures 11-6a and b bears a
resemblance to the observed Bjorken
scaling pattern of the form factor 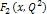 provided in Figure 11-7 within the range of
provided in Figure 11-7 within the range of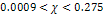 ,
where an odd ,
where an odd 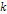 is analogous to the Bjorken variable
is analogous to the Bjorken variable 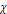 and the factor
and the factor 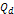 is analogous to
is analogous to 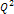 . .As
demonstrated in equation 11-4-25, and in figures 11-6a and 11-6b, the
dependency of the DIS double differential cross section on
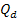 is relatively weak, and therefore provides a scaling pattern similar
to the observed Bjorken scaling. Similar to Bjorken scaling, the
calculated scaling of equation 11-4-25 displays a break in the
scaling at low values of
is relatively weak, and therefore provides a scaling pattern similar
to the observed Bjorken scaling. Similar to Bjorken scaling, the
calculated scaling of equation 11-4-25 displays a break in the
scaling at low values of
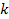 ,
in which the cross section ,
in which the cross section
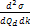 is increased with increasing is increased with increasing
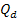 .
As anticipated, an increase in .
As anticipated, an increase in
 (signifying that the scattering becomes more inelastic) corresponds
with an increase in
(signifying that the scattering becomes more inelastic) corresponds
with an increase in
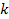 ,
while an increase in ,
while an increase in
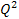 corresponds with an increase in
corresponds with an increase in
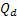 .29 .29 Using
equations 11-3-16 and 11-4-4a, the scaling and the break in the
scaling at low
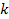 values are given by
values are given by Equation
11-4-26 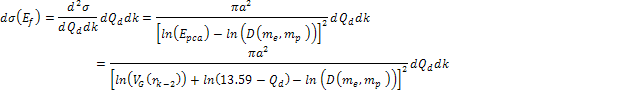
where 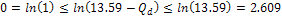 . . 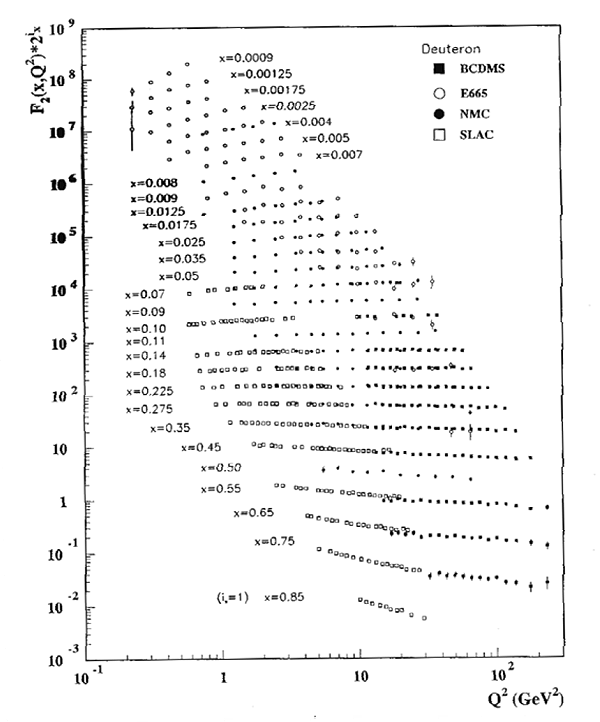
Figure
11-7: The deuteron
structure function  measured in electromagnetic scattering of electrons
(SLAC) and muons (BCDMS, E665, NMC) on a fixed target, shown as a
function of
measured in electromagnetic scattering of electrons
(SLAC) and muons (BCDMS, E665, NMC) on a fixed target, shown as a
function of  for bins of fixed
for bins of fixed 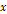 .
Statistical and systematic errors added in quadrature are shown.
For the purpose of plotting, .
Statistical and systematic errors added in quadrature are shown.
For the purpose of plotting, 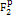 has been multiplied by
has been multiplied by  ,
where ,
where 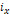 is the number of the
is the number of the 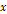 bin, ranging from
bin, ranging from 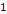 (
( )
to )
to  (
(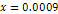 ).
References: H1-C. Adolff et al., Eur. Phys. J. C21, 33 (2001); C.
Adolff et al., Eur. Phys. J. hep-ex/0304003; ZEUS-S. Chekanov et al.,
Eur. Phys. J. C21,443 (2001); BCDMS-A.C. Benvenuti et al., Phys.
Lett. B223, 485 (1989); E665-M.R. Adams et al., Phys Rev. D54, 3006
(1996); NMC-M. Arneodo et al., Nucl. Phys. B483, 3 (97); SLAC-L.W.
Whitlow et. Al., Phys. Lett. B282, 475 (1992). (Source: ď16.
Structure FunctionsĒ by B. Foster, A.D. Martin and M.G.
Vincter, citation: W. M. Yao et al., Journal of Physics G 33, 1
(2006) available on the PDG WWW pages (URL: http;//pdg.1bl.gov/) July
2006.) ).
References: H1-C. Adolff et al., Eur. Phys. J. C21, 33 (2001); C.
Adolff et al., Eur. Phys. J. hep-ex/0304003; ZEUS-S. Chekanov et al.,
Eur. Phys. J. C21,443 (2001); BCDMS-A.C. Benvenuti et al., Phys.
Lett. B223, 485 (1989); E665-M.R. Adams et al., Phys Rev. D54, 3006
(1996); NMC-M. Arneodo et al., Nucl. Phys. B483, 3 (97); SLAC-L.W.
Whitlow et. Al., Phys. Lett. B282, 475 (1992). (Source: ď16.
Structure FunctionsĒ by B. Foster, A.D. Martin and M.G.
Vincter, citation: W. M. Yao et al., Journal of Physics G 33, 1
(2006) available on the PDG WWW pages (URL: http;//pdg.1bl.gov/) July
2006.)
Equation
11-4-26 demonstrates that when
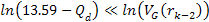 for odd
for odd
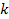 , ,
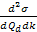 is almost independent of
is almost independent of
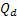 (thus resulting in the scaling phenomenon). At lower odd
(thus resulting in the scaling phenomenon). At lower odd
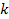 indices, where
indices, where
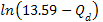 is
not negligible compared with is
not negligible compared with
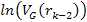 , ,
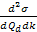 declines with decreasing declines with decreasing
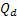 ,
generating the break in scaling observed for low ,
generating the break in scaling observed for low
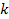 (or low
(or low
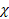 )
values. In either case, the DIS cross section fall-off with
decreasing )
values. In either case, the DIS cross section fall-off with
decreasing
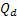 (or increasing
(or increasing
 and decreasing
and decreasing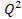 )
is significantly weaker than the elastic scattering (which falls off
proportionally to )
is significantly weaker than the elastic scattering (which falls off
proportionally to
 ).
As stated above, this weaker fall-off provided by the UG theory is
consistent with reported experimental data in the range of ).
As stated above, this weaker fall-off provided by the UG theory is
consistent with reported experimental data in the range of
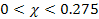 . .
1
at the Stanford Linear Accelerator Center (SLAC) 2
Note, however, that the UG theory does not necessarily contradict
the existence of quarks
as elementary constituents of hadrons.
3 The electrical charge is equal
to 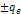 or
or 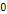 ,
where ,
where 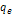 denotes the charge of a proton.
denotes the charge of a proton. 4
Note that this book does not deal with the weak force, which is
viewed by the standard model
as a separate force. 5
To calculate 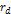 , ,
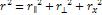 ,
where ,
where 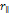 contracts to
contracts to 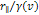 , ,
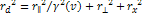 .
Thus, .
Thus, 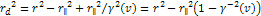 ,
or ,
or 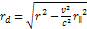 . . 6
Note that in the general case, the electronís
potential energy  depends on the vectors
depends on the vectors  and and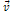 .
However, in cases where it is clear that either .
However, in cases where it is clear that either 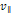 or
or 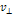 are relatively insignificant, the notation
are relatively insignificant, the notation 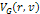 or
or 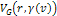 may be used. For example, see equations 11-6 for the case of
may be used. For example, see equations 11-6 for the case of  ,
or equation 11-7 for the case of ,
or equation 11-7 for the case of  ).
In cases of non-relativistic velocity, where ).
In cases of non-relativistic velocity, where  becomes independent of
becomes independent of 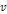 ,
the notations ,
the notations 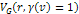 or
or 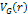 may be used.
may be used. 7 Note
that at 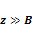 ,
or when ,
or when  is perpendicular to
is perpendicular to 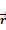 ,
the potential energy ,
the potential energy 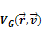 is reduced to depend on
is reduced to depend on  and
and  (or
(or 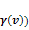 .
At shorter distances, where .
At shorter distances, where  approaches the impact parameter
approaches the impact parameter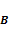 , ,
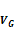 becomes dependent on
becomes dependent on  , ,
 and
and 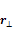 .
In the non-relativistic case, .
In the non-relativistic case, 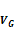 depends exclusively on
depends exclusively on  .
Therefore, the notations .
Therefore, the notations 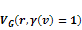 and
and 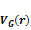 will be used interchangeably throughout this chapter.
will be used interchangeably throughout this chapter.8
The logic behind this statement is as follows: The initial energy 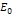 of the electrons is fixed
by the experimental setup.
of the electrons is fixed
by the experimental setup. 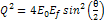 increases as
increases as 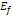 increases and as
increases and as 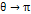 .
The energy loss of the scattered electron .
The energy loss of the scattered electron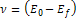 is not directly dependent on the scattering angle
is not directly dependent on the scattering angle 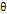 ,
but increases with decreasing ,
but increases with decreasing 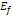 .
Thus, increasing .
Thus, increasing 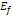 will increase
will increase 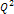 and decrease
and decrease 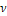 ,
and vice versa. Therefore, other than setting the highest possible
value of the electronsí
initial energy ,
and vice versa. Therefore, other than setting the highest possible
value of the electronsí
initial energy 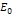 ,
high values of both ,
high values of both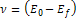 and
and 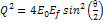 can be achieved when
can be achieved when  is within a specific range of energy values, and when the scattering
angle
is within a specific range of energy values, and when the scattering
angle  is as close as possible to
is as close as possible to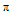 .
With this scattering geometry, the electron
and the nucleon nearly undergo a head on collision, where the
relative velocity of the electron
nearly reduces to zero at the point of closest approach .
With this scattering geometry, the electron
and the nucleon nearly undergo a head on collision, where the
relative velocity of the electron
nearly reduces to zero at the point of closest approach 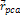 .
Hence, .
Hence, 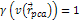 .
As will be discussed later on in the chapter, the electron
in such a case is effectively scattered by a hard sphere. .
As will be discussed later on in the chapter, the electron
in such a case is effectively scattered by a hard sphere. 9
Using equation 11-9b (or equation 11-12, where 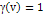 )
leads to )
leads to 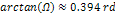 . . 10
Note that the distance between the electron
and the nucleon increases with decreasing  . . 11
Note that this analysis does not imply that the electromagnetic
interaction and the uncertainty principle are completely negligible
at 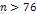 ,
as they may still bear some influence on the zero intersections of
the gravitational potential energy ,
as they may still bear some influence on the zero intersections of
the gravitational potential energy  .
In addition, the electromagnetic force
may pull the electron
closer to the nucleon, thereby reducing its impact parameter.
As previously noted, the impact parameter plays a crucial role in
determining the outcome of the DIS
event. .
In addition, the electromagnetic force
may pull the electron
closer to the nucleon, thereby reducing its impact parameter.
As previously noted, the impact parameter plays a crucial role in
determining the outcome of the DIS
event. 12
Note that the rest mass energy of the electron
(of about 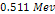 )
is relatively negligible. )
is relatively negligible. 13
Note that at DIS events
the nucleon demonstrates substantial acceleration. Consequently,
its rest frame can be inertial for only a brief period of time. 14 Note that in deep inelastic
scattering, the energy
associated with the electronís
rest mass is negligible relative to its overall energy and therefore
can be neglected. 15
As the nucleon is accelerated significantly during the DIS
event, its rest frame is not inertial, and consequently, the overall
energy and momentum of the system is not preserved. Therefore, 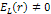 is possible. While this frame of reference is not inertial over the
entire period of the DIS
event, it can be viewed as an inertial frame
at any parametric distance
is possible. While this frame of reference is not inertial over the
entire period of the DIS
event, it can be viewed as an inertial frame
at any parametric distance 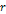 for a brief period of time. Therefore, equation 11-2-4 is valid.
for a brief period of time. Therefore, equation 11-2-4 is valid. 16 Note that lower mass values were
used for the figures in this chapter in order to view more maximum
and minimum peaks. 17
Note that the energy at the impact point 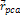 within the nucleonís frame of reference is not equal to the
initial energy of the electron.
This is due to energy losses endured, as well as to the fact that
the nucleonís frame of reference cannot remain inertial for a
sufficient amount of time, due to the acceleration of the nucleon.
within the nucleonís frame of reference is not equal to the
initial energy of the electron.
This is due to energy losses endured, as well as to the fact that
the nucleonís frame of reference cannot remain inertial for a
sufficient amount of time, due to the acceleration of the nucleon. 18
The index increase from
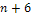 to
to
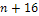 (by 10), rather than to
(by 10), rather than to
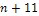 (by 5) reflects that there are five minima in addition to the five
maxima separating the radii of the two hard spheres.
(by 5) reflects that there are five minima in addition to the five
maxima separating the radii of the two hard spheres. 19
Note however, that as the velocity of the electron was higher and
may have been relativistic when passing through the previous
maximum, the ratio between two successive maxima may reduce to below
13.59.
20
Note that the nucleon is accelerated by the electron. Therefore, its
frame of reference can be regarded as an inertial frame for only a
brief period of time. Consequently, the law of conservation of
energy does not apply.
21The
reason for the assumption that 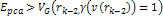 is that the electron had
to pass the
is that the electron had
to pass the 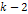 maximum just before impact with the
maximum just before impact with the  zone, and then had to pass the maximum again immediately after the
impact, on its way toward the
detector.
zone, and then had to pass the maximum again immediately after the
impact, on its way toward the
detector. 22
Note that there is also a split of the potential energy maxima due
to the slight difference in mass between the proton and the neutron,
which may impact the number of resonances. 23 In cases where 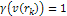 ,
the notations ,
the notations 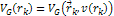 and
and 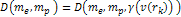 may be used.
may be used. 24
The DIS cross section can
be written as 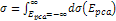 .
However, in the case of a negative .
However, in the case of a negative 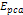 value, the electron would
remain trapped, and would never reach the detector. Therefore,
value, the electron would
remain trapped, and would never reach the detector. Therefore, 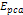 cannot be negative. In addition, as the electron
is extremely unlikely to gain energy during the scattering event,
cannot be negative. In addition, as the electron
is extremely unlikely to gain energy during the scattering event, 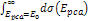 should be negligible. Therefore, the overall UG cross section can
be expressed as
should be negligible. Therefore, the overall UG cross section can
be expressed as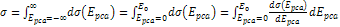 . . 25
In the non-quantum approach, the overall energy of the electron
must be somewhat above 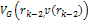 as it passes through this maximum, otherwise the electron
would not be able to enter and subsequently exit the
as it passes through this maximum, otherwise the electron
would not be able to enter and subsequently exit the  zone, which contains
zone, which contains 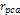 ,
on its way toward the detector. ,
on its way toward the detector. 26
At even  indices,
indices, 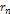 is a minimum and its potential energy is negative. Therefore, it is
possible that the velocity and the kinetic energy of the electron
as it encounters these minima may be larger than their initial
values.
is a minimum and its potential energy is negative. Therefore, it is
possible that the velocity and the kinetic energy of the electron
as it encounters these minima may be larger than their initial
values. 27 Note that the potential energy
maxima are odd integers, therefore 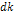 is not continuous, and instead changes in steps of two.
is not continuous, and instead changes in steps of two. 28
Note that the UG and the electromagnetic interactions are both
long-range forces. In proton-electron
scattering, at all distances greater than nuclear scale, the UG
contribution is negligible compared with the electromagnetic
contribution (by a factor of approximately 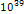 )
and can be neglected. However, at such distances the
electromagnetic force
reduces the impact parameter )
and can be neglected. However, at such distances the
electromagnetic force
reduces the impact parameter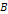 by pulling the electron
toward the proton. This may explain why the cross section of a
proton-electron DIS
is observed to be larger than the cross section of a
neutron-electron DIS
as the Bjorken scale
variable
by pulling the electron
toward the proton. This may explain why the cross section of a
proton-electron DIS
is observed to be larger than the cross section of a
neutron-electron DIS
as the Bjorken scale
variable 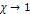 . . 29 Providing that experimental data
becomes available in this form (where the overall DIS
cross section is dependent on 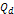 and on odd
and on odd 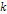 ,
rather than on ,
rather than on 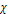 and and
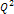 ),
the values of the UG constants ),
the values of the UG constants 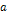 and
and 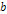 could be calculated with greater accuracy.
could be calculated with greater accuracy.
|



