Gravitational redshift is a well known phenomenon, first predicted by
Einsteinís relativity theories and then verified
experimentally. According to general relativity, the redshift of a
photon within the gravitational field of a non-rotating uncharged
spherically symmetric mass
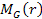 is viewed by a distant observer as
is viewed by a distant observer as Equation
10-1-1 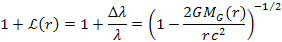
where the redshift
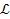 ,
and its equivalent velocity ,
and its equivalent velocity
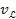 are defined as
are defined as
Equation
10-1-2
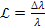 and
and
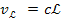
where
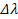 provides the difference between the radiation wavelength measured
at the inertial rest frame of the observer, denoted provides the difference between the radiation wavelength measured
at the inertial rest frame of the observer, denoted
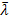 ,
and the wavelength of the same radiation line emitted by a ďfreeĒ
atom measured at the inertial rest frame of the emitting atom,
denoted ,
and the wavelength of the same radiation line emitted by a ďfreeĒ
atom measured at the inertial rest frame of the emitting atom,
denoted
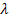 . .
Therefore, it is not surprising that the gravitational field of a
galaxy may influence the amount of redshift of its radiation.
However, it was not expected that the amount of redshift may show
periodicity. The first researcher to observe such periodicity was
William G. Tifft in the 1970s (Tifft, 1973).
Tifft reported that galaxies in the Coma Cluster show periodic
redshift, with periodicity of about
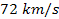 ,
followed by the later discovery of periodicity of about ,
followed by the later discovery of periodicity of about
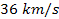 .
A similar phenomenon was observed to occur in the redshift of
quasars as well (Burbidge, 1968). Additional studies by
Arp (Arp 1987), Tifft (Tifft
1980,1995, 2003), Napier (Napier, 1997) and their
collaborators, conducted on larger sets of galaxies more widely
distributed, seem to validate these findings. Specifically, in a
limited trial on galaxies in the Virgo cluster, Bruce Guthrie and
William Napier reported that away from the dense central core of the
galaxy the redshifts were offset from each other in multiples of
about .
A similar phenomenon was observed to occur in the redshift of
quasars as well (Burbidge, 1968). Additional studies by
Arp (Arp 1987), Tifft (Tifft
1980,1995, 2003), Napier (Napier, 1997) and their
collaborators, conducted on larger sets of galaxies more widely
distributed, seem to validate these findings. Specifically, in a
limited trial on galaxies in the Virgo cluster, Bruce Guthrie and
William Napier reported that away from the dense central core of the
galaxy the redshifts were offset from each other in multiples of
about
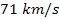 ,
and further reported a periodicity of about ,
and further reported a periodicity of about
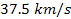 in the Coma Cluster (Guthrie & Napier, 1990). While
spiral galaxies were observed to display strong redshift periodicity,
no significant periodicity was found for two separate groups of
irregular galaxies. The increased accuracy achieved with the
introduction of the
in the Coma Cluster (Guthrie & Napier, 1990). While
spiral galaxies were observed to display strong redshift periodicity,
no significant periodicity was found for two separate groups of
irregular galaxies. The increased accuracy achieved with the
introduction of the
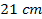 redshift measurements, and by correcting for the distortion effect
caused by the velocity of the Solar System relative to the cosmic
microwave background, led to the finding of additional redshift
velocities.
redshift measurements, and by correcting for the distortion effect
caused by the velocity of the Solar System relative to the cosmic
microwave background, led to the finding of additional redshift
velocities.
General relativity can provide redshift periodicity to the extent
reported only via a very particular distribution of matter. Such a
distribution is very unlikely to form spontaneously or to persist for
a long period of time. Consequently, it is quite difficult to
explain the observations of periodic redshift reported in a
considerable number of galaxies. Therefore, the existence of
redshift periodicity may require a paradigm shift, which can explain
the great deal of skepticism among the astronomical community as to
the merit of these findings. It has been suggested that the observed
periodicity, or ďquantization,Ē of galactic redshift may
be due to measurement or analysis error, due to coincidence, or due
to geometrical effects resulting from the correlated positions of
galaxies (Sepulveda, 1987).
The UG theory suggests the occurrence of redshift periodicity, or
quantization, resulting as a consequence of the tendency of ordinary
matter to accumulate within a distinct set of potential energy minima
created by the interaction between the galactic superheavy particles
and the ordinary matter of the orbiting gas or objects. Substituting
the distinct set of minima provided by equation 2-1-42,
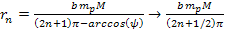 (for (for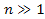 ),
in equation 10-1-1 yields ),
in equation 10-1-1 yields 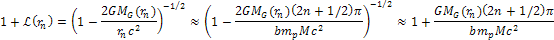
As
long as the vast majority of the mass of the galactic ordinary matter
is within the distance
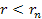 , ,
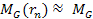 and
and
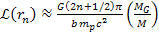 ,
thereby demonstrating a periodic redshift with a periodicity of ,
thereby demonstrating a periodic redshift with a periodicity of
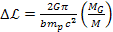 .1
However, as the UG theory violates the equivalence principle at
distances where rings or spiral arms occur, a UG analysis of redshift
periodicity should not rely on an equation of general relativity.
Therefore, an alternative approach is used, where the gravitational
redshift is derived from the equivalence of mass and energy under
special relativity. .1
However, as the UG theory violates the equivalence principle at
distances where rings or spiral arms occur, a UG analysis of redshift
periodicity should not rely on an equation of general relativity.
Therefore, an alternative approach is used, where the gravitational
redshift is derived from the equivalence of mass and energy under
special relativity.
In accordance with special relativity, the mass of the emitting
electron and the masses of protons in the nucleus of the same atom
deviate from their rest masses, due to their interactions with the
galactic superheavy particles and ordinary matter. The rest masses
of the electron and proton are denoted as
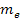 and
and
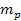 ,
and the masses of the interacting electron and proton are given by ,
and the masses of the interacting electron and proton are given by
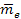 and
and
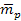 respectively. Radiation occurs when an electron transitions from a
higher energy quantum state to a lower energy quantum state, while
the energy of the emitted radiation is equal to the energy difference
between the two states. As the energy level of either atomic state
depends on the mass of the electron as well as on the masses of
protons, the emitted radiation energy measured by the distant
observer will deviate from the energy measured in the inertial rest
frame of an identical free atom.2
Therefore, the effective masses of the electron and the protons
deviate from their rest masses by a distinct set of values, resulting
in a clear periodic set of wavelengths, rather than continuous
radiation energies or wavelengths.
respectively. Radiation occurs when an electron transitions from a
higher energy quantum state to a lower energy quantum state, while
the energy of the emitted radiation is equal to the energy difference
between the two states. As the energy level of either atomic state
depends on the mass of the electron as well as on the masses of
protons, the emitted radiation energy measured by the distant
observer will deviate from the energy measured in the inertial rest
frame of an identical free atom.2
Therefore, the effective masses of the electron and the protons
deviate from their rest masses by a distinct set of values, resulting
in a clear periodic set of wavelengths, rather than continuous
radiation energies or wavelengths.
The following discussion will provide a more rigorous analytical
treatment of this phenomenon, specifically for the case of the
hydrogen
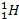 radiation lines. The hydrogen atom will be assumed to remain
isolated and unaffected by nearby objects, and to travel in a
circular orbit of radius
radiation lines. The hydrogen atom will be assumed to remain
isolated and unaffected by nearby objects, and to travel in a
circular orbit of radius
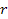 around a non-rotating galaxy center. The atomís orbital radius
around a non-rotating galaxy center. The atomís orbital radius
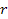 is assumed to lie beyond the zonal oscillation range of ordinary
matter of mass
is assumed to lie beyond the zonal oscillation range of ordinary
matter of mass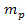 and all but the dominant SHP type. The dominant superheavy
particles of mass
and all but the dominant SHP type. The dominant superheavy
particles of mass
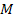 are assumed to be located and at rest at the center of the galaxy.
Note that the above assumptions are made for simplification, and do
not significantly restrict the generality of the discussion.
are assumed to be located and at rest at the center of the galaxy.
Note that the above assumptions are made for simplification, and do
not significantly restrict the generality of the discussion.
Whereas the radiation energy is given by
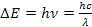 , where according to the law of conservation of energy,
, where according to the law of conservation of energy,
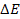 is the energy between the initial and final energy states of the
emitting electron, where
is the energy between the initial and final energy states of the
emitting electron, where
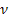 denotes the frequency of the radiation, and
denotes the frequency of the radiation, and
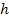 is Planckís constant.
is Planckís constant.
The following analysis is applied for the case of non-relativistic
atom velocity, where the energy of a free particle (an electron or
proton) of rest mass
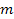 and velocity
and velocity
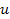 can be described accurately by the equation
can be described accurately by the equation
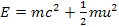 .
Initial studies of galactic redshift measured the redshift spectra
of the transitions between the various hydrogen ( .
Initial studies of galactic redshift measured the redshift spectra
of the transitions between the various hydrogen ( )
orbital levels. The electron orbital energy levels are given by3 )
orbital levels. The electron orbital energy levels are given by3 Equation
10-1-3a 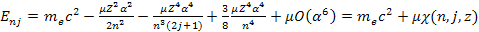
where
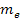 provides the rest mass of the electron,
provides the rest mass of the electron,
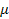 is the reduced mass of the electron-nucleus system in the inertial
rest frame of the emitting atom, and
is the reduced mass of the electron-nucleus system in the inertial
rest frame of the emitting atom, and
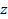 denotes the number of protons in the atom. The fine-structure
constant
denotes the number of protons in the atom. The fine-structure
constant
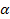 is defined as
is defined as
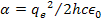 ,
where ,
where
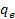 is the elementary charge,
is the elementary charge,
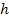 is Planckís constant,
is Planckís constant,
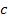 is the speed of light and
is the speed of light and
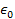 provides the vacuum permittivity. The quantum numbers of the
hydrogen quantum states are denoted as
provides the vacuum permittivity. The quantum numbers of the
hydrogen quantum states are denoted as
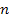 and
and
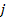 ,
where ,
where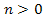 is a positive integer,
is a positive integer,
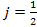 , ,
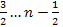 ,
and where ,
and where
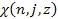 is defined as
is defined as Equation
10-1-3b 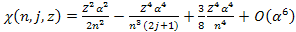
Note
that
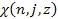 is independent of the masses of the protons and the electron. In the
case of the hydrogen atom
is independent of the masses of the protons and the electron. In the
case of the hydrogen atom
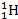 , ,
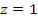 and
and
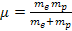 .
. The
wavelength of the radiation due to the electronís transition
from level
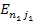 to level
to level
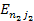 is subsequently given by
is subsequently given by Equation
10-1-4 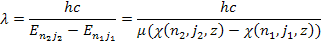
The
observer is assumed to be positioned at sufficient distance from the
galaxy to remain unaffected by its gravitational field. However, as
the galactic superheavy particles and ordinary matter are expected to
influence the masses of the electron and proton of the emitting
hydrogen atom, and therefore its reduced mass
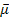 ,
the actual observed radiation is equal to ,
the actual observed radiation is equal to Equation
10-1-5 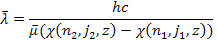
where
the redshift
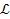 of the electronís orbital energy level is given by
of the electronís orbital energy level is given by Equation
10-1-6 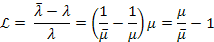
Defining
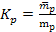 and
and
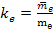 as the respective mass ratios of the proton and the electron, and
substituting μ,
as the respective mass ratios of the proton and the electron, and
substituting μ,
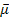 , ,
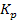 and and
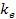 for the case of hydrogen
for the case of hydrogen
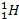 (
(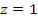 )
in equation 10-1-6 yields )
in equation 10-1-6 yields Equation
10-1-7
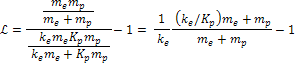
where
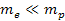 ,
and with the exception of extreme gravitational fields, ,
and with the exception of extreme gravitational fields, 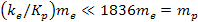 .
Therefore, .
Therefore,
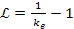 . .
Later studies of redshift periodicity started using the more
sensitive
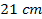 line for quantifying redshift. The
line for quantifying redshift. The
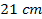 line is assumed to be created by the magnetic field induced by the
nucleus magnetic moment, resulting in the splitting of the triplet
and the singlet spin state energy levels (this energy split is also
called the hyperfine structure). The energy difference between the
triplet and the singlet spin states at the ground level of the
electron is given by
line is assumed to be created by the magnetic field induced by the
nucleus magnetic moment, resulting in the splitting of the triplet
and the singlet spin state energy levels (this energy split is also
called the hyperfine structure). The energy difference between the
triplet and the singlet spin states at the ground level of the
electron is given by
Equation
10-1-8 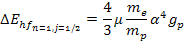
where
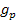 provides the reduced gyromagnetic ratio of the proton. Following the
same process, the
provides the reduced gyromagnetic ratio of the proton. Following the
same process, the
 redshift of the
redshift of the
 line is given by
line is given by
Equation
10-1-9 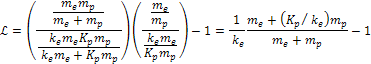
Assuming
that
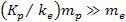 provides
provides
Equation
10-1-10a 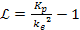
If,
in addition,
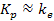 , ,
Equation
10-1-10b
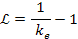
yielding
the same results as obtained for the case of the regular spectra of
the hydrogen atom.
As observed, and demonstrated by the theory developed in Chapter III,
the rotational velocities within and external to the galactic disk
relative to the galaxy center are of the order of hundreds of
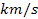 ,
too slow to cause any appreciable relativistic effects. This is also
true in the case of an observer located outside of the given galaxy
moving at a non-relativistic velocity relative to the galactic
center. Therefore, no velocity-related relativistic corrections are
required. However, according to Einsteinís mass equation for a
bonded electron-proton pair within a hydrogen atom ,
too slow to cause any appreciable relativistic effects. This is also
true in the case of an observer located outside of the given galaxy
moving at a non-relativistic velocity relative to the galactic
center. Therefore, no velocity-related relativistic corrections are
required. However, according to Einsteinís mass equation for a
bonded electron-proton pair within a hydrogen atom
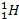 ,
viewed by a distant observer, the energy of the proton is given by ,
viewed by a distant observer, the energy of the proton is given by Equation
10-1-11
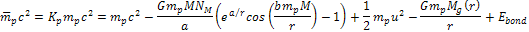
where
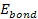 provides the overall bonding energy of the proton to the electron,
which must be negative,4
provides the overall bonding energy of the proton to the electron,
which must be negative,4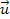 is the rotational velocity of the atom around the galaxy center, and
is the rotational velocity of the atom around the galaxy center, and
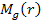 is the mass of the ordinary matter within a sphere of radius
is the mass of the ordinary matter within a sphere of radius
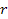 from the galaxy center. Additionally, the distribution of the
galactic ordinary matter around the center of the galaxy is assumed
to be spherically symmetric. Therefore,
from the galaxy center. Additionally, the distribution of the
galactic ordinary matter around the center of the galaxy is assumed
to be spherically symmetric. Therefore, Equation
10-1-12 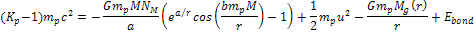
Over time, the rotating atom is likely to gravitate toward an orbital
radius near a potential energy minimum. Since the force applied on
the proton at any of the minima is zero, the orbit must shift
slightly from the minimum to allow the resultant gravitational force
to balance the centrifugal force. However, due to the steep slopes
of the potential energy at zonal indices
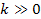 ,
the orbital radii at which the overall energy minima occur must be
very close to the radii where the overall potential energy of the
atom has a local minimum. Using equation 2-1-42 and restricting the
discussion to distances of ,
the orbital radii at which the overall energy minima occur must be
very close to the radii where the overall potential energy of the
atom has a local minimum. Using equation 2-1-42 and restricting the
discussion to distances of
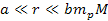 ,
where ,
where
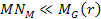 and
and
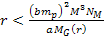 confines the potential energy minima of the proton or the atom to
confines the potential energy minima of the proton or the atom to
Equation
10-1-13a
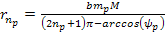
where
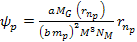 for
for
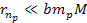 or
or
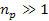 .
For sufficiently large .
For sufficiently large
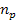 (and therefore, sufficiently small
(and therefore, sufficiently small
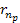 ), ),
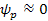 ,
and ,
and
Equation
10-1-13b 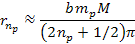
As
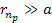 ,
equation 10-1-12 can be rearranged as follows: ,
equation 10-1-12 can be rearranged as follows: Equation
10-1-14 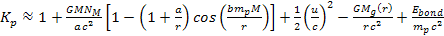
or 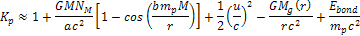
At
the range of interest
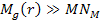 ,
substituting equation 10-1-13b in equation 10-1-14 provides a minimum
contour at ,
substituting equation 10-1-13b in equation 10-1-14 provides a minimum
contour at Equation
10-1-15 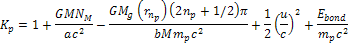
Similarly,
for the electron, Equation
10-1-16 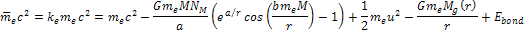
or Equation
10-1-17 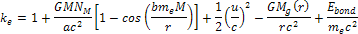
The
electron and the proton are bonded together, and thus travel at the
same velocity around the galaxy center. However, as the masses of
the electron and the proton differ substantially, the locations of
the potential energy minima of their interaction with a superheavy
particle of mass
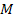 vary accordingly. Since the proton mass is over 1,836 times larger
than the mass of the electron, the atom is expected to reside near a
minimum of the proton-SHP interaction, which may be at substantial
distance from any minimum of the SHP-electron interaction. The
electron is therefore subject to the UG gravitational force, which
aims to draw the electron toward a UG potential energy minimum.
However, the electron is usually prevented from migrating toward this
minimum by its electromagnetic interaction with the proton. Hence,
for the case of a non-ionized hydrogen atom, the location of the
electron is given by
vary accordingly. Since the proton mass is over 1,836 times larger
than the mass of the electron, the atom is expected to reside near a
minimum of the proton-SHP interaction, which may be at substantial
distance from any minimum of the SHP-electron interaction. The
electron is therefore subject to the UG gravitational force, which
aims to draw the electron toward a UG potential energy minimum.
However, the electron is usually prevented from migrating toward this
minimum by its electromagnetic interaction with the proton. Hence,
for the case of a non-ionized hydrogen atom, the location of the
electron is given by
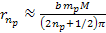 ,
rather than by ,
rather than by
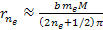 .
Substituting .
Substituting
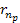 for
for
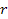 in equation 10-1-17 provides
in equation 10-1-17 provides
Equation
10-1-18
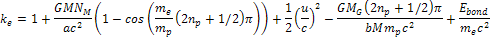
Using
equations 10-1-15 and 10-1-18 yields
Equation
10-1-19
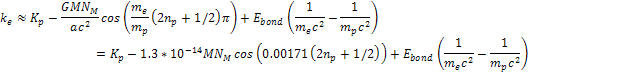
The
value of
 can be estimated from the rotational velocity of a typical spiral
galaxy, shown in section VI-3 of chapter VI to be equal to
can be estimated from the rotational velocity of a typical spiral
galaxy, shown in section VI-3 of chapter VI to be equal to
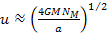 .
Thus, for a rotational velocity of .
Thus, for a rotational velocity of
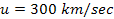 , ,
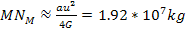 ,
which is far smaller than the overall galactic mass by a factor of
the order of at least ,
which is far smaller than the overall galactic mass by a factor of
the order of at least
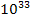 .
Therefore, .
Therefore, 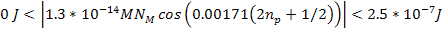 and
and
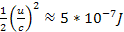 .
The magnitude of the term .
The magnitude of the term
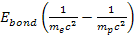 depends on the quantum state of the hydrogen atom. At the lowest
ground state,
depends on the quantum state of the hydrogen atom. At the lowest
ground state,
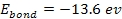 ,
and therefore ,
and therefore
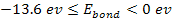 .
Consequently, .
Consequently,
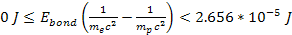 .
As long as the value of .
As long as the value of
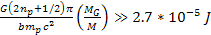 , ,
Equation
10-1-20
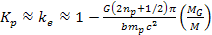 Substituting
equation 10-1-20 in equation 10-1-7 (or equation 10-1-10b) yields the
 shift for the hydrogen orbital lines (as well as for the
shift for the hydrogen orbital lines (as well as for the
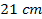 line), given by
line), given by Equation
10-1-21 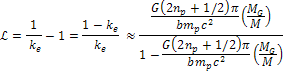
Therefore,
as long as
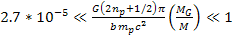 , ,
Equation
10-1-22 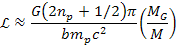
where
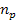 is an integer. Note that
is an integer. Note that
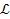 demonstrates periodic behavior with a periodicity of
demonstrates periodic behavior with a periodicity of Equation
10-1-23
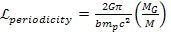
Note
that this intrinsic redshift is in addition to the expected redshift
contributed by the velocity of the galaxy relative to the observer.
Using equation 10-1-23, a redshift periodicity of
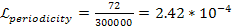 ,
which is equivalent to the reported redshift velocity of ,
which is equivalent to the reported redshift velocity of
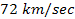 ,
leads to5 ,
leads to5 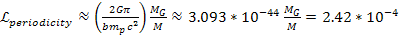 .
To achieve a periodicity of .
To achieve a periodicity of
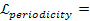 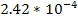 ,
the ratio of the overall galaxy mass and the dominating SHP mass ,
the ratio of the overall galaxy mass and the dominating SHP mass
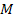 is given by
is given by
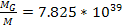 . .
Similar
calculations provide a value of
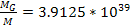 for the case of
for the case of
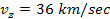 .
The above analysis, in addition to the fact that galaxies and
galactic clusters are observed to produce a distinct set of redshifts
with the same periodicity values shared by a significant number of
unrelated galaxies, suggests that the ratios .
The above analysis, in addition to the fact that galaxies and
galactic clusters are observed to produce a distinct set of redshifts
with the same periodicity values shared by a significant number of
unrelated galaxies, suggests that the ratios
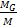 between the mass of the galactic center and the mass of the SHP tend
to assume specific values.
between the mass of the galactic center and the mass of the SHP tend
to assume specific values.
Section
X-2: Unified Gravitation and the Redshifts of Quasars
Quasars, or quasi-stellar objects, are astronomical objects that are
observed to emit highly redshifted radiation. According to the
standard model of cosmology, large redshifts are interpreted as
Doppler shifts, which lead to the following conclusions: The large
radiation redshifts observed in quasars indicates that they must
recede from us at very high speeds.
More than
200,000 quasars are known with redshifts ranging between
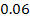 and
and
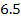 .
Applying Hubbleís law, which indicates that the velocity at
which various galaxies
are receding from Earth is proportional
to their distance from us, leads to the conclusion that the known
quasars are located between 790 million and 28 billion light years
away from us, with most calculated to be over three billion light
years away. .
Applying Hubbleís law, which indicates that the velocity at
which various galaxies
are receding from Earth is proportional
to their distance from us, leads to the conclusion that the known
quasars are located between 790 million and 28 billion light years
away from us, with most calculated to be over three billion light
years away.
As the
brightness of an object reduces proportionally to the square of its
distance from the observer, quasars are presumed to be extremely
luminous objects, radiating at rates that can exceed the output of
average galaxies.
The great
distances calculated between Earth and the known quasars lead to the
conclusion that quasars were much more common in the early universe.
The
assumption that substantial redshifts are due exclusively to Doppler
effectshas led to far-reaching
conclusions. This assumption was challenged by Halton Arpís
claim that the redshifts of quasars are not always an indication of
their distances or their ages, as currently believed (Arp,
1988). Arp contested that many quasars with otherwise high
redshifts can be linked to nearby objects of significantly lower
redshifts, and are therefore nearby.
According to special relativity, the masses of the electron
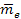 and the proton
and the proton
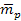 ,
as viewed by an external observer, cannot be negative, and therefore ,
as viewed by an external observer, cannot be negative, and therefore
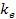 and
and
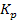 cannot be negative. In the case of sufficiently small values of
cannot be negative. In the case of sufficiently small values of
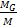 and
and
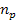 ,
the term ,
the term
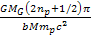 in equation 10-1-18 is negligible, and
in equation 10-1-18 is negligible, and
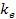 may assume values greater or less than
may assume values greater or less than
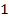 .
Thus, the objectís radiation frequency may either be
blueshifted or redshifted due to gravitation. On the other extreme,
in the case of .
Thus, the objectís radiation frequency may either be
blueshifted or redshifted due to gravitation. On the other extreme,
in the case of
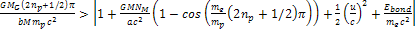 , ,
 of equation 10-1-18 assumes a negative value, which is forbidden by
special relativity. The physical meaning of this discrepancy is that
the given emitting atom lies within the horizon of the object, thus
its radiation is trapped in a black hole and cannot reach the
external observer.
of equation 10-1-18 assumes a negative value, which is forbidden by
special relativity. The physical meaning of this discrepancy is that
the given emitting atom lies within the horizon of the object, thus
its radiation is trapped in a black hole and cannot reach the
external observer.
According to equation 10-1-18, at distance ranges where
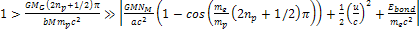 , , ,
and according to equation 10-1-7 (or 10-1-10b), the radiation
redshift due to the gravitational interaction is given by ,
and according to equation 10-1-7 (or 10-1-10b), the radiation
redshift due to the gravitational interaction is given by
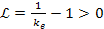 . .
The matter trapped by the object is expected to accumulate mainly in
vicinity of the potential energy minima. As noted above, at
sufficiently high
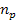 indices, the radiation is trapped within a black hole, and cannot
escape or be detected by the distant observer. Denote
indices, the radiation is trapped within a black hole, and cannot
escape or be detected by the distant observer. Denote
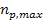 as the largest even integer index at which
as the largest even integer index at which
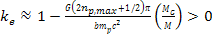 ,
where a minimum occurs.6As the potential energy slope is especially
steep near a black hole horizon, and as the minimum ,
where a minimum occurs.6As the potential energy slope is especially
steep near a black hole horizon, and as the minimum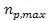 is the closest minimum to the horizon, the density of ordinary matter
in the vicinity of
is the closest minimum to the horizon, the density of ordinary matter
in the vicinity of
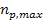 is likely to be significantly greater than the density anywhere
external to the horizon. Hence, the redshift associated with the
is likely to be significantly greater than the density anywhere
external to the horizon. Hence, the redshift associated with the
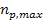 minimum may dominate the observed spectrum.7
minimum may dominate the observed spectrum.7
Following equation 10-1-21, in the case where
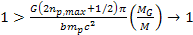 ,
the redshift of the observed radiation will approach infinity. In
cases where, in addition, ,
the redshift of the observed radiation will approach infinity. In
cases where, in addition,
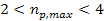 ,
most of the radiation emitted by the star is extremely redshifted, as
observed in quasars. Thus, the astronomical object is expected to
provide an intrinsic redshift that is significantly larger than the
Doppler redshift created by the objectís velocity relative to
the observer. Therefore, according to the theory of unified
gravitation, it is very possible that Arpís claim is in fact
true, and that at least some of the observed quasars may be
substantially closer, younger, smaller and less luminous than
currently believed. ,
most of the radiation emitted by the star is extremely redshifted, as
observed in quasars. Thus, the astronomical object is expected to
provide an intrinsic redshift that is significantly larger than the
Doppler redshift created by the objectís velocity relative to
the observer. Therefore, according to the theory of unified
gravitation, it is very possible that Arpís claim is in fact
true, and that at least some of the observed quasars may be
substantially closer, younger, smaller and less luminous than
currently believed.
1 Note that the much smaller UG
contribution of the electrons
was neglected. 2 The effect of the galactic
gravitational field on the mass of nucleons
and electrons is also
true for Newtonian gravitation
within special relativity,
with the exception that according to the UG theory, the atoms or
molecules of a galaxy are likely to be arranged in the vicinity of
distinct potential energy minima of the SHP-proton
pairs, rather than in the continuous distribution predicted by the
Newtonian theory. 3 For further reading, see Quantum
Field Theory by
Claude Itzykson and Jean-Bernard Zuber, Dover Publication, Inc.,
Mineola, New York, 2005. 4 The
value of 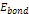 must be negative in order for the electron
to bond with the proton. In the general case, where the atom is
part of a molecule or a larger object,
must be negative in order for the electron
to bond with the proton. In the general case, where the atom is
part of a molecule or a larger object, 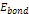 may denote the overall bonding energy of the proton to the object as
a whole. However, for simplicity, the current scenario deals with
an isolated hydrogen atom.
may denote the overall bonding energy of the proton to the object as
a whole. However, for simplicity, the current scenario deals with
an isolated hydrogen atom. 5 Note that the resultant
periodicity of the redshift 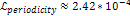 is indeed larger than the value
is indeed larger than the value 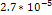 by a factor of
by a factor of 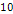 (even at the lowest
(even at the lowest 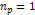 value) and less than
value) and less than 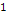 for all
for all 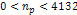 ,
fullfilling, within this range, the conditions required for the
assumption that ,
fullfilling, within this range, the conditions required for the
assumption that 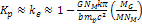 . . 6 Therefore, 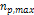 is the largest even integer where
is the largest even integer where 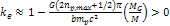 and where the minimum is not washed out by the contribution of the
objectís ordinary matter.
and where the minimum is not washed out by the contribution of the
objectís ordinary matter. 7
Note that the effect of the SHP
rotation as well as the Doppler effect
due to the relative speed between the distant galaxy and the
observer, or due to the velocity of the emitting atom relative to
the center of galaxy, are assumed in the present case to be
relatively small.
|



