Within our Solar System, the four inner planets have a solid surface,
and are referred to as terrestrial planets. These planets display no
planetary rings and few satellites. In contrast, the surfaces of the
four outer planets are non-solid and composed of gases.1
Gas planets are substantially more massive than terrestrial
planets, and display broad rings and extensive satellite systems.
The distinct differences in mass and radii between the terrestrial
and gas planets raise questions as to whether their composition and
structure are related to their size. A UG-based analysis will be
applied to examine the relationship between the mass of planets and
their resultant properties. It will be shown that under unified
gravitation, the formation of a substantial ring and satellite system
requires a planet of sufficient mass, and is mutually exclusive to
having a solid surface.
Section
IX-1: Planetary Ring and Satellite Systems of Terrestrial and
Gas Planets
The temperature and pressure within the cores of less massive
planets are less extreme, and are consequently expected to produce
less massive superheavy particles. The maximal zonal oscillation
ranges of the four terrestrial planets in the Solar System are thus
expected to extend to shorter distances than the maximal zonal
oscillation ranges of the four massive gas planets.
A mathematical formula relating the mass
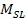 of the dominant SHP of a planet to the total planetary mass
of the dominant SHP of a planet to the total planetary mass
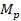 is unknown. In the present case, it is assumed that the mass of the
dominant SHP increases faster than the rate of growth of the radius
of the planet
is unknown. In the present case, it is assumed that the mass of the
dominant SHP increases faster than the rate of growth of the radius
of the planet
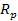 ,
which is roughly proportional to ,
which is roughly proportional to
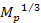 . . A common spherical macroscopic
object with a radius of the order of a few centimeters is too small
to produce superheavy particles
of a mass substantially larger than 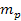 .
As the zonal oscillation range
of two ordinary particles of mass .
As the zonal oscillation range
of two ordinary particles of mass 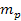 is of the order of
is of the order of 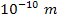 ,
the maximal zonal range
of the object is negligible relative to its radius. The mass of a
homogeneous object is proportional to the cube of its radius. The
assumption made here, that on average the mass of the dominant SHP
type of an object increases faster than the cube root of its mass,
implies that the mass of the dominant SHP
type increases faster than the radius of the object. Therefore,
beyond a certain radial value, the object’s maximal zonal
oscillation range,
which is proportional to ,
the maximal zonal range
of the object is negligible relative to its radius. The mass of a
homogeneous object is proportional to the cube of its radius. The
assumption made here, that on average the mass of the dominant SHP
type of an object increases faster than the cube root of its mass,
implies that the mass of the dominant SHP
type increases faster than the radius of the object. Therefore,
beyond a certain radial value, the object’s maximal zonal
oscillation range,
which is proportional to 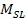 ,
is expected to exceed its radius. In such a case, some of the
potential energy minima of ordinary matter of mass ,
is expected to exceed its radius. In such a case, some of the
potential energy minima of ordinary matter of mass 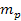 may occur above the surface of the object, creating areas of higher
matter density, or rings. In order for the length of the zonal
oscillation range of
the dominant superheavy particles
with ordinary matter to equal the radius of the object, the object’s
mass is expected to fall within the range between the mass of the
largest known object without a ring system
and the smallest object known to display a ring system. Hence, in
our Solar System this
mass value is expected to fall somewhere between the mass of the
planet Earth and the
mass of planet Uranus.
may occur above the surface of the object, creating areas of higher
matter density, or rings. In order for the length of the zonal
oscillation range of
the dominant superheavy particles
with ordinary matter to equal the radius of the object, the object’s
mass is expected to fall within the range between the mass of the
largest known object without a ring system
and the smallest object known to display a ring system. Hence, in
our Solar System this
mass value is expected to fall somewhere between the mass of the
planet Earth and the
mass of planet Uranus. As an example, assume that
within the range of masses covered by the eight Solar planets
between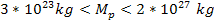 (see table 9.1), (see table 9.1),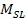 has an approximately linear dependency on the planet’s overall
mass (or
has an approximately linear dependency on the planet’s overall
mass (or
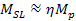 ).
For simplicity, the SHP velocities are assumed to be
non-relativistic and the influence of less dominant SHP groups will
not be taken into account. Applying the above simplifications, the
radius of the planet ).
For simplicity, the SHP velocities are assumed to be
non-relativistic and the influence of less dominant SHP groups will
not be taken into account. Applying the above simplifications, the
radius of the planet
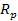 can be expressed by
can be expressed by
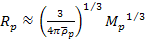 ,
where ,
where
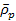 is defined as the average density of the planet. The external ring,
indexed
is defined as the average density of the planet. The external ring,
indexed
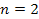 ,2
is given by ,2
is given by
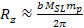 .
Therefore, rings may form when .
Therefore, rings may form when
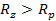 ,
or ,
or Equation
9-1-1 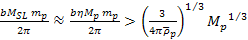
or Equation
9-1-2 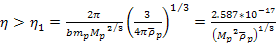
Table 9-1 provides the calculated values of
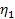 for all of the planets in the Solar System.
for all of the planets in the Solar System.
Given
that the four terrestrial planets do not display planetary rings,
while the four gas giants maintain rings, the value of
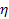 lies somewhere within the range
lies somewhere within the range
Equation
9-1-3 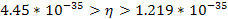
Note, however, that the assumption of linearity
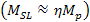 was used only as an example. In the case where the relation between
was used only as an example. In the case where the relation between
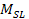 and and
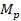 is non-linear, as long as
is non-linear, as long as
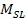 increases consistently at a higher rate than
increases consistently at a higher rate than
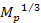 ,
ring systems will occur exclusively in objects of a mass greater than
some threshold mass value. Taking the above discussion one step
further, when the zonal oscillations of the planetary superheavy
particles with ordinary matter extend beyond the Roche limit of a
planet, the rings located external to this limit are likely to
coalesce to produce satellites. As discussed, this process can occur
in planets of substantial mass, where the oscillation range of the
SHP- ,
ring systems will occur exclusively in objects of a mass greater than
some threshold mass value. Taking the above discussion one step
further, when the zonal oscillations of the planetary superheavy
particles with ordinary matter extend beyond the Roche limit of a
planet, the rings located external to this limit are likely to
coalesce to produce satellites. As discussed, this process can occur
in planets of substantial mass, where the oscillation range of the
SHP-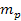 interaction exceeds the radii of the planets. This process may
consequently account for the large number of satellites observed to
encircle the four gas giants, and may further explain why
terrestrial planets, which do not generate ring systems at which
matter can accumulate and coalesce, have few satellites. According
to unified gravitation, the moons of terrestrial planets are
theorized to have been captured into orbit by the gravitational pull
of their parent planet. These captured satellites may have
originated external to the planetary system, or may have formed in
tandem with their parent planet, in an adjacent orbit. In keeping
with this scenario, Earth and its moon may have formed within
virtually the same ring of the Sun, at two local minima generated by
the “interference pattern” of various solar SHP groups.3
As their masses increased, the gravitational interaction between the
Earth and the moon became sufficiently strong and they began to orbit
around each other, as well as around the Sun. Such a scenario may
provide one or two satellites, however not the large quantity of
satellites observed to orbit the giant gas planets.
interaction exceeds the radii of the planets. This process may
consequently account for the large number of satellites observed to
encircle the four gas giants, and may further explain why
terrestrial planets, which do not generate ring systems at which
matter can accumulate and coalesce, have few satellites. According
to unified gravitation, the moons of terrestrial planets are
theorized to have been captured into orbit by the gravitational pull
of their parent planet. These captured satellites may have
originated external to the planetary system, or may have formed in
tandem with their parent planet, in an adjacent orbit. In keeping
with this scenario, Earth and its moon may have formed within
virtually the same ring of the Sun, at two local minima generated by
the “interference pattern” of various solar SHP groups.3
As their masses increased, the gravitational interaction between the
Earth and the moon became sufficiently strong and they began to orbit
around each other, as well as around the Sun. Such a scenario may
provide one or two satellites, however not the large quantity of
satellites observed to orbit the giant gas planets.
Table
9-1 | Planet | Density (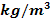 ) )
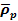 | Mass
(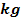 ) )
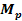 | 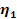 | | Jupiter | 1,326 | 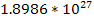 | 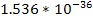 | | Saturn | 687.3 | 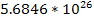 | 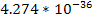 | | Uranus | 1,270 | 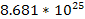 |  | | Neptune | 1,638 | 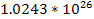 | 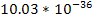 | | Earth | 5,515 | 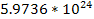 | 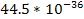 | | Mars | 3,934 | 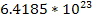 | 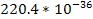 | | Venus | 5,204 | 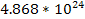 | 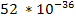 | | Mercury | 5,427 | 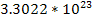 | 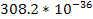 |
Section
IX-2: Unified Gravitation and the Surface Structure of Gas and
Terrestrial Planets
The UG explanation for the composition of planets, specifically the
observation that the larger solar planets consist of non-solid
surfaces, can be examined in the context of the discussion of the
previous section. The existence of a ring system indicates that the
zonal oscillation range generated by the planetary superheavy
particles exceeds the radius of the planet. Therefore, the rapid
oscillations of the potential energy create strong tidal forces that
extend beyond the planetary surface and prevent surface layers of
gases from transitioning to solid form. In smaller planets, the
zonal oscillation range of the dominant superheavy particles is
expected to terminate well below the planetary surface. Hence, the
tidal forces applied on a planet’s surface by its superheavy
particles are small, allowing ordinary matter on the planetary
surface to solidify.
Section IX-3: The Composition of Earth’s Core
As suggested in the third chapter, superheavy particles are generated
deep within the cores of astronomical objects (probably as pairs of
superheavy particles and anti-particles) with sufficient initial
kinetic energy and momentum to allow for their ejection from the
central core, yet not adequately large to set them free.
Consequently, SHPs enter into approximately circular orbits of radii
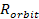 around the central core, where the zonal oscillation range of the
superheavy particles is given by
around the central core, where the zonal oscillation range of the
superheavy particles is given by
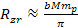 .
Ordinary matter is likely to coalesce in regions external to the
zonal oscillation range of massive superheavy particles.
Consequently, as long as .
Ordinary matter is likely to coalesce in regions external to the
zonal oscillation range of massive superheavy particles.
Consequently, as long as
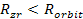 and
and
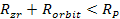 ,
the inner core and the outer layers of the planet do not fall within
the zonal oscillation range of large SHPs and are thus expected to
solidify.4
The middle section of the planet, between ,
the inner core and the outer layers of the planet do not fall within
the zonal oscillation range of large SHPs and are thus expected to
solidify.4
The middle section of the planet, between
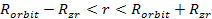 ,
is located within the zonal oscillation range of large SHPs, and is
thus expected to remain non-solid or viscous. Looking into the
composition of our planet, the radius of Earth’s solid inner
core is ,
is located within the zonal oscillation range of large SHPs, and is
thus expected to remain non-solid or viscous. Looking into the
composition of our planet, the radius of Earth’s solid inner
core is
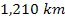 and the radius of its outer liquid core lies between
and the radius of its outer liquid core lies between
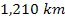 and
and
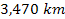 from the planetary center. Above the liquid layers of the core lies
the highly viscous mantle between
from the planetary center. Above the liquid layers of the core lies
the highly viscous mantle between
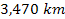 and
and
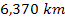 from the center of Earth,5
and an additional
from the center of Earth,5
and an additional
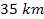 of a solid outer crust. Using these values, the mass and orbital
radii of the Earth’s dominant superheavy particles can be
estimated, where
of a solid outer crust. Using these values, the mass and orbital
radii of the Earth’s dominant superheavy particles can be
estimated, where
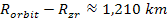 and
and
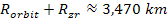 provide
provide
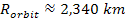 and
and
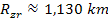 ,
leading to ,
leading to
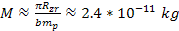 .
Therefore, the mass of the dominant SHP within the Earth is expected
to equal approximately .
Therefore, the mass of the dominant SHP within the Earth is expected
to equal approximately
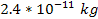 .
Note that Earth may contain larger superheavy particles as well, but
in quantities that are too minor to be noticed. Further note that
based on unified gravitation, the outer core is not necessarily in a
liquid or gas form. Rather, the outer core is more likely to be
composed of layers of high matter density separated by layers of
significantly lower density, where the layered structures rotate at
lower angular velocities than the SHP groups, and are thus subjected
to rotating density waves generated by the SHPs. .
Note that Earth may contain larger superheavy particles as well, but
in quantities that are too minor to be noticed. Further note that
based on unified gravitation, the outer core is not necessarily in a
liquid or gas form. Rather, the outer core is more likely to be
composed of layers of high matter density separated by layers of
significantly lower density, where the layered structures rotate at
lower angular velocities than the SHP groups, and are thus subjected
to rotating density waves generated by the SHPs.
Section
IX-4: The Creation of Planetary, Stellar and Galactic Magnetic
Fields via Unified Gravitation
The
Sun, the Earth and the other solar planets are known to have magnetic
fields, a phenomenon described by Einstein as being one of the great
unsolved problems facing modern physics. The exact cause for the
observed magnetic fields remains unknown. Earth’s magnetic
field is presently believed to result from electric currents in its
liquid outer core, however the origin of these currents is not
well-understood.
As
discussed in Chapter VIII, at distances below
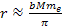 ,
free electrons tend to gravitate toward their minima contours at
about ,
free electrons tend to gravitate toward their minima contours at
about
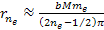 ,
while below ,
while below
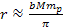 ,
protons and ions (as well as neutral atoms, neutrons and molecules)
tend to gravitate toward the minima of the ordinary matter ,
protons and ions (as well as neutral atoms, neutrons and molecules)
tend to gravitate toward the minima of the ordinary matter
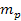 ,
at about ,
at about
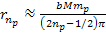 .
Since .
Since
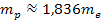 ,
there are 1,836 proton-SHP minima between any two successive
electron-SHP minima. ,
there are 1,836 proton-SHP minima between any two successive
electron-SHP minima. Ionization
may be caused by the UG gravitational force (as explained in Chapter
VIII), by radiation (electromagnetic fields), or thermally (through
collisions or radiation). In any case, if a free electron and an ion
are within the electron-SHP zonal oscillation range, each will
gravitate toward its nearest respective minimum and enter into an
orbit. Each rotating charge is expected to generate a magnetic field
of Equation
9-4-1
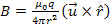
The total amount of negative and positive charges must be equal in
order to maintain overall neutrality. According to the current
paradigm (based on the electromagnetic/Newtonian scenario), the
lighter electrons are expected to reach substantially higher
velocities than the heavier ions, and the magnetic field generated by
the ions is thus negligible. However, both thermal and
radiation-driven ionization are random by nature. Substantially high
temperatures are required for the generation of the massive
ionization needed for the creation of the measured magnetic fields.
At such high temperatures, the spatial and velocity distributions of
the free electrons are expected to be entirely random. Therefore,
the magnetic fields produced by the various electrons should cancel
out, and no substantial global magnetic field should be observed.
According
to the UG scenario, ions and protons are
organized in a distinct set of orbits within the SHP-proton
zonal oscillation range, dictated by an orderly
set of minima. The same is true for the electrons
within the SHP-electron
oscillation range.6
The velocities of the nearby electrons and
protons (or ions) are determined by the
rotational velocity of the central core at very
short distances, or may be given by equation 6-5, 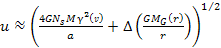 ,
at larger distances. In either case, the velocity of the charged
particles is independent of their masses.
Consequently, in close proximity to the SHP
groups, ions and protons travel at velocities
that are comparable to the velocities of the electrons
and rotate in the same direction within the same orbital plane, as
dictated by the rotation of the SHP groups.
Since all charges rotate in the same direction, the magnetic fields
generated by the rotating positive charges point in a single
direction, opposite to the direction of the contribution of the
rotating negative charges.7
However, since the positive and negative charges are distributed in
different sets of orbits, they are not likely to recombine, and their
magnetic fields cannot entirely cancel each other out. As a result,
a global planetary, stellar or galactic magnetic field may be
generated. ,
at larger distances. In either case, the velocity of the charged
particles is independent of their masses.
Consequently, in close proximity to the SHP
groups, ions and protons travel at velocities
that are comparable to the velocities of the electrons
and rotate in the same direction within the same orbital plane, as
dictated by the rotation of the SHP groups.
Since all charges rotate in the same direction, the magnetic fields
generated by the rotating positive charges point in a single
direction, opposite to the direction of the contribution of the
rotating negative charges.7
However, since the positive and negative charges are distributed in
different sets of orbits, they are not likely to recombine, and their
magnetic fields cannot entirely cancel each other out. As a result,
a global planetary, stellar or galactic magnetic field may be
generated. In the specific case of Earth’s
magnetic field, the orbits of the dominant SHP
groups were estimated in the previous section to reside within
Earth’s outer core. As the SHPs rotate
around the center of Earth, they ionize nearby atoms and organize the
free ions and electrons into separate orbits,
therefore creating separate currents of ions and electrons
within the outer core. These currents generate Earth’s magnetic
field via a dynamo effect, in accordance with current theory.
Section
IX-5: The Solar Corona
Located above the Sun’s transition region, the
solar corona starts at about 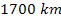 above the photosphere and extends out into space
without a well-defined outer boundary. The corona’s energy
output is nearly
above the photosphere and extends out into space
without a well-defined outer boundary. The corona’s energy
output is nearly 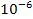 of that of the photosphere. However, whereas the average
temperature of the Sun’s photosphere is
of that of the photosphere. However, whereas the average
temperature of the Sun’s photosphere is 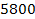 kelvin, the corona’s temperature is between one and three
million Kelvin. The higher temperature of the corona rules out
simple conduction of heat as its heating mechanism, and the exact
process by which the corona is heated is still subject to debate.
kelvin, the corona’s temperature is between one and three
million Kelvin. The higher temperature of the corona rules out
simple conduction of heat as its heating mechanism, and the exact
process by which the corona is heated is still subject to debate.
A
possible UG-driven theory proposes that the solar corona is located
at the external minimum layer of a dominant SHP
at 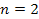 ,
while the higher minima of ,
while the higher minima of 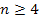 are positioned deep under the surface of the Sun, and are thus
undetectable. As a result, a significantly higher density of matter
is expected at the vicinity of the dominant SHP-
are positioned deep under the surface of the Sun, and are thus
undetectable. As a result, a significantly higher density of matter
is expected at the vicinity of the dominant SHP-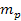 minimum
minimum 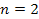 ,
causing a dramatic elevation in temperature. Consequently,
superheavy particles
may be generated, and subsequently decay, at this minimum. Prior to
their decay, these SHPs create a series of minima at which ordinary
matter may concentrate to form the observed c (see figure 9.1).8
The coronal loops may be generated by one or more superheavy
particles
of the same or of different masses located at varying distances from
each other, thereby different loops may demonstrate entirely
different structures. As new SHPs are created and then decay,
coronal loops are expected to be transient. Figure 9-1 displays an
observed coronal loop that appears almost identical in structure to a
single lobe of the hourglass nebula
MyCn18 discussed in chapter IV (a single lobe, since only the part of
the overall structure that is located above the surface of the Sun is
visible), suggesting that this particular coronal loop may also be
generated by binary superheavy particles
located at the ,
causing a dramatic elevation in temperature. Consequently,
superheavy particles
may be generated, and subsequently decay, at this minimum. Prior to
their decay, these SHPs create a series of minima at which ordinary
matter may concentrate to form the observed c (see figure 9.1).8
The coronal loops may be generated by one or more superheavy
particles
of the same or of different masses located at varying distances from
each other, thereby different loops may demonstrate entirely
different structures. As new SHPs are created and then decay,
coronal loops are expected to be transient. Figure 9-1 displays an
observed coronal loop that appears almost identical in structure to a
single lobe of the hourglass nebula
MyCn18 discussed in chapter IV (a single lobe, since only the part of
the overall structure that is located above the surface of the Sun is
visible), suggesting that this particular coronal loop may also be
generated by binary superheavy particles
located at the 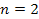 minimum.
minimum. 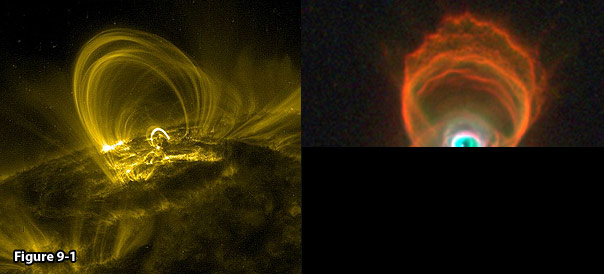
Figure
9-1: Coronal
loops, image credit: TRACE
NASA;
http://trace.lmsal.com/POD/TRACEpodarchive24.html.
In the fourth chapter, the hourglass structure of MyCn 18
was produced using a simple UG model of binary of stationary SHP
groups. The resemblance between the structure of the coronal loop in
figure 9-1 and a single lobe of MyCn 18 suggest that both structures
may be governed by similar interactions.
1 Note that planetary gases may
become compressed into liquids or solids further in toward their
interiors. 2
As previously discussed, the external ring between the 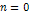 minimum
and the minimum
and the 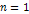 maximum demonstrates negligible amplitude and thus can be
discounted. Note that this external ring may be observed as an
extremely faint and diffused ring.
maximum demonstrates negligible amplitude and thus can be
discounted. Note that this external ring may be observed as an
extremely faint and diffused ring. 3
For additional information, see figure 4-2 and footnote 63 in
Chapter IV. Current theory holds that the Moon
was created by a collision between Earth
and an external body. 4 Note that the center of the
planet may be sufficiently massive to eliminate zonal oscillations,
even in cases where the center is located within the oscillation
range of the orbiting
superheavy particles. In
such a case, we can only rely on 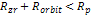 .
Therefore, the mass of the dominant SHP
may be larger than the mass calculated in this section. .
Therefore, the mass of the dominant SHP
may be larger than the mass calculated in this section. 5 According to this model, the
mantle lies on a downward slope of the potential beyond 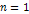 at
at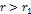 .
Therefore, the inner part of the mantle is almost liquid, whereas
the outer mantle becomes increasingly solid. .
Therefore, the inner part of the mantle is almost liquid, whereas
the outer mantle becomes increasingly solid. 6
Note that the ionization
can be initiated not only by external radiation and a thermal
process, but also by gravitational (UG) ionization. In either case,
the ions and the electrons
which are within their oscillation range
with the SHPs, gravitated toward a potential energy minimum. 7 In the present case, positive
charges refer to ions and protons,
and negative charges refer to electrons. 8 The
ionization
and the strong magnetic fields
created by the coronal SHPs may also play some role in determining
the morphology
of the coronal loops.
|



